応用数学（微分方程式、フーリエ、複素解析、グラフ理論）の記事まとめ

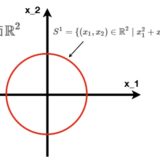
微分方程式、フーリエ解析、複素解析、グラフ理論などの応用数学についての記事をまとめて紹介します。

微積分学と線形代数学を学部1年で学んだ上で、これらの内容の一部分を学部2-3年で学ぶことが多いでしょう。どの分野を重点的に学ぶかは、専攻分野次第です。

常微分方程式

常微分方程式（ordinary differential equation,ODE）は、1つの変数に関する微分を含んだ関数に関する方程式です。物理、化学、生物学、経済学をはじめとして、常微分方程式を使った数理モデルは広く利用されています。特に1階、2階の線形方程式の解き方が基本的です。

物理ではべき級数解法を、工学ではラプラス変換を学ぶことが多いでしょう。

数理モデル

なぜ中学数学で関数を学ぶか：数理モデルの考え方

なぜ中学・高校数学を学ぶのか 数理モデルとしての微分方程式

人類は必ず食糧問題に直面する？ マルサスの法則と微分方程式

ニュートンの冷却法則とは：意味と解き方

空気抵抗があるときの落下運動、終端速度とは：運動方程式を解く

水の流出現象、トリチェリの法則とは：微分方程式を解く

サイン、コサインは何の役に立つ？ バネの振動と三角関数

おもりバネの運動：単振動の運動方程式、微分方程式の解き方

おもりバネダンパ系：減衰振動の運動方程式、微分方程式の解き方

RL直列回路の微分方程式の立て方、電流の求め方、過渡現象

RLC直列回路の微分方程式の立て方、電流の求め方、減衰振動

梁の変形：たわみ曲線・弾性曲線を微分方程式を解いて求める

食う-食われるの数学：捕食者-被食者モデル（ロトカ・ヴォルテラ方程式）とは？

漸化式と微分方程式は似ている：簡単な例で解説

線形微分方程式

不定積分と定積分をなぜ学ぶか 微分方程式の一般解と特殊解

対数logの外し方、外せる条件と対数関数の性質

微分方程式の解でなぜ指数関数（exp・ネイピア数）が現れるか

常微分方程式の変数分離形とは：証明と注意点（特異解）

1階線形微分方程式の解き方と証明：積分因子、定数変化法

ロジスティック方程式の解き方：ベルヌーイの微分方程式

同次形の2階線形微分方程式の解き方、学ぶ意味：熱方程式への応用を例に

線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか

ロンスキアンによる線形独立性の判定、証明

オイラー・コーシーの微分方程式の解き方、例

非同次の2階線形微分方程式の解き方、未定係数法：強制振動を例に

線形常微分方程式を行列で解く：行列の指数関数を解説

完備性とは：無理数、微分方程式の解の近似を例に

微分方程式の解の存在と一意性が成り立たない例

べき級数解法、特殊関数、ストゥルム・リウビル型

ストゥルム・リウビル型微分方程式の発見：熱方程式から

関数の重み付き内積とは：内積の定義を満たすことの証明

ストゥルム・リウビル型微分方程式における固有関数の直交性の証明

直交多項式とは：ルジャンドル多項式、微分方程式を例に

微分方程式のべき級数解法とは：指数関数、三角関数を例に

ルジャンドルの微分方程式、多項式とは：べき級数法による求め方

フロベニウスの方法とは：ベッセル方程式、第一種ベッセル関数を例に

第一種ベッセル関数のガンマ関数による表示式

フロベニウスの方法：次数0の第二種ベッセル関数の求め方

ラプラス変換

ラプラス変換とは：定義と微分方程式への応用

微分（導関数）のラプラス変換の求め方、証明

単位ステップ関数とは、ラプラス変換と微分方程式への応用

ラプラス変換の第一シフト定理（s推移法則）とは、証明、応用例

デルタ関数、超関数とは：ラプラス変換、微分方程式への応用

畳み込み（合成積）とは：ラプラス変換の性質と導出

ヴォルテラの積分方程式とは、ラプラス変換による解き方

ラプラス変換の微分とは：証明と応用

ラゲールの方程式、多項式とは：ラプラス変換による解法

おもり2つのバネの運動方程式（連成振動）：ラプラス変換による解き方

力学系理論、定性的理論

惑星の運動は数学的に「解けない」？　多体問題から力学系理論へ

方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門

線形微分方程式の解の安定性は「固有値」を調べればわかる

微分方程式の安定性を調べる「線形化」の方法とは？

安定性を判別するリヤプノフ関数の方法とは？

1次元の線形力学系とは：相図の書き方、安定性

2次元線形力学系の平衡解の分類：ノード（結節点）とは

2次元線形力学系の平衡解の分類：サドル（鞍点）とは

2次元線形力学系の平衡解の分類：スパイラル（渦状点）とは

減衰振り子の力学系：平衡解の安定性を線形化して調べる

ロトカ・ヴォルテラ方程式の平衡解の安定性、解曲線の求め方

高階常微分方程式の連立形への書き換えについて

非線形バネの方程式とは：平衡解の安定性を調べる

ファンデルポール方程式、リミットサイクルとは

極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理

不変集合、安定・不安定・中心多様体とは何か？

力学系の分岐理論、分岐図を簡単な例で解説

力学系の構造安定性について簡単に紹介

カオス理論、バタフライ・エフェクトとは何か？ ローレンツ・アトラクターを例に

カオス現象のわかりやすい具体例を視覚的に見る

フーリエ解析・偏微分方程式

常微分方程式は1次元的な問題を扱いますが、2次元や3次元的な問題を扱うと、偏微分を含んだ関数に関する方程式、偏微分方程式（partial differential equation, PDE）になります。偏微分方程式の中では、熱伝導方程式、波動方程式、ラプラス方程式が基本的です。

フーリエ解析（Fourier analysis）は、与えられた関数を三角関数の和：フーリエ級数として近似することについての分野です。もともとは熱方程式の解を求める中で生まれた手法ですが、電気や通信の分野などでも応用されています。

数理モデル

なぜ偏微分を学ぶ？ フーリエの熱伝導方程式を例に

なぜ重積分を学ぶ？ 熱伝導方程式の導出を例に

花粉の広がりを数式で予測する、拡散方程式とは

波の重ね合わせの原理はなぜ成り立つ？ 波動方程式入門

1次元の波動方程式（弦の振動）の導出：運動方程式から

偏微分方程式とは：2階線形の重要な例（ラプラス、熱、波動）

2階偏微分方程式の分類：楕円型、放物型、双曲型とは

生き物の模様は数式で決まる？ チューリング・パターンとは

フーリエ級数

線形代数の応用：関数の「空間・基底・内積」を使ったフーリエ級数展開

三角関数の直交性とは：フーリエ級数展開と関数空間の内積

フーリエ係数に関するオイラーの公式の導出

フーリエサイン・コサイン級数とディリクレ・ノイマン境界条件の関係

偶関数・奇関数のフーリエ級数、係数の求め方、証明

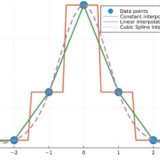
矩形波とは：フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数

のこぎり波とは：フーリエ級数展開の求め方

三角波とは：フーリエ級数展開の求め方

絶対サイン波|sin x|とは：フーリエ級数展開の求め方

フーリエ級数の収束条件：L^2収束、一様収束、不連続点での値

フーリエ係数の最良性とは：証明、ベッセルの不等式、パーセバルの等式

フーリエ係数の減衰：リーマン・ルベーグの補題とは、証明

一般フーリエ級数とは：フーリエ・ルジャンドル級数、フーリエ・ベッセル級数を例に

偏微分方程式の解き方

移流方程式（輸送方程式）とその解き方を解説

1次元の非同次の移流方程式の解き方：特性曲線法

偏微分方程式が変数分離法によって解けるのはなぜか

熱方程式の解き方：変数分離法、フーリエ級数展開（1次元、有界領域）

関数項級数の一様収束、Mテストとは：熱方程式への応用

熱方程式の解き方：フーリエ変換（全空間、N次元）

移流拡散方程式、その解き方：熱方程式への関数変換

合成関数の偏微分、チェインルールとは：波動方程式を例に

1次元波動方程式の解き方：変数分離法、フーリエ級数展開

1次元波動方程式の解：ダランベールの公式の証明、導出

1次元のラプラス方程式の解き方

1次元のポアソン方程式の解き方：定数変化法

1次元ラプラシアンの固有値問題の解き方、固有関数とは

2次元長方形領域でのラプラス方程式の解き方

チェインルール：2次元極座標でのラプラシアンを例に

円環領域におけるポテンシャル：2次元ラプラス方程式の解き方

ラプラシアンが回転不変であること：2次元での証明

なぜルベーグ積分を学ぶのか 偏微分方程式への応用の観点から

複素解析

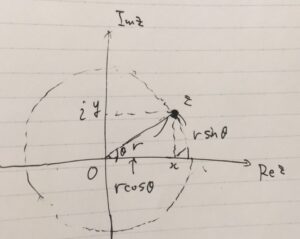
複素解析（complex analysis）は、複素変数の関数の微積分などに関する分野です。日本では関数論と呼ばれることも。

オイラーの公式によって、三角関数の情報を指数関数として簡単にまとめることができます。これはフーリエ解析、回路や通信の分野で応用されるものです。複素積分や留数の理論は、難しい実積分の計算を可能にし、ラプラス変換とも関係します。

調和関数、等角写像の理論、ポテンシャル論は、実平面のポテンシャルの問題を複素平面の問題に持ち込み、流体力学など流れの分析に役立ちます。

複素関数、級数、微分

複素数の積＝回転行列の積：対応関係を解説

複素数で普通の順序・不等号・大小関係を考えないのはなぜか

複素べき級数、収束半径とは：指数・三角関数を例に

べき級数の収束発散が円盤によって分かれること：収束半径の性質

オイラーの公式、極形式、ド・モアブルの定理とは：複素指数関数、三角関数の性質

複素関数の主値、多価関数・一価関数とは：平方根、ルートを例に

複素対数関数の主値Log zとは、計算例

複素数の複素数乗、べき乗・指数関数の主値とは何か、計算例

複素微分、正則関数・解析関数とは：具体例をもとに

複素積分、留数

複素関数の線積分とは：具体例をもとに

コーシーの積分定理とは：積分路の変形、証明

ガウス関数のフーリエ変換の計算法：コーシーの積分定理

コーシーの積分公式とは、計算例と応用（無限回微分可能、コーシーの不等式）

複素解析におけるリウビルの定理とは：例と証明

代数学の基本定理とは：リウビルの定理による証明

複素関数のテイラー展開（べき級数展開）とは、証明

ローラン展開とは：求め方、孤立特異点の分類（極、除去可能特異点、真性特異点）

留数、留数定理とは：定義と証明、計算例

極における留数の公式、計算例、位数の求め方

三角関数の有理関数の積分：留数定理による計算

調和関数、等角写像、ポテンシャル論

共役調和関数とは：定義と例

複素ポテンシャルとは：円環領域を例に

等角写像とは、性質：z^2を例に

単位円盤を単位円盤に写す線形分数変換とは、例

中心のずれた円環領域におけるポテンシャルの求め方：線形分数変換の応用

流体の複素ポテンシャル、速度ポテンシャル、流れ関数、流線とは

複素解析における最大値の原理とは：例、注意点

複素解析におけるポアソンの積分公式とは、ポアソン核との関連

複素解析・調和関数に関する平均値の性質とは、例と証明

グラフ理論

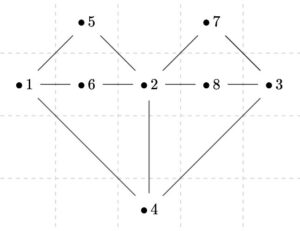
グラフ理論（graph theory）におけるグラフは、鉄道の路線図や、電気の回路、コンピュータのネットワークを表し、分析するために使われます。いわゆる「関数のグラフ」とは別物です。

一筆書きの問題、オイラーの多面体定理、四色問題、巡回セールスマン問題などが有名ですね。

微分方程式を使ったモデルは連続的ですが、これに対してグラフを使ったモデルは離散的です。離散的な対象を扱う数学は、離散数学（discrete mathematics）とも呼ばれています。

なぜ線形代数を学ぶ？ Googleのページランクに使われている固有値・固有ベクトルの考え方

グラフ理論入門：グラフとは、グラフの同型

グラフ理論における次数、握手の補題とは

グラフ理論における経路、連結性とは？

一筆書きができる条件、オイラーグラフとは

グラフ理論における木とは、判定法、オイラーの公式

平面グラフ、面とは何か、クラトフスキーの定理

グラフ理論におけるオイラーの公式とは、証明、多面体定理

地図の塗り分け、グラフの彩色問題、四色定理とは何か

グラフ理論における2部グラフ、マッチング、結婚定理とは

グラフ理論における全域木とは？ その求め方

重み付きグラフ、最小全域木の問題とは？ クラスカル法による解き方

数理最適化、線形計画法

執筆中。

線形代数の応用：線形計画法～輸送コストの最小化を例に

数値解析、数値線形代数

執筆中。

オイラー法：常微分方程式をPythonで解く原理を解説

ルンゲ＝クッタ法：常微分方程式をPythonで解く原理を解説

確率、統計、データ分析

執筆中。

確率の定義「場合の数」とは何か：結果の個数である

高校数学から始める公理的確率論：標本空間、事象、確率とは

Pythonで統計量関数（平均、中央値、分散、相関係数）を作り、可視化しよう

統計的推測の基礎：大数の法則をわかりやすく解説

確率・統計における用語「分布」について整理する

教科書

Advanced Engineering Mathematics

posted with AmaQuick at 2022.02.10

Kreyszig, Erwin(著)
John Wiley & Sons Inc (2011-05-03T00:00:01Z)

￥7,964

Amazon.co.jpで詳細を見る