どうも、木村(@kimu3_slime)です。
今回は、2次元線形力学系の平衡点の分類:ノード(結節点)とは何か紹介します。
2次元の線形力学系とは
2次元(平面)の線形力学系とは、\(x(t)=(x_1(t),x_2(t))\)、\(A\)をサイズ\(2,2\)の行列として
\[ \begin{aligned}\frac{dx}{dt}= Ax\end{aligned} \]
と表される連立常微分方程式のことです。
\(Ax=0\)を満たす解、つまり\(x=0\)を平衡解(定常解、固定点、臨界点)と呼びます。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門、線形微分方程式の解の安定性は「固有値」を調べればわかる、1次元の線形力学系とは:相図の書き方、安定性
2次元の力学系では、平衡解はおよそ3つに分類されます。
- ノード(結節点)
- サドル(鞍点)
- スパイラル(渦状点)
今回はノードについて紹介しましょう。
解の挙動は、行列の固有値によって影響を受けます。行列の成分を
\[ \begin{aligned}A= \begin{pmatrix} a&b\\ c&d \end{pmatrix}\end{aligned} \]
と表すとき、その固有方程式は
\[ \begin{aligned} &\det (\lambda I-A) \\&= \lambda^2 -(a+d)\lambda +(ad-bc)\\ &= \lambda^2 -\mathrm{tr}A \lambda +\det A\\&= 0 \end{aligned} \]
となるので、固有値は
\[ \begin{aligned} \lambda = \frac{\mathrm{tr} A \pm \sqrt{(\mathrm{tr} A) ^2 – 4 \det A}}{2} \end{aligned} \]
となります。
ノードとは
2つの固有値がともに実数で、同じ符号であるとき、平衡解はノード(結節点 node)であると呼ばれます。
つまり、\((\mathrm{tr} A) ^2 – 4 \det A\geq 0\)、\(\det A = \lambda_1 \lambda_2 > 0\)のケースです。
ノードは漸近安定または不安定で、解曲線が集中し、それらを結びつけているように見えます。それがおそらくノード(結節点)の由来でしょう。
不安定なノード
\[ \begin{aligned}A= \begin{pmatrix} 1&0\\ 0&2 \end{pmatrix}\end{aligned} \]
のとき、固有値は\(1,2\)で、対応する固有ベクトルは\((1,0),(0,1)\)です。
固有値の実部がともに正のノードは、不安定なノード(unstable node)、湧点(source)と呼ばれます。
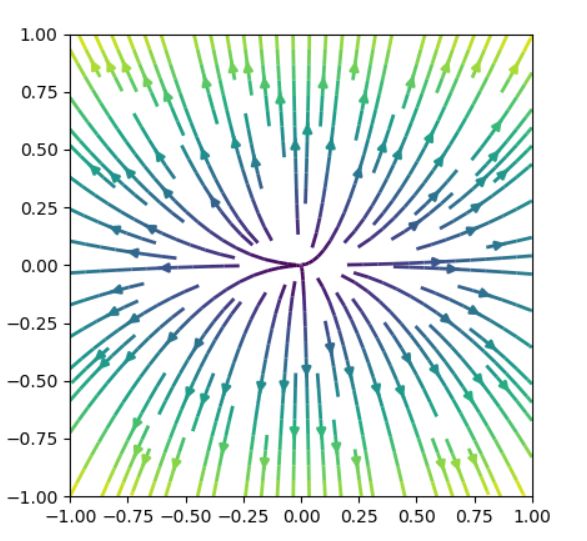
解は一般に\(x(t) =(C_1 e^t,C_2 e^{2t} )\)と表されます。ここから\(t\)を消去すると、\( x_2 = \frac{C_2}{C_1^2 } x_1 ^2\)という曲線が得られますね。
安定なノード
\[ \begin{aligned}A= \begin{pmatrix} -3&0\\0&-1 \end{pmatrix}\end{aligned} \]
固有値は\(-3,-1\)で、対応する固有ベクトルは\((1,0),(0,1)\)です。
固有値の実部がともに負のノードは、(漸近)安定なノード(stable node)、沈点(sink)と呼ばれます。
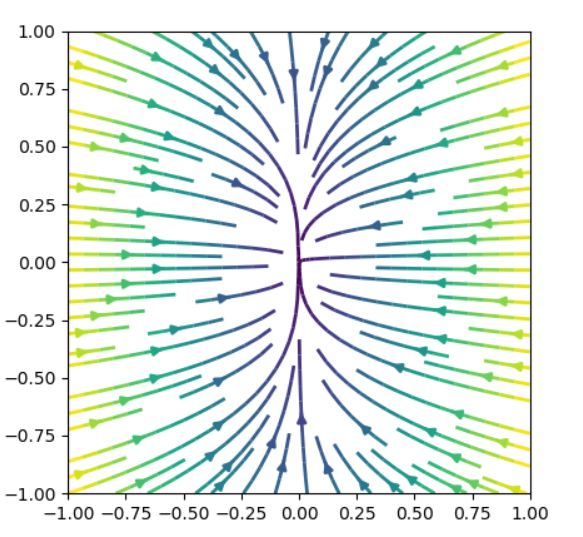
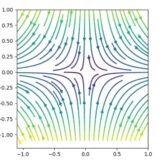
解は一般に\(x(t) = (C_1 e^{-3t},C_2 e^{-t})\)と表されます。\(t\)を消去すると、\(x_2 ^3 = \frac{C_2 ^3}{C_1} x_1\)という曲線が得られます。
スター
\[ \begin{aligned}A= \begin{pmatrix} 2&0\\0&2 \end{pmatrix}\end{aligned} \]
固有値は\(2,2\)で、対応する固有ベクトルは\((1,0),(0,1)\)です。
固有値に重複があり、かつ線形独立な2つの固有ベクトルがあるノードは、スター(星点 star)、真のノード(proper node)と呼ばれます。

解は\(x(t) = (C_1e^{2t}, C_2e^{2t})\)と表されるので、\(t\)を消去すれば\(x_2 =\frac{C_2}{C_1} x_1\)と直線になります。
退化ノード
\[ \begin{aligned}A= \begin{pmatrix} 2&1\\0&2 \end{pmatrix}\end{aligned} \]
固有値は\(2,2\)で、対応する固有ベクトルは\((1,0)\)のみです。
固有値に重複があり、かつ固有空間の次元が1であるノードは、退化ノード(degenerate node)と呼びます。

以上、2次元線形力学系の平衡解の分類として、ノードについて簡単な例を交えて紹介してきました。
基本的には2つの直線(固有ベクトル)があり、安定(もしくは不安定な)平衡点がノードです。実部の符号が同じだと、シンプルでわかりやすいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
なぜ行列式を学ぶのか? 固有値・固有ベクトルの求め方:固有多項式の定義