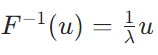どうも、木村(@kimu3_slime)です。
今回は、コンパクトな逆作用素を持つ作用素の固有値の性質を紹介します。
コンパクトな逆作用素を持つ作用素の固有値の性質
ラプラシアン\(A:=-\Delta, A:L^2(\Omega)\to L^2(\Omega)\)は、非有界な作用素であり、そのままでは固有値に関する一般論:ヒルベルト・シュミットの定理は利用できません。
しかし\(A\)はコンパクトな逆作用素\(A^{-1}\)を持つことが知られています。その逆作用素に対してヒルベルト・シュミットの定理を適用することができ、\(A\)の固有値に関する性質が引き出せます。
これはラプラシアンに限らず、コンパクトな逆作用素を作用素全般に使える次のような主張です。
\(H\)を可分なヒルベルト空間とし、その部分空間\(D(G)\)を定義域とする線形作用素\(G:D(G)\to H\)を考えます。さらに、\(G\)は対称で、全射\(R(G)=H\)で、可逆な作用素であり、逆作用素\(G^{-1}\)はコンパクトとします。
このとき、
- 固有値はすべて実数
- 固有値は多くても可算無限個。
- すべての固有値が正であるとき、すべての\(n \in \mathbb{N}\)に対し\(|\lambda_{n+1}| \geq |\lambda_{n}|\)」を満たすように固有値に番号付けするならば、\(\lim_{n \to \infty} \lambda_n =\infty\)
- 固有関数系\((w_n)\)は、\(H\)の完全正規直交系(ヒルベルト基底)となる。
- \(G(u) = \sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle w_n\)と表せる。
となります。
証明
では証明していきましょう。
\(G\)は対称な線形作用素なので、その逆作用素の性質から\(G^{-1}\)も対称な線形作用素です。また\(G^{-1}\)は仮定よりコンパクトで、定義域は全体\(D(G^{-1})=R(G)=H\)なので、次のヒルベルト・シュミットの定理が適用できます。
\(H\)を可分なヒルベルト空間、\(F:H \to H\)をコンパクトで対称な線形作用素とする。
- 固有値はすべて実数
- 固有値は多くても可算無限個。「すべての\(n \in \mathbb{N}\)に対し\(|\lambda_{n+1}| \leq |\lambda_{n}|\)」を満たすように固有値に番号付けするならば、\(\lim_{n \to \infty} \lambda_n =0\)
- 固有関数系\((w_n)\)は、像\(F(H)\)の完全正規直交系(ヒルベルト基底)となる。
- 特に、\(F(u) = \sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle w_n\)と表せる。
- さらに、\(F\)が可逆(単射)ならば、固有関数系は全体\(H\)の完全正規直交系となる。
\(G^{-1}\)の可算個の固有値を\((\mu_n)_n\)、対応する固有関数を\((w_n)_n\)としましょう。これらはすべて実数で、\(|\mu_{n+1}| \leq |\mu_{n}|\)を満たすように並べていて、\(\lim_{n \to \infty} \mu_n =0\)。また、逆作用素が存在し、\(G^{-1}\)は単射であることから、ゼロ固有値は持ちません。
逆作用素と固有値の関係から、\(G^{-1}(w_n)=\mu_n w_n\)と\(G(w_n)= \frac{1}{\mu_n}w_n\)は同値です。そこで、\(\lambda_n = \frac{1}{\mu_n}\)とおきましょう。
\((\lambda_n)_n\)は\(G\)の固有値、\((w_n)\)は\(G\)の固有関数です。\(|\mu_{n+1}| \leq |\mu_{n}|\)は\(|\lambda_{n+1}| \geq |\lambda_{n}|\)に対応します。また、固有値が正であるという仮定のとき、\(\lim_{n \to \infty} \mu_n =0\)は\(\lim_{n \to \infty}\lambda_n =\infty\)に対応します。
また、\(G^{-1}\)は可逆なので(\(G\)がその逆作用素)、固有関数系\((w_n)_n\)は、\(H\)の完全正規直交系となります。
\(u= \sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle w_n\)と展開するならば、\(G\)の線形性と固有値の性質から\(G(u)=\sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle G(w_n)= \sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle w_n\)です。
よって、提示した内容が証明できました。
以上、コンパクトな逆作用素を持つ作用素の固有値の性質を紹介してきました。
作用素はすべてが有界とは限りません。しかし、逆作用素があってコンパクトでありさえすれば、固有値に関する一般論が利用できるのは便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
有界線形作用素、ノルムとは:行列、積分作用素、微分作用素の例
レリッヒ・コンドラショフの定理、コンパクト作用素、コンパクトな埋込みとは