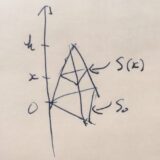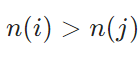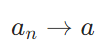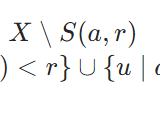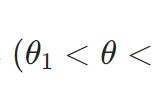
![]() 木村すらいむ
木村すらいむ
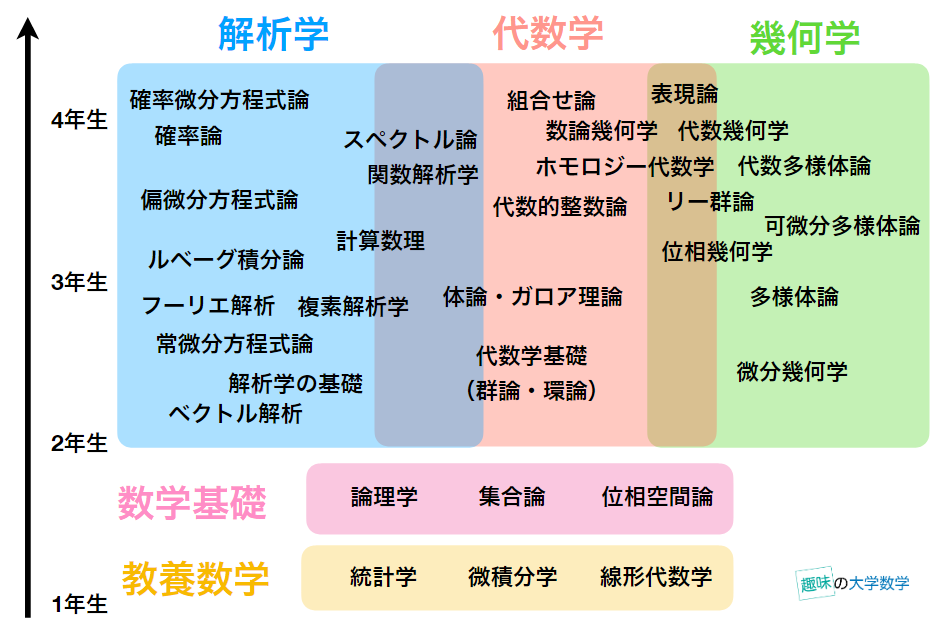
大学で扱われるような高度な数学を、趣味として知りたい人向けの読み物を提供するサイトです。
受験勉強のように、与えられた問題を解くことだけが数学ではありません。
趣味として学びたいという好奇心と「なぜ?」という懐疑心を大切にして、一緒に大学数学の世界に入っていきましょう。
Twitter(@kimu3_slime)でも情報発信してます。
受験勉強のように、与えられた問題を解くことだけが数学ではありません。
趣味として学びたいという好奇心と「なぜ?」という懐疑心を大切にして、一緒に大学数学の世界に入っていきましょう。
Twitter(@kimu3_slime)でも情報発信してます。
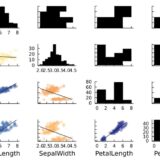
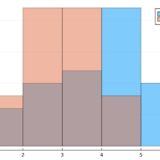
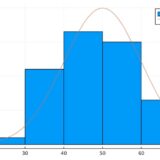
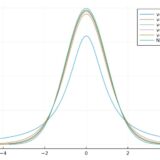
プログラミング・数値計算