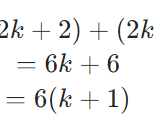連続するn個のaの倍数がnの倍数となる条件、証明

どうも、木村（@kimu3_slime）です。

今回は、連続するn個のaの倍数がnの倍数となる条件とその証明を紹介します。

前提

3つの連続する整数の和は、3の倍数となります。一般に、\(n\)個の連続する整数の和は、\(n\)が奇数のとき、\(n\)の倍数です。

また、連続する3つの偶数の和は、3の倍数（特に、6の倍数）となります。一般に、\(n\)個の連続する偶数の和は、\(n\)の倍数です。

整数は\(1\)の倍数で、偶数は\(2\)の倍数と言えます。より一般に、\(a\)の倍数を考え、その連続する\(n\)個の和が\(n\)の倍数となる条件を考えてみましょう。

連続する\(n\)個の\(a\)の倍数は、\(ak+a,ak+2a,\dots,ak+na\)と表せます。

総和の記号（シグマ記号）を使って和を表し、和の公式\(\sum_{\ell=1}^n \ell = \frac{1}{2}n(n+1)\)によって計算しましょう。

連続する\(n\)個の\(a\)の倍数の和は、

\[(ak+a)+\cdots+(ak+na)\\= \sum_{\ell =1}^{n} (ak+\ell a)\\ = nak+a \cdot \frac{1}{2}n(n+1)\\=n(ak+\frac{a}{2}(n+1))\]

となります。

これが\(n\)の倍数となるのは、\(\frac{a}{2}\)が整数のとき、または\(\frac{1}{2}(n+1)\)が整数となるときです。

つまり、\(a\)が偶数（2の倍数）であるとき、または\(n\)が奇数のとき、連続する\(n\)個の\(a\)の倍数の和が\(n\)の倍数であると言えました。

まとめると、

\(a\)が偶数ならば、\(a\)の倍数の\(n\)個の連続和は常に\(n\)の倍数。
- 特に、\(n\)が奇数のとき、\(2n\)の倍数になる。
\(a\)が奇数であり、かつ\(n\)が奇数のとき、\(a\)の倍数の\(n\)個の連続和は\(n\)の倍数。
- \(a\)が奇数であり、かつ\(n\)が偶数のときは、\(n\)の倍数にはならない。

となりました。