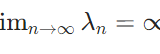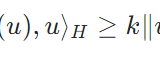どうも、木村(@kimu3_slime)です。
今回は、ラプラシアンが可逆であること、ポアソン方程式が一意な弱解を持つことの証明を紹介します。
導入
ラプラシアンの固有値について調べるためには、それがコンパクトな逆作用素を持つことを示せば良いです。
今回はまず、ラプラシアンが逆作用素を持つことの証明をしましょう。
(有界な領域\(\Omega\)における)ポアソン方程式
\[-\Delta u (x)=f(x) \quad (x \in \Omega) \]
\[ u (x)=0 \quad (x \in \partial\Omega) \]
を弱形式にすると、すべての\(\phi \in H_0 ^1 (\Omega)\)に対し、
\[\int_\Omega \langle \nabla u, \nabla \phi \rangle dx = \int_\Omega f(x)\phi (x)dx \]
を満たすような\(u \in H_0^1 (\Omega)\)を求めよ、という問題になります。
ここで弱形式のラプラシアン\(A=-\Delta\)、\(A:H_0^1(\Omega)\to H^{-1}(\Omega)\)を、\(\phi \in H_0 ^1 (\Omega)\)に対し、
\[\langle A(u),\phi \rangle := a(u,\phi)\]
\[a(u,\phi):=\int_\Omega \langle \nabla u, \nabla \phi \rangle dx \]
と定義できます。\(u \in H_0^1\)を決めると、\(A(u)\)という\(\phi \in H_0^1\)を変数とする有界線形汎関数が決まる、という意味です。
証明
\(A\)が可逆であることを示しましょう。つまり、\(f \in H^{-1}(\Omega)\)に対し、(\(H^{-1}\)、有界線形汎関数としての方程式)\(A(u)=f\)がただひとつの解\(u \in H_0 ^1\)を持つことを示せば良いです。これはポアソン方程式が一意な弱解を持つことの証明にもなります。
有界線形汎関数であること
そのために、\(A(u)\)が\(H_0^1\)上の有界線形汎関数であること(\(A(u) \in H^{-1}\))をまず示しましょう。
\(\alpha\)をスカラー、\(v,w \in H_0^{1}(\Omega)\)とします。微分と積分の線形性、内積の線形性から、
\[\begin{aligned} & \langle A(u),\alpha v+w \rangle\\ &= a(u,\alpha v+w)\\&=\int_\Omega \langle \nabla u, \nabla (\alpha v+w) \rangle dx \\&=\int_\Omega \langle \nabla u, \alpha \nabla v+\nabla w \rangle dx \\&= \int_\Omega \alpha \langle \nabla u, \nabla v \rangle dx+ \int_\Omega \langle \nabla u, \nabla w \rangle dx \\&=\alpha a(u,v)+a(u,w) \\&= \alpha \langle A(u),v \rangle+\langle A(u),w \rangle\end{aligned}\]
となるので、\(A(u)\)は線形作用素(特に実数値なので、線形汎関数)です。
また、\(\Omega\)が有界領域なので、ポアンカレの不等式から導かれる\(H_0^1\)内積に関するコーシー・シュワルツの不等式から、
\[\begin{aligned} &|\langle A(u), \phi \rangle| \\ &= | a(u,\phi)|\\&= |\int_\Omega \langle \nabla u, \nabla \phi \rangle dx | \\&= |\langle u,\phi \rangle_{H_0^1}| \\ &\leq \|u\|_{H_0^1}\|\phi\|_{H_0^1}\end{aligned}\]
となり、\(u\in H_0^1\)であることから、\(\phi\)に依存しない定数\(\|u\|_{H_0^1}\)で評価できています。よって、\(A(u)\)は有界作用素です。
リースの表現定理の適用
ここで関数解析の基本的な定理、リースの表現定理を利用しましょう。
リースの表現定理(Riesz representation theorem)
\(H\)をヒルベルト空間(完備な内積空間)、\(H^{*}\)をその双対空間とする。
どんな有界線形汎関数\(\ell \in H^{*}\)に対しても、次の条件を満たす\(x_\ell \in H\)が一意に存在する。
すべての\(y \in H\)に対し、\(\langle \ell ,y\rangle= \langle x_{\ell},y \rangle_H \)
また、\(\|x_\ell\|_H=\|\ell\|_{H^{*}}\)である。
\(H=H_0^1(\Omega)\)とすると、その双対空間は\(H^{*}=H^{-1}(\Omega)\)です(そもそも\(H^{-1}\)の定義が\(H_0^1\)の双対空間なので)。
よってリースの表現定理から、\(f \in H^{-1}\)に対し、\(\langle f,\phi\rangle =\langle u, \phi\rangle_{H_0^1}\)を満たす\(u \in H_0^1\)が存在します。
ここでさきほどの計算から、\(\langle A(u), \phi \rangle=\langle u, \phi\rangle_{H_0^1}\)でもありました。このような\(u\)は(\(f\)に応じて)一意なので、弱形式のポアソン方程式)\(A(u)=f\)の解\(u\)が一意に存在することが示せました。
これは\(A\)が可逆であることも意味しています。与えられた\(f \in H^{-1}\)に対し、\(A^{-1}(f)=u\)と定めれば、\(A^{-1}:H^{-1}(\Omega)\to H_0^1(\Omega)\)がラプラシアンの逆作用素です。
また、\(\|u\|_{H_0^1}= \|f\|_{H^{-1}}\)となっています。
以上、ラプラシアンが可逆であること、ポアソン方程式が一意な弱解を持つことの証明を紹介してきました。
このラプラシアンが対称な線形作用素で、さらに逆作用素がコンパクトであることを示せば、固有値の性質が引き出せます。これについては別記事にて。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは