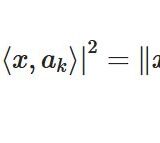コーシー・シュワルツの不等式とは：証明と幾何学的な意味

どうも、木村（@kimu3_slime）です。

今回は、コーシー・シュワルツの不等式の不等式とは何か、その証明と幾何学的な意味を紹介します。

コーシー・シュワルツの不等式とは
シュワルツの不等式の証明と幾何学的な意味
こちらもおすすめ

コーシー・シュワルツの不等式とは

コーシー・シュワルツの不等式（Cauchy–Schwarz inequality）とは、内積とノルムの間に成り立つ次のような不等式です。単にシュワルツの不等式とも。

\(V\)を内積空間とする。任意の\(a, b \in V\)に対し、

\[ \begin{aligned}|\langle a,b \rangle| \leq \|a\| \|b\|\end{aligned} \]

が成り立つ。ただし、ノルムは内積から誘導されるもの \(\|a\| := \sqrt{\langle a,a \rangle}\)。

\(V\)は一般的な内積空間で成り立つもので、さまざまな不等式を生み出します。具体的に書いてみましょう。

\(V= \mathbb{R}^3 \)なら

\[ \begin{aligned}|a_1b_1+a_2b_2+a_3b_3| \leq \sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}\end{aligned} \]

\(V= \mathbb{R}^N \)なら

\[ \begin{aligned}|\sum_{k=1} ^N a_k b_k| \leq \sqrt{\sum_{k=1} ^N a_k^2}\sqrt{\sum_{k=1} ^N b_k^2}\end{aligned} \]

\(V=\ell ^2\)（数列空間）なら

\[ \begin{aligned}|\sum_{k=1} ^\infty a_k b_k| \leq \sqrt{\sum_{k=1} ^\infty a_k^2}\sqrt{\sum_{k=1} ^\infty b_k^2}\end{aligned} \]

\(V=L^2\)（関数空間）なら

\[ \begin{aligned}|\int f(x)g(x)dx| \leq \sqrt{\int f(x)^2 dx }\sqrt{\int g(x)^2 dx }\end{aligned} \]

といった式が成り立ちます。

そもそも、\(\ell ^2 ,L^2\)に内積が定まることを示すために、シュワルツの不等式が必要です。\(\ell ^2 \)の数列、\(L^2\)の関数については、右辺が有限値となるので、内積が有限値として定まることがわかります。

また、ノルムに関する三角不等式\(\|a+b\| \leq\|a\|+\|b\|\)を示すためにも、シュワルツの不等式は使われます。

さらに、一般の線形空間でベクトルの角度を定義するためにも必要です。\(\cos \theta := \frac{\langle a,b\rangle}{\|a\| \|b\|}\)を満たす\(\theta\)が存在してほしい。シュワルツの不等式を使えば、\( -1 \leq \frac{\langle a,b\rangle}{\|a\| \|b\|} \leq 1\)がわかります。

このように、シュワルツの不等式は内積とノルムの間で使える基本的な不等式と言えるでしょう。

シュワルツの不等式の証明と幾何学的な意味

では、シュワルツの不等式\(|\langle a,b \rangle| \leq \|a\| \|b\|\)を証明しましょう。

まず、\(a,b\)のどちらが一方が\(0\)ベクトルのときは、等式が成り立ちます。内積の線形性より

\[ \begin{aligned} \langle a,0\rangle &=\langle a,a-a\rangle \\ &= \langle a,a\rangle-\langle a,a\rangle \\&=0 \ \end{aligned} \]

となるので、\(|\langle a,b \rangle| =0\)。右辺もノルムの性質より、\(\|a\| \|0\| =0\)なので、これらは等しいです。

以降では、\(a \neq 0\)として議論しましょう。そして、\(b\)の\(a\)に対する直交射影を求めるときにできるベクトル\(c\)に注目します（\(a\)の生成する線形空間の直交補空間への\(b\)の射影）。それを考えるためには、\(a,b\)が線形独立であることが必要です。

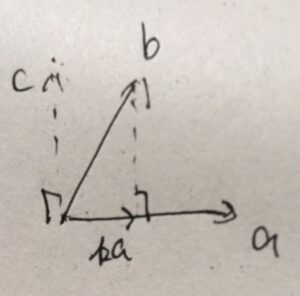
シュワルツの不等式は、この\(c\)の長さ（ノルム）は\(0\)以上ですよ、という主張です。幾何学的には、確かに成り立っていそうな性質です。

\(a\)を定数倍して、\(c\)を求めてみます。直交射影であることから、\(ka+c= b\)、\(\langle a,c\rangle=0\)です。等式において\(a\)との内積を取れば、\(k\langle a,a\rangle +0=\langle a,b\rangle\)なので、\(k= \frac{\langle a,b\rangle}{\langle a,a\rangle }\)と求められます。

\(c= b-\frac{\langle a,b\rangle}{\langle a,a\rangle }a\)です。ノルムの性質から、\(\|c\|\geq 0\)となります。一方、このノルムを展開して整理してみましょう。

\[ \begin{aligned} \|c\|^2 &= \langle b-ka,b-ka\rangle \\ &=\|b\|^2 -2k\langle a,b \rangle +k^2\|a\|^2 \\&= \|b\|^2 -2\frac{\langle a,b \rangle ^2}{\|a\|^2}+\frac{\langle a,b \rangle ^2}{\|a\|^4}\|a\|^2 \\ &= \frac{1}{\|a\|^2}(\|a\|^2\|b\|^2- \langle a,b \rangle ^2)\end{aligned} \]

これが0以上なので、\( \langle a,b \rangle ^2 \leq \|a\|^2\|b\|^2\)です。正の平方根を取れば、\(|\langle a,b \rangle| \leq \|a\| \|b\|\)が得られました。

\(a,b\)が線形従属なケース、\(a=kb\)となるケースを考えましょう。

このとき、\(c= 0\)となるので、さきほどのノルムの展開式から\(\frac{1}{\|a\|^2}(\|a\|^2\|b\|^2- \langle a,b \rangle ^2)=0\)が得られます。\(\|a\|^2\)をかけて正の平方根を取れば、\(|\langle a,b \rangle| = \|a\| \|b\|\)が得られました。

シュワルツの不等式は、直交射影において\(a,b\)の隔たりを表すベクトル\(c\)の大きさが、0以上であることを主張しています。そして、直交射影が考えられないケース、つまり\(a,b\)が線形従属のときは、等号が成り立つと言っているわけですね。

今回はスカラーを実数とする実内積として議論しましたが、複素内積についても同様にしてシュワルツの不等式が成り立つことが示せます。変わるのは途中の内積の展開式の部分だけです。

以上、コーシー・シュワルツの不等式とは何か、その証明と幾何学的な意味を紹介してきました。

抽象的な内積・ノルムの定義・性質から導かれる基本的な不等式ですが、汎用性が非常に高くて便利です。何かの積で表される量を上から評価したいと思ったときは、何かの内積になっていないか見抜き、シュワルツの不等式を使ってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。