ユークリッド空間R^Nの内積、ノルム、距離について解説

どうも、木村（@kimu3_slime）です。

線形代数学で登場するユークリッド空間\(\mathbb{R}^N\)のベクトルは、角度や大きさを測ったりすることができます。

今回は、\(\mathbb{R}^N\)の内積、ノルム、距離とはどういうものか、具体例を交えて紹介していきます。

平面ベクトルの内積、ノルム、距離とは
R^Nの内積、ノルム、距離とは
内積、ノルム、距離の性質
こちらもおすすめ

平面ベクトルの内積、ノルム、距離とは

簡単のため、\(N=2\)、平面\(\mathbb {R}^2\)のベクトルを考えましょう。高校数学のベクトルの復習です。

\(a=(a_1,a_2),b=(b_1,b_2)\)とします。内積は\(\langle a,b\rangle= a_1 b_1+a_2b_2\)、ノルムは\(\|a \| = \sqrt{a_1 ^2+b_1 ^2 }\)、距離は\(d(a,b) = \sqrt{(a_1-b_1)^2 + (a_2 -b_2)^2}\)と定義されるのでした。

高校数学では、内積は\(a\cdot b\)（ドット積）と書いて、ノルムはベクトルの大きさ\(|a|\)と呼ばれていたかもしれません。どちらで言っても同じことです。（内積は外積\(a\times b\)とは別物なので注意）

\(a=(1,0),b=(1,1)\)として計算してみましょう。\(\langle a,b\rangle= =1\)、\(\|a \| = 1, \|b \| =\sqrt{2}\)、\(d(a,b)=1\)となります。

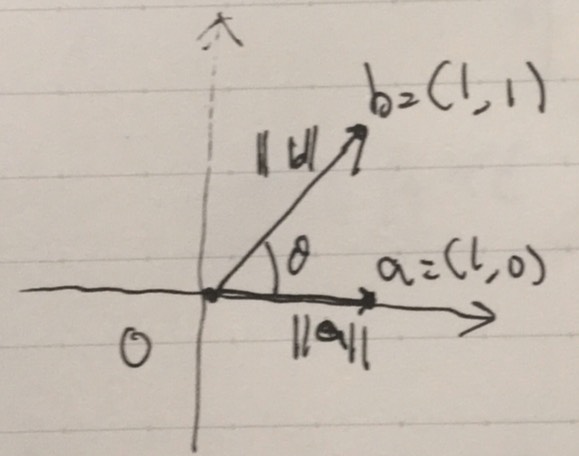
2つのベクトルの距離は、そのまんまベクトルが表す点と点の距離です。1ですね。

ベクトルのノルムは、そのベクトルの長さです。長さは、三角形のピタゴラスの定理に合うように定義されています。\(b\)については、\(1^2+1^2 =(\sqrt{2})^2\)です。

ベクトルの内積は、ベクトルの角度と関連する値です。2つのベクトルのなす角を\(\theta\)とすると、\(\langle a,b\rangle = \|a\| \| b\| \cos \theta\)という関係がありました。今回の例では、\(\cos \theta =\frac{1}{\sqrt {2}}\)です。そのため、なす角（のうち小さい方）は\(\theta = \frac{\pi}{4}\)です。中学数学でも扱う、辺の長さが\(1:1:\sqrt{2}\)で、角度が45度の直角三角形になってますね。

内積は角度に関連していて、2つのベクトルがなす三角形の面積や、行列式とも関係しています。

参考：なぜ行列式を学ぶ？面積・体積との一致、ヤコビアンへの応用

R^Nの内積、ノルム、距離とは

もっと一般の\(N\)次元のベクトルに対しても、内積、ノルム、距離を考えることができます。

\(a=(a_1,a_2,\dots,a_N),b=(b_1,b_2,\dots,b_N)\)としましょう。

\(\langle a,b\rangle= a_1 b_1+a_2b_2+\cdots +a_Nb_N\)

\(\|a \| = \sqrt{a_1 ^2+a_2 ^2+\cdots +a_N ^2 }\)

\(d(a,b) = \sqrt{(a_1-b_1)^2 + (a_2 -b_2)^2 +\cdots +(a_N-b_N)^2}\)

これらはそれぞれ、ユークリッド内積（Euclidean inner product）、ユークリッドノルム（Euclidean norm）、ユークリッド距離（Euclidean distance）と呼ばれます。ユークリッドと言わずに単に内積、ノルム、距離とも。特に言及がなければ、普通はこの定義を用いていることが多いでしょう。

ベクトルのなす角\(\theta\)は、\(\cos \theta = \frac{\langle a,b\rangle}{\|a \|\|b \|}\)により定義されます。内積が0のとき、2つのベクトルは直交している（orthogonal）と呼ばれます。

4次元以上のベクトルなんて、どうイメージしたらいいかわからない、と思いますか？　確かに、平面や空間にそれを図示するのは難しいです。しかし、上で定義した内積、ノルム、距離を使えば、幾何学的な量を掴むことができます。

\(\mathbb{R}^4\)のベクトルは、4つの数の組です。例えば、\(e_1=(1,0,0,0)\)と\(e_4= (0,0,0,1)\)は直交しています。なぜなら、\(\langle e_1,e_4\rangle=0\)なので。その大きさ、ノルムは\(\|e_1\|= \|e_4\|=1\)です（ノルムが1のベクトルを単位ベクトルという）。また、2点の距離は\(d(e_1,e_4)=\sqrt{2}\)と測れます。

2次元空間で、ノルムが1の点の集まり、すなわち原点からの距離が1の点の集まり\(S^1 = \{x \in \mathbb{R}^2 \mid x_1^2 +x_2 ^2 =1\}= \{x \in \mathbb{R} ^2\mid \|x\|=1\}\)は円周です。3次元空間内なら、\(S^2 = \{x \in \mathbb{R}^3 \mid x_1^2 +x_2 ^2 +x_3^ 2 =1\}= \{x \in \mathbb{R} ^3\mid \|x\|=1\}\)は球面です。（考える空間の次元に応じて、考えているノルムが違うことに注意）

そして、\(S^4 = \{x \in \mathbb{R}^4 \mid x_1^2 +x_2 ^2 +x_3^ 2 +x_4 ^2 =1\}= \{x \in \mathbb{R} ^4\mid \|x\|=1\}\)は、超球面と呼ばれます。一般には、\(S^{N-1} = \{x \in \mathbb{R} ^{N-1}\mid \|x\|=1\}\)です。

視覚的にはならないかもしれませんが、内積、ノルム、距離が幾何学的な情報を与えていることがイメージ（？）できてきたでしょうか。

内積、ノルム、距離の性質

線形代数学や数学全般においては、ユークリッド空間の内積、ノルム、距離が持つ性質を抽象化して、（抽象）内積空間、ノルム空間、距離空間というものを考えます。

今回は、ユークリッド内積、ノルム、距離が持つ性質を紹介し、簡単に証明します。

内積の性質（抽象内積の定義）

\(V\)を線形空間とする。2変数関数\(\langle \cdot,\cdot \rangle :V\times V \to \mathbb{R}\)は、次を満たすとき内積と呼ばれる。
任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、
(1) 対称性：\(\langle a,b\rangle =\langle b,a\rangle\)
(2) （二重）線形性：\(\langle \lambda a+c,b\rangle = \lambda \langle a,b\rangle +\langle c,b\rangle\)
(3) 正定値性：\(\langle a,a\rangle \geq 0\)。\(a\neq 0\)ならば\(\langle a,a\rangle > 0\)。
内積をもつ線形空間を、内積空間、計量線形空間と呼ぶ。
（これは実内積の定義。複素内積を考えるときは、少し定義が変わる。）

ユークリッド内積がこれらの性質を満たすことを確かめます。

(1) 実数の積は可換なので、\(\langle a,b\rangle =a_1b_1+\cdots + a_N b_N = b_1 a_1 +\cdots b_N a_N =\langle b,a\rangle\)です。

(2) 実数の分配法則を使って計算すると、次の式が成り立つのがわかります。

\[ \begin{aligned} \langle \lambda a+c,b\rangle&= (\lambda a_1 +c_1)b_1 +\cdots + (\lambda a_N +c_N)b_N \\&= \lambda( a_1 b_1 +\cdots + a_N b_N)+(c_1b_1 +\cdots +c_N b_N) \\&= \lambda \langle a,b\rangle +\langle c,b\rangle \end{aligned}\]

(3) 任意の実数\(x\in \mathbb{R}\)に対し、\(x^2 \geq 0\)です。\(x \neq 0 \)ならば、\(x^2 >0\)です。したがって、\(\langle a,a\rangle = a_1^2 +\cdots +a_N ^2 \geq 0\)。\(a\neq 0\)ならば、\(a_i \neq 0\)となる\(i\)が存在するので、\(\langle a,a\rangle = a_1^2 +\cdots +a_N ^2 \geq a_i ^2> 0\)です。

ノルムの性質（抽象ノルムの定義）

\(V\)を線形空間とする。1変数関数\(\| \cdot \| :V \to \mathbb{R}\)は、次を満たすときノルムと呼ばれる。
任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、
(1) 正定値性：\(\|a\| \geq 0\)。\(a= 0\)は\(\|a\| = 0\)と同値である。
(2) 斉次性：\(\|\lambda a\| = |\lambda| \| a\| \)
(3) 三角不等式（劣加法性）：\(\|a+b\| \leq \|a\|+ \|b\|\)
ノルムを持つ線形空間を、ノルム空間と呼ぶ。

これも証明していきましょう。

まず、\(\|a\| =\sqrt {a_1^2+\cdots +a_N^2}= \sqrt{\langle a,a\rangle}\)が成り立っています。

(1) 内積の正値性より\( \sqrt{\langle a,a\rangle} \geq 0\)なので、\(\|a\| \geq 0\)です。また、\(a= 0\) であるとき、\(\|a\| =\sqrt{\langle 0,0\rangle} =0\)です。逆に\(\|a\| = 0\)とすると、\({\langle a,a\rangle} =0 \)なので、内積の性質(3)の対偶より\(a=0\)です。

(2) 内積の線形性より、次のように計算できます。

\[ \begin{aligned} \|\lambda a\|&= \sqrt{\langle \lambda a, \lambda a\rangle} \\&= \sqrt{ \lambda ^2 \langle a, a\rangle} \\&= |\lambda| \| a\| \end{aligned} \]

(3) 内積の線形性より、\(\|a+b\| ^2= \langle a+b,a+b\rangle = \langle a,a\rangle+ 2\langle a,b\rangle+\langle b,b\rangle \)です。ここで（コーシー-）シュワルツの不等式\(|\langle a,b\rangle | \leq \|a\| \|b\|\)を認めて進みます（高校数学レベルで証明できます）。シュワルツの不等式より、\( \langle a,a\rangle+ 2\langle a,b\rangle+\langle b,b\rangle \leq \|a\|^2 +2\|a\| \|b\| +\|b\|^2 =(\|a\|+\|b\|)^2 \)です。\(\|a+b\|\geq 0 ,\|a\|+\|b\| \geq 0\)なので、\(\|a+b\| \leq \|a\|+ \|b\|\)が得られました。

距離の性質（抽象距離の定義）

\(V\)を集合とする。2変数関数\(d :V\times V \to \mathbb{R}\)は、次を満たすとき距離と呼ばれる。
任意の\(a,b,c\in V\)に対し、
(1) 正定値性：\(d(a,b)\geq 0\)。\(a=b\)は\(d(a,b)=0\)と同値である。
(2) 対称性：\(d(a,b)=d(b,a)\)
(3) 三角不等式：\(d(a,b) \leq d(a,c)+d(c,a)\)
距離を持つ集合を、距離空間と呼ぶ。

最後に、これも証明しましょう。

まず、\(d(a,b)= \sqrt {(a_1-b_1)^2+\cdots +(a_N- b_N)^2 }= \|a-b\|\)が成り立っています。

(1) ノルムの非負性より、\(d(a,b)= \|a-b\|\geq 0 \)です。また、\(a=b\)は\(a-b=0\)と同値なので、ノルムの正定値性より\(\| a-b\|=0\)、すなわち\(d(a,b)=0\)と同値です。

(2) ノルムの斉次性より、\(d(a,b)=\| -(b-a)\| = |-1| \|b-a\| =d(b,a)\)が成り立ちます。

(3) ノルムの三角不等式より、\(d(a,b)= \| (a-c)+(c-b)\| \leq \|a-c\|+\|c-b\|=d(a,c)+d(c,a) \)です。

以上のことをまとめると、ユークリッド空間\(\mathbb{R}^N\)には、内積、ノルム、距離が定まっています。つまり、ユークリッド空間は、内積空間であり、ノルム空間であり、距離空間でもあるわけです。

今回の証明を見ればわかるように、（抽象）内積があればノルムを定義でき、ノルムがあれば距離を定義できます。ユークリッド空間に限らず、内積空間はノルム空間であり、ノルム空間は距離空間として見ることができます。逆の見方、距離から内積を定めるような方法は一般にありません。このあたりの話は、位相空間論や関数解析で学ぶでしょう。