どうも、木村(@kimu3_slime)です。
線形代数学を学んでいて、(抽象)ベクトル空間が出てきて戸惑った経験はあるでしょうか。
その具体例には様々ありますが、基本的なものは\(N\)次元の数ベクトル空間・ユークリッド空間\(\mathbb{R}^N\)です。
今回は、ベクトルの理解に必要な順序対と直積集合、\(\mathbb{R}^N\)が抽象ベクトル空間の定義を満たすことを紹介しようと思います。
ベクトルと順序対、直積集合
線形代数学の教科書で、次のような記述を目にして困惑した覚えがあります。
集合\(V\)が次の条件を満たすとき、\(V\)をベクトル空間という。ベクトル空間の要素をベクトルという。
(条件略)
\(N\)を1以上の自然数とする。
\(\mathbb{R}^N:=\{(x_1,\dots,x_N)\mid x_1,\dots,x_N \in \mathbb{R} \} \) を\(N\)次元数ベクトル空間という。これはベクトル空間の具体例である。
今になって思えば、ここで具体例として挙げられていた\(\mathbb{R}^N:=\{(x_1,\dots,x_N)\mid x_1,\dots,x_N \in \mathbb{R} \} \) が何なのかよくわかっていなかったんですね。
まず前提として、初歩的な集合論の知識が求められています。
例えば、右辺を一般的に書けば、\(\{x \mid P(x)\}\)となります。これは条件\(P(x)\)を満たす\(x\)の集合という意味で、内包的記法と呼ばれるものです。
\(\{(x_1,\dots,x_N)\mid x_1,\dots,x_N \in \mathbb{R} \}\\= \{ y \mid (\exists x_1,\dots,x_N \in \mathbb{R})(y=(x_1,\dots,x_N)) \}\)と、少し書き方が違う部分は読み替えられます。\(N\)個の実数\(x_1,\dots, x_N\)によって、\(y=(x_1,\dots,x_N)\)と表される\(y\)の集合です。
そして\(\mathbb{R}\)は、実数全体(real numbers)の集合を表します。
参考:集合論入門:集合の定義、数の集合、ラッセルのパラドックス、述語論理、量子化とは:全称記号(∀)と存在記号(∃)、数学における例と否定
では、\((x_1,\dots,x_N)\)とは何なのでしょうか。結論から言えば、それは順序対(じゅんじょつい)です。
\(N=2\)のときでイメージしましょう。平面のベクトルは、2つの数の組によって\((1,2)\)といったように表されます。ただし、同じ1と2で表されると言っても、\((1,2) \neq (2,1)\)です。これがなぜ不等号なのかといえば、前者の第1成分は1、後者の第1成分は2となっていて、同じ成分の値が異なっているからです。順番が違えば別物と考えます。
順序対(ordered pair)とは、いくつかの要素を順序を考慮して組にしたもののことです。\(N\)-組(\(N\)-tuple)とも。
2つの順序対が等しい\((x_1,x_2)=(y_1,y_2)\)ことを、すべての成分が等しい\(x_1=y_1,y_1=y_2\)によって定義します。
一般化すれば、\((x_1,\dots,x_N)= (y_1,\dots,y_N)\)とは、すべての成分\(x_1=y_1,\dots,x_N=y_N\)が等しいこと。この否定\((x_1,\dots,x_N)\neq (y_1,\dots,y_N)\)は、ある成分\(k\)で\(x_k \neq y_k\)なるものが存在すること、と言えますね。
(公理的集合論では、順序対を集合として定義できます。参考:公理的集合論をわかりやすく解説:ZFC公理系を例に)
ここまで来れば、\(\mathbb{R}^2=\{(x_1,x_2)\mid x_1,x_2 \in \mathbb{R} \} \) や\(\mathbb{R}^N:=\{(x_1,\dots,x_N)\mid x_1,\dots,x_N \in \mathbb{R} \} \) の意味はわかったでしょうか。
\(N\)次元のベクトルの集合は、およそ順序対の集まりのことです。(本当はベクトルと呼ばれるためには順序対同士の計算規則、和とスカラー倍が定まっている必要がありますが)
こうした順序対の集まりは、集合論においては一般に直積集合(ちょくせきしゅうごう)と呼ばれます。
集合\(A,B\)の直積集合(product set)\(A\times B\)は、
\[ \begin{aligned}A\times B := \{(a,b) \mid a\in A, b \in B \}\end{aligned} \]
と定義されます。デカルト積(Cartesian product)とも。
\(A=B=\mathbb{R}\)の場合を考えれば、\(\mathbb{R}^2 = \mathbb{R}\times \mathbb{R}\)です。右上の数は、直積している集合の数を表すものということ。
直積集合の直積集合を考えていけば、\(N\)個の直積が考えられます。こうして得られるのが\(\mathbb{R}^N = \mathbb{R}\times \cdots \times \mathbb{R}\)です。
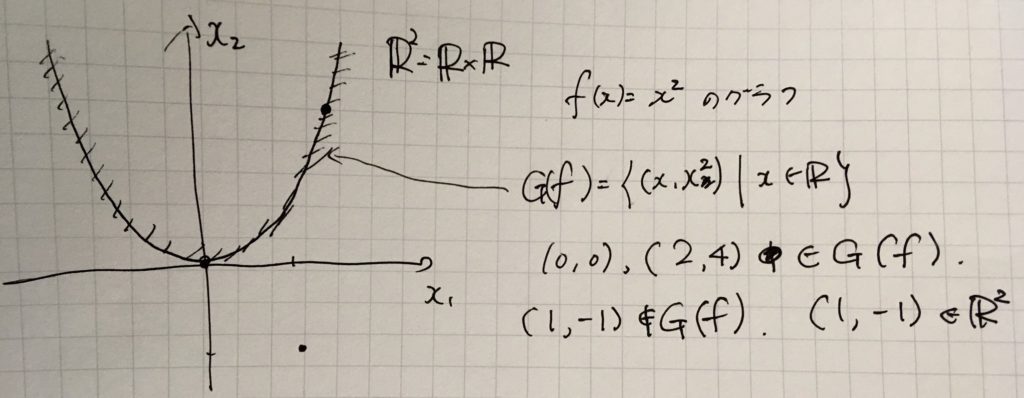
例えば、1変数実数値関数\(f:\mathbb{R}\to \mathbb{R}\)のグラフは、直積集合\(\mathbb{R}^2\)の部分集合として認識できます。
\[ \begin{aligned}G(f):=\{(x_1,x_2) \mid x_1 \in \mathbb{R}, x_2=f(x_1)\}\end{aligned} \]
R^Nと抽象ベクトル空間の定義
こうして定義した\(\mathbb{R}^N \)に、次のような計算規則を導入しましょう。
\(x=(x_1,\dots,x_N),y=(y_1,\dots,y_N)\in \mathbb{R}^N\)、\(a\in \mathbb{R}\)に対し
\[ \begin{aligned}x+y=(x_1+y_1,\dots, x_N+ y_N)\end{aligned} \]
\[ \begin{aligned}ax:= (ax_1,\dots,a x_N)\end{aligned} \]
です。この計算結果もまたサイズが同じ順序対で、\(x+y ,ax \in \mathbb{R}^N\)。これをベクトルの和、スカラー乗法と呼びます。両者は合わせて、線形演算と呼ばれます。
(なぜ単に積と呼ばずにスカラー乗法と呼ぶかと言えば、内積や外積と呼ばれる積の概念が他にあるからです)
こうして定義した\(\mathbb{R}^N\)が、抽象ベクトル空間の定義を満たすことを確かめてみましょう。
抽象ベクトル空間・線形空間(vector space, linear space)とは、次の条件を満たす集合\(V\)です。
\(V\)の任意の要素\(x,y,z\)、任意の数\(a,b\in \mathbb{R}\)に対し、和\(x+y \)、スカラー乗法\(ax \)と呼ばれる\(V\)の要素が定まり、次の条件を満たす。
結合法則:\((x+y)+z = x+(y+z)\)
交換法則:\(x+y =y+x\)
ゼロベクトルの存在:\(\exists o(o+x =x)\)
逆ベクトルの存在:\(\exists w (x+w=o)\)。これを逆ベクトルと言い、\(w=-x\)と書く。
分配法則:\((a+b)x= ax+bx\)
分配法則:\(a(x+y)=ax+ ay\)
両立条件:\((ab)x= a(bx)\)
スカラー乗法の単位要素:\(1x =x\)
順に確かめていきましょう。順序対のカッコと計算の優先順位を表すカッコを混同しないように注意。
\((x+y)+z=(x_1+y_1,\dots,x_N+y_N)+z\\=(x_1+y_1+z_1,\dots,x_N+y_N+z_N)\)
\(x+(y+z)=x+(y_1+z_1,\dots,y_N+z_N)\\=(x_1+y_1+z_1,\dots,x_N+y_N+z_N)\)
なので、結合法則は成り立ちます。
\(x+y=(x_1+y_1,\dots, x_N+y_N)\\ =(y_1+x_1,\dots,y_N+x_N)=y+x\)
なので、交換法則は成り立ちます。
\(o:=(0,\dots,0)\)と定めれば、\(o+x=(0+x_1,\dots,0+x_N)\\ =(x_1,\dots,x_N)=x\)で、ゼロベクトルは存在します。
\(x\)に対して\(w=(-x_1,\dots,-x_N)\)と定めれば、\(x+w=(x_1+(-x_1),\dots,x_N+(-x_N))\\=(0,\dots,0)=o\)が成り立ち、逆ベクトルは存在します。
\((a+b)x =((a+b)x_1,\dots,(a+b)x_N)\\ =(ax_1+bx_1,\dots,ax_N+bx_N)=(ax_1,\dots,ax_N)+\cdots+(bx_1,\dots,bx_N) \\=a(x_1,\dots,x_N)+b(x_1,\dots,x_N) =ax+bx\)
\(a(x+y)=(a(x_1+y_1),\dots,a(x_N+y_N)) \\=(ax_1+ay_1,\dots,ax_N+ay_N)=(ax_1,\dots,ax_N)+(ay_1,\dots,ay_N)\\=a(x_1,\dots,x_N)+a(y_1,\dots,y_N)=ax+ ay\)
なので、分配法則は成り立ちます。
\((ab)x=((ab)x_1,\dots,(ab)x_N)\\=(a(bx_1),\dots,a(bx_N))=a(bx_1,\dots,bx_N)= a(bx)\)
で、両立条件は成り立ちます。
\(1x=(1\cdot x_1,\dots,1\cdot x_N) =(x_1,\dots,x_N)=x\)
なので、スカラー乗法の単位要素が機能しています。
以上によって、\(\mathbb{R}^N\)が抽象ベクトル空間の定義を満たすことが確かめられました。
そもそも、抽象ベクトル空間の定義は、\(\mathbb{R}^N\)が持つ順序対のベクトル演算の性質を取り出して、\(\mathbb{R}^N\)に限らないの一般の集合\(V\)に当てはめられるように抽象化したもの、と言えるでしょう。
行列全体、1変数多項式全体、実数列全体、1次方程式の解全体、連続関数全体のなす集合は、抽象ベクトル空間であることが知られています。
今回の抽象ベクトル空間の定義では、スカラー乗法が\(\mathbb{R}\)を使ったもので、実ベクトル空間・実線形空間と呼ばれます。
この係数を複素数\(\mathbb{C}\)にしても議論は同様で、その場合は複素ベクトル空間・複素線形空間と呼ばれます。複素数全体\(\mathbb{C}\)や、その直積である\(N\)次元の複素数全体\(\mathbb{C}^N\)は、複素線形空間です。(適切な定義を与え、確かめてみてください)
今回は、\(N\)次元の数ベクトル空間・ユークリッド空間\(\mathbb{R}^N\)は何の集合なのか、ベクトルは順序対の一種であり、順序対の集合は一般に直積集合と呼ばれることを紹介しました。その上で、直積集合にベクトル演算を導入すると、抽象ベクトル空間の定義を満たすことを確かめました。
初めて線形代数学を学び、行列論から線形空間論に入ってつまづく人は少なくないのではないでしょうか。今回紹介した、順序対や直積集合の考え方にまで立ち返ると、理解が進むはずです。
木村すらいむ(@kimu3_slime)でした。ではでは。
日本評論社 (2008-12-10T00:00:00.000Z)
¥1,430
東京大学出版会 (1966-03-31T00:00:01Z)
¥2,090
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
述語論理、量子化とは:全称記号(∀)と存在記号(∃)、数学における例と否定