どうも、木村(@kimu3_slime)です。
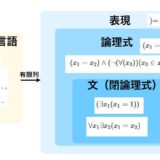
前回、公理的集合論を記述するための言語、論理式、文について解説しました。(集合論の公理だけいきなり見てもわからないと思うので、まずはこちらからどうぞ。)
今回はそれを使った公理的集合論の入門として、特にZFC公理系を紹介したいと思います。
ZFC公理系とは
ZFC公理系(ZFC axioms)とは、集合とはどのようなものであるかを定める、次のような文(sentence)の集まりです。
ZFCという名前は、エルンスト・ツェルメロ(Ernst Zermelo)とアドルフ・フレンケル(Adolf Fraenkel)、そして選択公理(axiom of choice)から取られました。
集合の存在公理(set existence):\[ \begin{aligned}\exists x (x=x)\end{aligned} \]
外延性の公理(exntensionality):\[ \begin{aligned}\forall x\, \forall y \,(\forall z \,(z\in x \Leftrightarrow z \in y)\Rightarrow x=y)\end{aligned} \]
内包性の公理(comprehension scheme)、分出の公理(separation scheme):\(\phi\)を\(x,z,w_1,\dots,w_n\)を自由変数にもつ論理式として、\[ \begin{aligned}\forall z\,\forall w_1,\dots,w_n\,\exists y \, \forall x \,(x\in y \,\Leftrightarrow \, (x\in z) \land \phi)\end{aligned} \]
和集合の公理(union):\[ \begin{aligned}\forall \mathcal{F} \, \exists A\,\forall x ( \exists Y (x\in Y \land Y \in \mathcal{F}) \Leftrightarrow x \in A)\end{aligned} \]
対の公理(pairing):\[ \begin{aligned}\forall x\, \forall y \, \exists z \, (x\in z \land x \in z)\end{aligned} \]
置換の公理(replacement scheme):\(\phi\)を\(x,y,A,w_1,\dots,w_n\)を自由変数にもつ論理式として、\[\begin{aligned}\forall A\, \forall w_1,\dots,w_n\, [(\forall x \in A \, \exists!y\, \phi )\Rightarrow \\(\exists Y\,\forall x \in A \,\exists y \in Y \, \phi)] \end{aligned} \]
無限の公理(infinity):\[ \begin{aligned}\exists x\, ( \emptyset \in x \land \forall y\in x(S(y)\in x))\end{aligned} \]
冪集合の公理(power set):\[ \begin{aligned}\forall x \,\exists y \,\forall z(z \subset x \Rightarrow z \in y)\end{aligned} \]
基礎の公理(foundation)、正則性の公理(regularity):\[ \begin{aligned}\forall x [\exists a \in x \Rightarrow \exists y(y \in x \land \lnot \exists z(z \in x \land z \in y))]\end{aligned} \]
選択公理(choice):\[ \begin{aligned}\forall A\, \exists R\, (R \text{は} A \text{を整列する})\end{aligned} \]
(無限の公理、冪集合の公理、選択公理だけ新たな記号が登場しており、文ではないように見えますが、文です。後で説明します)
公理系は長いように見えますが、集合論の初歩に馴染んだ人ならば、普通の集合の性質を詳しく述べていることに、後に納得できるかと思います。
ZFCの公理をひとつひとつ順に見て、その意味を解説していきましょう。
集合の存在公理
集合の存在公理(set existence):\[ \begin{aligned}\exists x (x=x)\end{aligned} \]
文字通り、集合と呼ばれうる対象が存在することを述べた公理です。
また、\(= ,\in \)という記号について
\[ \begin{aligned}\forall x\, \forall y \,( x=y )\Rightarrow \forall z(z\in x \Leftrightarrow z \in y)\end{aligned} \]
も、明示的に述べられることはなくとも、公理とされています。
もし2つの集合\(x,y\)が「等しい」ならば、そのすべての要素\(z\)は\(x\)に属することと\(y\)に属することは同値、というわけですね。当然成り立っていてほしい性質です。逆に、集合2つが等しいのに、一方の集合にしか属さない要素があったら困ります。
集合の存在公理は、他の公理(無限公理)から導けるので、ZFC公理系に含めないこともあります。が、ここでは議論がわかりやすいので、述べておいて良いでしょう。
外延性の公理
外延性の公理(exntensionality):\[ \begin{aligned}\forall x\, \forall y \,(\forall z \,(z\in x \Leftrightarrow z \in y)\Rightarrow x=y)\end{aligned} \]
これはどのような集合についても、同じ要素が属しているならば、同じ集合であると考えると言っています。
さきほど、その逆も成立していることを確認しました。これらを合わせると、集合のが等しいことの定義です。
\[ \begin{aligned}A=B :\Leftrightarrow \forall x( x\in A \Leftrightarrow x \in B)\end{aligned} \]
つまり、集合とは要素の集まりですが、それは\(\{1,1,2\}=\{1,2\}\)というように、重複のない要素の集まりによって決まった対象であるわけです。同じ要素を持つ集合は一意である、とも言いかえられますね。
外延性の公理は、集合\(A,B\)が等しい\(A=B\)とことの定義を、明確に定めています。
内包性の公理・分出の公理
内包性の公理(comprehension scheme)、分出の公理(separation scheme):\(\phi\)を\(x,z,w_1,\dots,w_n\)を自由変数にもつ論理式として、\[ \begin{aligned}\forall z\, \forall w_1,\dots,w_n\,\exists y \, \forall x \,(x\in y \, \Leftrightarrow \, (x\in z) \land \phi)\end{aligned} \]
これは集合\(z\)のうち論理式\(\phi \)を満たすものを集めた集合、内包記号による集合\(y\)が存在することを述べています。この\(y\)を
\[ \begin{aligned}\{x \mid x \in z \land \phi(x)\}=:\{ x \in z \mid \phi (x)\} \end{aligned} \]
と書くわけですね。\(\forall z\)はベースとなる集合をどう設定しても良いし、\(\forall w_1,\dots,w_n\)は\(\phi\)が\(x\)以外の変数を持っていても良いと述べています。
特に、\(A:=z\)、\(\phi(x) :\Leftrightarrow x \not \in B\)とすれば、集合\(A\)から\(B\)を引いた差(set difference)
\[ \begin{aligned}A \setminus B :=\{ x \in A \mid x \not \in B\} \end{aligned} \]
が定義できます。特に\(A\subset B\)のとき(部分集合の定義は後ほど)、\(A\setminus B\)を\(A\)の(\(B\)に対する)補集合(complement)と言います。
内包性の公理によって、ラッセルのパラドックスは排除、というか集合として定義していないことになります。仮に\(\phi\)が\(y\)に依存してよく、
\[ \begin{aligned}\exists y \, \forall x \,(x\in y \, \Leftrightarrow \, (x\in z) \land (x \notin y))\end{aligned} \]
という\(y\)が存在したとしましょう。すると、すべての\(x\)に対して\(x\not \in z\)が成立します。つまり、すべての集合\(z\)は要素を持たない(空集合)となってしまいます。虚しいですね。内包性の公理では、論理式\(\phi\)における変数\(y\)は自由ではなく束縛されているので、このケースは起こりません。(さらに、内包性公理から、すべての集合を含むような集合は存在しないことが言えます。)
内包性公理は、
\[ \begin{aligned}\exists y \, \forall x \,(x\in y \, \Leftrightarrow \, \phi)\end{aligned} \]
ではありません。この形だと、ラッセルのパラドックスの対象が集合となり、矛盾を起こします。あくまで、集合\(z\)に対してそれに条件\(\phi\)を付け加えたものが集合となることを、内包性公理は主張します。論理式そのものだけではなく、先立つ集合が必要となることに注意しましょう。
また、内包性公理によって、空集合(empty set)の存在が言えます。つまり、集合の存在定理より存在する集合\(z\)に対して
\[ \begin{aligned}\emptyset := \{ x \in z \mid x \not= x\}=\{ x \in z \mid (x\in x) \land (x \not \in x)\}\end{aligned} \]
が存在します。外延性公理より、空集合は\(z\)によらず一意に定まります。ファイ\(\phi\)と空集合\(\emptyset\)は似ていますが、別物なので注意。
空集合には、何の要素も属していません。なぜなら、\(x \in \emptyset\)を満たす\(x\)が存在したとすると、\(x \neq x\)という矛盾を導くからです。つまり、\(\forall x (x \not \in \emptyset)\)が成立します。
ここで\(\subset\)という記号を、
\[ \begin{aligned} A \subset B :\Leftrightarrow \forall x ( x\in A \Rightarrow x \in B)\end{aligned} \]
と定義します。このとき、\(A\)は\(B\)の部分集合(subset)である\( A \subset B\)というのでした。
任意の集合\(A\)に対して、\(A \subset A\)、\(\emptyset \subset A\)が成立していますね。
今までは集合\(x\)が存在すると言ってもそれがどんなものかわかりませんでしたが、少なくとも空集合は存在することがわかりました。これを使って、多くの集合を生み出していくことができます。
和集合の公理
和集合の公理(union):\[ \begin{aligned}\forall \mathcal{F} \, \exists A\,\forall x ( \exists Y (x\in Y \land Y \in \mathcal{F}) \Leftrightarrow x \in A)\end{aligned} \]
例えば、\(\mathcal{F}=\{\{1\},\{1,2\},\{2,3\}\}\)をイメージしてみてください。この公理から、\(\mathcal{F}\)は任意の集合の集まり(集合族)を想定し、その和集合\(A=\bigcup \mathcal{F}\)が存在することが導けます。
つまり、\(\mathcal{F}\)に対して、
\[ \begin{aligned}\bigcup \mathcal{F} := \{x \in A \mid \exists Y \in \mathcal{F } (x \in Y) \} \end{aligned} \]
という集合が存在します。これを集合族\(\mathcal{F}\)の和集合(union)と呼びます。\(\bigcup \mathcal{F} = \bigcup _{Y\in \mathcal{F}} Y\)とも書かれますね。
一方で、\(\mathcal{F} \neq \emptyset, B\in \mathcal{F}\)のとき、集合族\(\mathcal{F}\)の共通部分(intersection)
\[ \begin{aligned}\bigcap \mathcal{F} := \{x \in B \mid \forall Y \in \mathcal{F } (x \in Y) \} \end{aligned} \]
の存在が言えます。こちらは内包性の公理によるもので、和集合の公理は必要ありませんし、独自の「共通部分の公理」も必要ないわけです)。(もし\(\mathcal{F} =\emptyset\)のときは、共通部分は集合全体の集合となり、定義されません。)
ここで述べた和集合、共通部分は、任意の\(\mathcal{F} \)に対するものです。つまり、有限集合族に限らず、無限(可算・非可算)集合族に対しても、和集合と共通部分が必ず存在している、と言えます。
参考:無限集合の多さ(濃度)はどのくらい? 可算無限、カントールの対角線論法とは
対の公理
対の公理(pairing):\[ \begin{aligned}\forall x\, \forall y \, \exists z \, (x\in z \land x \in z)\end{aligned} \]
これによって、2つの集合\(x,y\)を組み合わせた対(pair)と呼ばれる集合の存在が言えます。つまり、
\[ \begin{aligned}\{x,y\} := \{ v \in z \mid v = x \lor v = y\}\end{aligned} \]
です。このような集合は、\(x,y\)のみにより決まり、外延性の公理から一意です。対の特殊なケースとして、一元集合(singleton)\(\{ x\}:= \{ x,x\}\) が定義されます。
さらに対を使って、その順序に意味があるような対、順序対(orderd pair)が定義できます。
\[ \begin{aligned}(x,y):= \{\{x\},\{x,y\}\} \end{aligned} \]
もし\((x,y)=(z,w)\)なら、\(x=z \land y=w\)が成り立ちます(その逆も)。
さらに、\((a,b,c):= ((a,b),c)\)としていくことで、一般に\(n\)-組(n-tuple)が定義できますね。
順序対は、直積集合、例えば高次元のユークリッド空間\(\mathbb{R}^N\)の定義に使われます。僕が集合論を学び始めた当時、この順序対に関する約束をはっきりと認識していなくて、理解が進まなかったような記憶があります。
参考:集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
対の公理と和集合の公理を合わせて、2つの集合\(A,B\)の和集合、共通部分を、\(\mathcal{F} =\{A,B\}\)のときとして定義できます。
\[ \begin{aligned}A\cup B := \bigcup \{A,B\},\quad A\cap B:= \bigcap \{A,B\}\end{aligned} \]
こうすれば、有限集合を
\[ \begin{aligned} \{1,3,5\} = \{1\} \cup \{3,5\}\end{aligned} \]
といったように表記する書き方(外延的記法)が正当化されますね。
置換の公理
置換の公理(replacement scheme):\(\phi\)を\(x,y,A,w_1,\dots,w_n\)を自由変数にもつ論理式として、\[\begin{aligned}\forall A\, \forall w_1,\dots,w_n\, [(\forall x \in A \, \exists!y\, \phi )\Rightarrow \\(\exists Y\,\forall x \in A \,\exists y \in Y \, \phi)] \end{aligned} \]
(\(\exists !\)は一意に存在することを意味します)
これを使うと、\(A,B\)の直積集合(cartesian product)
\[ \begin{aligned}A \times B = \{(x,y) \mid x \in A \land y \in B\}\end{aligned} \]
が集合として存在することを示せます(詳細は長いので簡単に)。(\(n\)個の直積もここから作れます)
ある固定した\(y \in B\)に対し、\((A,y)\)の組のようなものが対の公理、置換の公理から作れます。
\[ \begin{aligned}\mathrm{prod }(A,y):= \{ z \mid \exists x \in A (z= (x,y))\}\end{aligned} \]
置換の公理は、もし\(x\)に応じてある条件\(\phi\)を満たす\(y\)が一意に存在するならば、そのような条件\(\phi\)を満たす\(x,y\)の組の集合が存在する、と言っていますね。「対応関係」を集合に置き換える公理です。
さらに同様のことをして、\((A,B)\)の組のようなものが作れ、その和集合として直積が定義されます。
さらには、関係(relation)が定義できます。
それは、順序対の集合です。つまり、直積集合\(A\times B\)の部分集合\(R\)を、二項関係(binary relation)と呼びます。もし\((x,y)\in R\)なら、\(x,y\)は関係していると考えるわけですね(直積が\(n\)個なら\(n\)項関係です。)
そして関係を使えば、写像・関数(mapping, function)が定義できます。
関係\(R\)に対して一般に、定義域(domain)、値域(range)
\[ \begin{aligned}\mathrm{dom}(R):= \{ x \mid \exists y( (x,y) \in R)\}\end{aligned} \]
\[ \begin{aligned}\mathrm{ran}(R):= \{ y \mid \exists x( (x,y) \in R)\}\end{aligned} \]
が(内包性公理より)定義できます。そして関係\(f\)が写像であるとは、
\[ \begin{aligned}\forall x \in \mathrm{dom}(f)\, \exists ! y \in \mathrm{ran}(f) ((x,y) \in f)\end{aligned} \]
を満たすような関係ですね。定義域の任意の要素に対し、値域の要素が一意に定まる、そういう関係を写像と呼ぶわけです。
無限の公理
無限の公理(infinity):\[ \begin{aligned}\exists x\, ( \emptyset \in x \land \forall y\in x(S(y)\in x))\end{aligned} \]
ここで、\(S(y)\)は後継者順序的集合と呼ばれるものです。いわば「次の数」のようなものが、集合を使って作れます。
まずは順序数を簡単に説明しましょう。そのためには、順序を先に定義する必要があります。
集合\(A\)上の関係\(R\)は、推移律、反反射律、三択の比較可能性が成り立つとき、全順序(total order)と呼ばれます。\(<\)のような関係ですね。特に、全順序であって、\(A\)の空でない集合に関係\(R\)について必ず最小元が存在するとき、組\((A,R)\)は整列順序(well-ordering)である、または\(R\)は\(A\)を整列する(well-order)と呼ばれます。
集合\(x\)が順序的(ordinal)であるとは、関係\(\in\)によって整列されていて、推移的な集合であることです。\(x\)が推移的(transitive)であるとは、\(x\)のすべての要素が\(x\)の部分集合であること。
例えば、\( x=\{\emptyset, \{\emptyset\} , \{\emptyset, \{\emptyset\} \} \} \)は順序的です。例えば、\(\{\emptyset, \{\emptyset\} \}\)という要素は最初の2つの要素の和集合であるように、推移的です。そしてどんな部分集合を取っても、\(\in\)について最も小さい(=入れ子の少ない)要素が存在しますね。
(任意の整列集合に対して、それと順序同型な順序的集合が一意に定まります。順序的集合に入る順序は、ある意味で一意なわけですね。この証明には、置換の公理を用います。)
順序的集合が定義できれば、無限公理が理解できます。
順序的集合\(\alpha\)に対して、\(S(\alpha ):= \alpha \cup \{\alpha\}\)を後継者(successor)と呼びます。
無限の公理(infinity):\[ \begin{aligned}\exists x\, ( \emptyset \in x \land \forall y\in x(S(y)\in x))\end{aligned} \]
空集合\(\emptyset\)を含み、空集合の後継者を含み、その後継者を含み……、と限りなく続く、そういう集合\(x\)が存在すると言っています。
無限公理から、自然数の集合が定義できます。
順序的集合\(\alpha\)が自然数(natural number)であるとは、任意の順序的集合\(\beta \leq \alpha\)に対し、\(\beta =\emptyset \)であるか、\(\beta = S(\gamma)\)となる\(\gamma\)が存在すること。\(\beta \leq \alpha\)とは、\(\beta =\alpha\)または\(\beta \in \alpha\)のことです。
つまり、\(\alpha\)の要素となる集合(\(\alpha\)以下の数)がすべて、\(0 :=\emptyset\)であるか、\(0\)の後継者順序数\(1:= S(0),2:=S(1),\dots\)のいずれかとして表させるとき、\(\alpha\)を自然数と呼ぶわけです。
無限の公理により存在する\(x\)は、すべての自然数を含みます。よって、\(x\)の要素であり自然数である要素を集めた集合は、内包性の公理より存在し、それを自然数の集合\(\mathbb{N}\)と呼ぶわけです。(集合論の文脈では、\(\omega\)とも表記されます)
こうして作られた自然数の集合は、ペアノの公理を満たし、数学的帰納法の原理も満たします。そもそも、無限の公理の文\(( \emptyset \in x \land \forall y\in x(S(y)\in x))\)自体、帰納的(再帰的)な内容を表していますね。
冪集合の公理
冪集合の公理(power set):\[ \begin{aligned}\forall x \,\exists y \,\forall z(z \subset x \Rightarrow z \in y)\end{aligned} \]
これを用いれば、任意の集合\(x\)に対して、その冪集合(power set)
\[ \begin{aligned}\mathcal{P}(x) := \{z \mid z \subset x\}\end{aligned} \]
が定義できます。
僕は集合論を学び初めのとき、無限集合の冪集合なるものが登場して、果たしてそんなものが存在すると言えるのか少し不安だったのですが、それは公理によって定められた対象だったんですね。
集合の濃度について、カントールの定理\( \mathrm{card}(x) \leq \mathrm{card} (\mathcal{P}(x))\)が知られていたり、位相空間、測度空間(確率空間)の公理的な定義に冪集合を用いるように、冪集合は数学の様々なシーンで活躍しています。
基礎の公理
基礎の公理(foundation)、正則性の公理(regularity):\[ \begin{aligned}\forall x [\exists a \in x \Rightarrow \exists y(y \in x \land \lnot \exists z(z \in x \land z \in y))]\end{aligned} \]
集合論的な言葉を使えば、次と同値です。
\[ \begin{aligned}\forall x\, x\neq \emptyset \Rightarrow \exists y \in x (x \cap y =\emptyset)\end{aligned} \]
この公理は、いわゆる素朴集合論と呼ばれる話では、あまり明示的に登場しないかもしれません。
基礎の公理によると、すべての集合は、整礎的集合(well-founded set)になります。整礎的集合とは、ざっくり言えば、\(\emptyset\)から、その冪集合、和集合を取ることによって再帰的に構成される集合\(R(\alpha)\)です。
これをより明確に理解するために、次のような表記を考えましょう。
\[ \begin{aligned}\mathbf{V} := \{x \mid x=x\}\end{aligned} \]
\[ \begin{aligned}\mathbf{WF} := \bigcup \{R(\alpha) \mid \alpha \textrm{は順序的集合}\}\end{aligned} \]
これは「ある集合全体を集めたもの」であり、集合ではありませんが、クラス(class)と呼ばれる枠組みに入ります。
\(\mathbf{WF} \)は、\(\mathbb{R},\mathbb{C}\)、群や空間など代数的構造を持つ集合など、多くの数学的な対象を含んでいることが知られています。
さて、今まで述べてきた公理によると、\(x = \{x\}\)なる集合が存在する可能性があります。この\(x\)は整礎的ではありません(\(x \not \in \mathbf{WF} \))。そして、\(\mathbb{R},\mathbb{C}\)の構成にあたってもなお、\(x = \{x\}\)なる集合は用いなくて良く、整礎的集合で足りているのです。
ZFCから基礎の公理、選択公理を除いた公理系において、以下は同値
- 基礎の公理
- \(\mathbf{V} = \mathbf{WF}\)
つまり、普通の数学を考える上で、集合と言えば整礎的\(\mathbf{WF}\)なものに限って考え、そこでは\(x=x\)が成り立ち、\(x=\{x\}\)のような集合は除外されているわけです。
\(x=\{x\}\)のような集合を考えなくて良い公理という意味では、まさに数学の基礎となる公理と言えるのではないでしょうか。
選択公理
選択公理(choice):\[ \begin{aligned}\forall A\, \exists R\, (R \text{は} A \text{を整列する})\end{aligned} \]
すべての集合には、整列集合となるような順序関係が存在するという公理ですね。これは整列可能定理とも呼ばれます。
同値な文として
\[ \begin{aligned}\forall \mathcal{F} [ \emptyset \not \in \mathcal{F} \Rightarrow \exists f:\mathcal{F} \to \bigcup \mathcal{F}\, \forall A \in \mathcal{F} (f(A) \in A)]\end{aligned} \]
空でない任意の集合族には、そこから一斉に要素を取り出す関数(選択関数)が存在するという主張ですね。
選択公理は、この他にもZornの補題など、多くの命題と同値であることが知られています。
選択公理を仮定すると、バナッハ-タルスキーの定理が成立します。これは直観に反する結果(パラドックス)と呼ばれることがありますが、単なる定理です。
いわゆる普通の数学では選択公理は仮定されるかと思います(数理論理学では、もちろん選択公理を仮定しない数学や、選択公理と諸定理の関係性も考えるでしょう)。例えば僕が専攻していた解析学の分野では、関数解析学におけるハーン-バナッハの定理が選択公理によって示されます。
公理から導かれる結果
これまで述べてきた公理によって、数学は構成されます。
関係からは同値関係が定義でき、したがって同値類や商集合が定義できます。
写像を使えば、写像の全射、単射、濃度も定義できます。集合\(X\)上の数列も、\(f: \mathbb{N}\to X\)として扱えますね。
無限公理からその存在が言えた自然数の集合\(\mathbb{N}\)を使って、整数、有理数、実数、複素数の集合も構成できます。
長くなりましたが、集合論の公理として、ZFC公理系を紹介してきました。
そのどれもが、基本的な集合の存在または構成方法を示している文であることが、感じ取ってもらえたでしょうか。
数の集合や順序、関数といった数学では当たり前のように使う対象も、すべて集合として構成できる、そしてその基礎には形式言語を使った論理があるという話は、改めて見返すと良くできていて、面白いなと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
参考文献
Set Theory An Introduction To Independence Proofs
North Holland (1983-12-01)
売り上げランキング: 41,292
Set Theory: The Third Millennium Edition, revised and expanded (Springer Monographs in Mathematics)
Springer (2011-09-08)
売り上げランキング: 114,721
Mathematical Logic (Undergraduate Texts in Mathematics)
Springer (2012-12-12)
売り上げランキング: 179,586
売り上げランキング: 12,368
こちらもおすすめ
記号論理、命題論理入門:覚えるべき論理記号(否定、かつ、または、ならば、同値)とは
述語論理、量子化とは:全称記号(∀)と存在記号(∃)、数学における例と否定