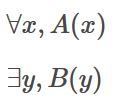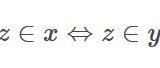形式言語、論理式、文とは：公理的集合論に向けて

どうも、木村（@kimu3_slime）です。

大学数学は集合論をベースにしていて、その基礎は公理的集合論によって与えられています。今回は、公理的集合論を紹介するために、その前段階である、形式言語、論理式について紹介します。

前提知識：集合論のはじまり、命題論理、述語論理、

集合論の基礎と記号論理
形式言語と論理式、文
こちらもおすすめ

集合論の基礎と記号論理

例えば、\(0\)以上\(1\)以下の数の集合は

\[ \begin{aligned}\{x\mid 0\leq x \leq 1\}\end{aligned} \]

と表されます。より一般に、集合とは「ある条件を満たすものの集まり」と、素朴には定義されます。例えば、\(A(x)\)を変数\(x\)を含む命題として

\[ \begin{aligned}\{x\mid A(x)\}\end{aligned} \]

という集合を考えるたいわけです。

しかし命題とは何でしょうか。真偽が定まる条件文というだけでは、制限が足りていないことが知られています。

その例が、ラッセルのパラドックス（Russel’s paradox）です。

\[ \begin{aligned}\{x\mid x \not \in x\}\end{aligned} \]

という集まりを考え、これを集合として扱うと、矛盾を導いてしまいます。

こちらで紹介しました：集合論入門：集合の定義、数の集合、ラッセルのパラドックス

つまり、「\(\{x\mid x \not \in x\}\)が集合である」という命題は偽です。集合を含み、集合論の規則にとらわれない集まりをクラス（class）と呼びます。すべての集合はクラスですが、ラッセルのパラドックスに登場するクラスは集合ではありません（このようなクラスを真のクラス proper class という）。

ラッセルのパラドックスは、集合論の土台を揺るがすようなものではありません。

公理的集合論（axiomatic set theory）では、集合とは何かを定める根本的なルール（公理）を、記号論理学の言葉で表現します。そこでは、ラッセルのクラスは集合と区別されるわけです。

今回の問題は、\(x \not \in x\)という文を、集合の定義

\[ \begin{aligned}\{x\mid A(x)\}\end{aligned} \]

に使ってしまったためです。ラッセルのパラドックス以外にも、ベリーのパラドックスやリシャールのパラドックスのように、普通の言葉（自然言語）で書かれたために矛盾を引き起こしてしまう、命題っぽく見える文が存在します。

そこで、集合を定義するために使う文\(A(x)\)とは何であるべきかを、記号論理学の枠組みを使って定義します（閉論理式）。そのために登場するのが形式言語で、それを使って論理式、文が定義されます。

文を使って、集合論の公理は記述されるのです。例えば今回の集合の定義に使う内包公理（comprehension scheme）は、\(z\)を「（外延性公理を満たす記号という意味での）集合」、\(\phi\)を任意の論理式として

\[ \begin{aligned}\exists y\, \forall x \,(x\in y \Leftrightarrow (x \in z) \land \phi )\end{aligned} \]

です。これがどういうものなのか知るために、形式言語の話をしましょう。

形式言語と論理式、文

公理的集合論を考えるときは、集合、自然数や実数などの計算法則や、文の真偽を知らないような立場から出発します（メタ数学）。つまり、僕たちが知っているのは意味を持たない文字、記号です。

たとえ\(1,2\)という文字が表れたとしても、それは記号にすぎず、計算は行なえません。ただし命題論理、述語論理の考え方・推論規則（1階述語論理）は既知としましょう。

言語

そして次のような記号の集まりを（1階の）形式言語（formal language）、または単に言語と呼びます。

論理接続詞、量化子：\(\lnot, \land, \forall\)（他の論理記号はこれらの組み合わせとして導けるので、ここに加わっていると考えて良い）
述語記号：\(\in,=\)
定数記号：\(0,1,2,\dots,\) （これは記号にすぎない）
変数記号：\(x_1, x_2, \dots\) （例えば\(x=x_1,y=x_2\)とすることで、ここから他の変数を導入できる）
句読点記号（カッコとカンマ）：\((,),”,”\)
（関数記号：\(+, \times\)）

特に上の言語を、特に集合論の言語と呼びます（考えたい状況に応じて、もう少し多くの記号を想定することがあります）。

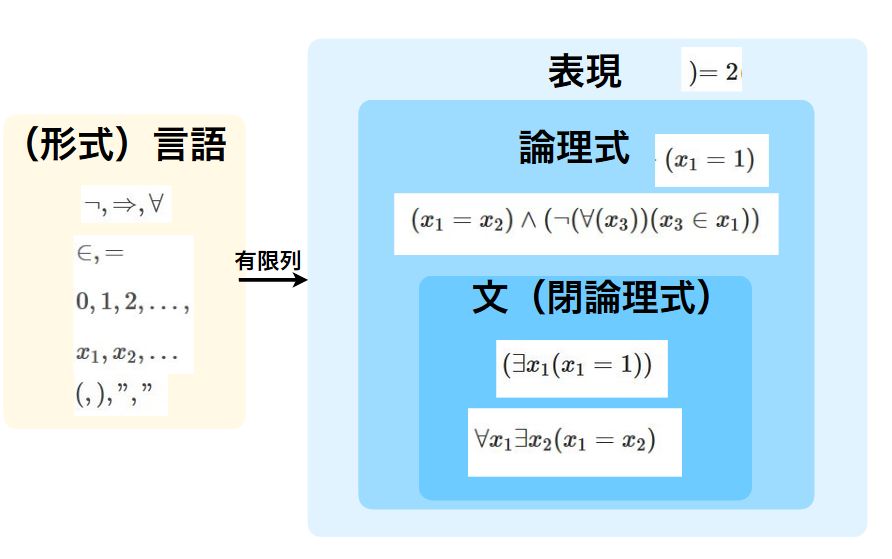
論理式

論理式は、表現と呼ばれる文字列から構成されます。

言語の表現（expression）とは、言語の記号を有限個並べた文字列です。例えば、\()=2\)は表現です。並べたものなら何でも良いわけですが、これには意味が設定できそうにありません。

そこで、論理式（formula）と呼ばれる表現を、次のように定義します。

どのような\(i,j\)に対しても、\(x_i \in x_j , x_i = x_j\)は論理式。
1の論理式\(\phi, \psi\)を使って表される、\(\lnot (\phi), (\phi) \land (\psi), \forall x_i (\psi)\) は論理式。

1の論理式を、原子論理式（atomic formula）と呼びます。原子論理式を規則にしたがって組み合わせた表現、例えば

\((x_1 =x_2) \land (\lnot (\forall (x_3)) (x_3 \in x_1 ))\)

は論理式と呼べるわけです。ここには登場しなかった論理記号\(\lor, \Rightarrow, \Leftrightarrow, \exists\)なども、\(\lnot, \land, \forall\)の組み合わせとして表せます。

なので、例えば\(\exists x_i(\phi)\)は、\(\lnot( \forall x_i(\lnot (\phi)))\)の省略として扱えます。こうして、原子論理式を論理接続詞を使って組み合わせたものは、論理式と言えます。

自由変数、束縛変数

\[ \begin{aligned}\phi :\Leftrightarrow (x_1 =1)\end{aligned} \]

\[ \begin{aligned}\psi :\Leftrightarrow( \exists x_1 (x_1 =1))\end{aligned} \]

はどちらも論理式ですが、\(\phi\)にはその真偽が定まりそうになく、\(\psi\)には定まりそうです。

論理式に登場する変数が束縛されている（bounded）とは、その変数がその変数に作用する量化子の範囲（scope）に入っていること。その範囲に入っていないときは、変数は自由である（free）と言います。

\(\phi\)においては\(x_1\)は自由変数ですが、\(\psi\)においては束縛変数というわけです。変数の束縛は量化子によって起こり、他の論理記号では起こりません。

論理式に登場する変数を\(\phi(x_1,x_2,x_3)\)のように明示すると、依存関係が明確になり便利です。たいていはこう書くときは\(x_1,x_2,x_3\)は自由変数ですが、束縛変数であることや、登場しない可能性もあります。

文

どうやら、束縛変数のみを持つ論理式には、真偽が定まりそうです。

文（sentence）とは、自由変数を持たない論理式のことです。文は閉論理式（closed formula）とも呼ばれます。これが普通の数学で言う、条件や命題と呼ばれるものに対応します。

例えば、

\[ \begin{aligned}\forall x_1 \exists x_2 (x_1 =x_2)\end{aligned} \]

は文です。集合論の公理系は、特定の文の集まりからできています。

文が論理的に同値、妥当である

文には、真偽が定まります。つまり、ある文から別の文を導いて（演繹して）、意味を定めることができるのです。

\(S\)を文の集まり、\(\phi\)を文として、\(S\)から\(\phi\)が証明できる（provable）\(S \vdash \phi \)とは何か、定義しましょう。

\(S \vdash \phi\)とは、\(\phi\)の\(S\)からの形式的な演繹（formal deduction）が存在することとします。

形式的演繹とは、次のようなものです。次のような論理式の有限の列\(\phi_1,\dots, \phi_n\)が存在すること。\(\phi _n \)は\(\phi\)です。そして、すべての\(i\)に対して、\(\phi _i\)は\(S\)に含まれるか、\(\phi_i\)は論理的な公理か、\(\phi_i\)はそれ以前の\(\phi_1,\dots,\phi_{i-1}\)から論理的に推論されるか。

つまり、\(S \vdash \phi\)というのは、\(S\)の文か公理から出発して、それらを使って論理的に推論していくことで、有限回で\(\phi\)にたどり着けるという意味ですね。（推論の規則については別の記事で？）

そして、\(S\)が何の文字列でもない（0個の文字列のとき）、\(S\vdash \phi\)を単に\( \vdash \phi\)と書き、論理式\(\phi\)は論理的に妥当（logically valid）であると言います。何の前提もなしに証明されることを、「正しい」と約束するわけですね。

さらに、2つの論理式\(\phi,\psi\)は、\(\vdash (\phi \Leftrightarrow \psi)\)が成り立つとき、論理的に同値である（logically equivalent）と言います。

ここまでくれば、集合論の公理を文の集まりとして用意し、そこから論理的に妥当な文を導いていくことができます。

今回は、ラッセルのパラドックスに登場する「文」を例にして、公理的集合論、形式言語の必要性を紹介しました。

妥当な文を作り出すためには、まず言語と呼ばれる記号の集まりから出発し、論理式、文（閉論理式）を定義します。

そして文と文の間の意味的な関係、文が証明できるとは、同値であるとはどういうことか、紹介してきました。

新しい記号や考え方が多く、戸惑ったかもしれません。公理的集合論に触れてみて、文の扱い方を知ることで、馴染みやすくなるでしょう。

公理的集合論の入門は、別の記事で紹介します：公理的集合論をわかりやすく解説：ZFC公理系を例に

木村すらいむ（@kimu3_slime）でした。ではでは。