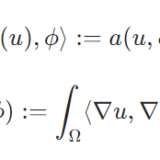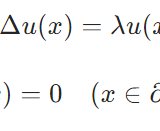正値作用素とは：例、固有値が正となることの証明

どうも、木村（@kimu3_slime）です。

今回は、正値作用素とは：例、固有値が正となることの証明を紹介します。

定義
例
- 正定値行列
- ラプラシアン
固有値が正となること
こちらもおすすめ

定義

コンパクトな対称作用素の固有値は可算個の実数列であるとわかりますが、その固有値がすべて正であると、\(\lim_{n \to \infty}\lambda_n\)と単調に増えるように並べられてより便利です。そのような性質を与える作用素の分類が、正値作用素です。

\(H\)をヒルベルト空間とし、線形作用素\(F:D(F)\to H\)について考えます。

\(F\)が正値作用素（positive operator）であるとは、「すべての\(u \in D(F)\)に対し、\(\langle F(u),u\rangle_H \geq k \|u\|_H^2\)」を満たす\(k>0\)が存在することです。

例

正定値行列

非常に簡単な例ですが、対角行列

\[ \begin{aligned}A = \begin{pmatrix} 2 & 0\\0&1 \end{pmatrix}\end{aligned} \]

によって決まる線形作用素\(A: \mathbb{R}^2 \to \mathbb{R}^2\)は、正値作用素です。実際、

\[\begin{aligned} &\langle Ax,x\rangle_{\mathbb{R}^2} \\ &= 2x_1^2+x_2^2 \\& \geq x_1^2+x_2^2\\&= 1\cdot \|x\|_{\mathbb{R}^2}^2 \end{aligned}\]

となり、\(k=1\)は\(x\)に依存していません。

一般に、対称な正定値行列（すべての\(x \in \mathbb{R}^N\)に対し、\(x \neq 0 \)ならば\(x^\top Ax >0\)）は正値作用素です。

行列\(A\)は連続性、内積の連続性から、二次形式\(f(x)= \langle Ax,x\rangle\)は連続です。したがって、\(B(0,1)=\{x \in \mathbb{R}^N \mid \|x\|=1\}\)という有界な閉集合上で最小値を持ちます。そして\(k:=\min _{\|x\| =1} \langle Ax,x\rangle>0 \)です。もし\(k=0\)とすると、正定値行列であることに矛盾するので（背理法）。

\(x=0\)のとき、\(A\)の線形性、内積とノルムの正定値性から、\(\langle Ax,x\rangle_H \geq k \|x\|_H^2\)は両辺を0として成り立ちます。

\(x \neq 0\)のときは、行列の線形性、内積の線形性、\(k\)が最小値であることから

\[\begin{aligned} &\langle Ax,x\rangle_{\mathbb{R}^N} \\ &= \|x\|^2 \langle A(\frac{1}{\|x\|}x),\frac{1}{\|x\|}x\rangle \\ &\geq k \|x\|^2\end{aligned}\]

となります。よって、正値作用素となることが示せました。

つまり、正値作用素は正定値行列を一般化したものとして見ることができるわけです。

ラプラシアン

弱形式のラプラシアン\(A=-\Delta\)は、正値作用素の例です。

\(A:H_0^1(\Omega)\to H^{-1}(\Omega)\)で、\(\phi \in H_0 ^1 (\Omega)\)に対し、

\[\langle A(u),\phi \rangle := a(u,\phi)\]

\[a(u,\phi):=\int_\Omega \langle \nabla u, \nabla \phi \rangle dx \]

という定義です。

したがって、

\[\begin{aligned} &\langle A(u),u \rangle \\ &= a(u,u) \\&= \int_\Omega \langle \nabla u, \nabla u \rangle dx \\&= \int_\Omega |\nabla u|^2 dx\\&= \|\nabla u\|_{L^2}^2\\&= 1\cdot \|u\|_{H_0^1}^2\end{aligned}\]

となるので、正値作用素です。ここで\(H_0^1\)のノルムは、ポアンカレの不等式から簡略化したものを用いています。