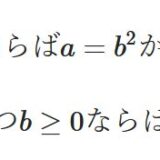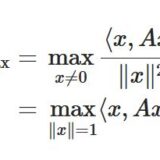2次形式、正定値行列とは：2変数関数の極値判定を例に

どうも、木村（@kimu3_slime）です。

今回は、2次形式、正定値行列とは何か、2変数関数の極値判定を例に紹介します。

2変数関数の極値と2次形式
正定値行列とは
こちらもおすすめ

2変数関数の極値と2次形式

（2変数の）2次形式（quadratic form）とは、2次の項のみからなる2変数の多項式関数です。2次関数を一般化したようなものと言えるでしょう。

\[ \begin{aligned}f(x,y)=ax^2+bxy+cy^2\end{aligned} \]

例えば、\(a=1,b=0,c=1\)のときは、\(f(x)=x^2+y^2\)となります。

参考：2変数関数と偏微分：グラフ、接平面を描いてみよう

2次形式は、行列と内積を使って表すことができます。（記号の重複がありますが）\(x=(x,y)\)とするとき、

\[ \begin{aligned} ax^2+2bxy+cy^2&= \begin{pmatrix}x \\y \end{pmatrix} \begin{pmatrix} ax+by\\bx+cy \end{pmatrix} \\&=\begin{pmatrix}x \\y \end{pmatrix} \begin{pmatrix} a&b\\b&c \end{pmatrix} \begin{pmatrix} x& y \end{pmatrix}\\&= x^\top Ax \\&= \langle x,Ax\rangle\end{aligned} \]

となるので。つまり、二次形式の取る値を調べるには、係数を並べた行列\(A\)がどんな性質を持つか（正定値行列かどうか）が重要になってきます。

\(A\)を2次形式の係数行列と呼びましょう。

2次関数を考える動機のひとつには、2変数関数の極値（最大値や最小値）を求める問題があります。

2変数関数を極値点\(p_0\)のまわりでテイラー展開すると

\[ \begin{aligned}f(p)\simeq f(p_0)+\frac{1}{2}\langle (p-p_0) , H(f)(p-p_0) \rangle\end{aligned} \]

\[ \begin{aligned}H(f) = \begin{pmatrix} f_{xx} & f_{xy}\\f_{yx}&f_{yy} \end{pmatrix}\end{aligned} \]

と2次形式が表れます。ここで\(f\)の2階偏微分を並べた係数行列\(H(f)\)は、ヘッセ行列と呼ばれるものです。

参考：2変数関数の極値の求め方、ヘッセ行列とは？

例えば、\(f(x)=x^2+y^2\)ならば、

\[ \begin{aligned}H(f) = \begin{pmatrix} 2 & 0\\0&2 \end{pmatrix}\end{aligned} \]

で、\(p_0=(0,0)\)でのテイラー展開は\(f(x)=\frac{1}{2}\langle x,H(f)x \rangle =\langle x,x\rangle\)となります。

内積の正定値性から、\(\langle x,x\rangle \geq 0\)なので、\(p_0=(0,0)\)が極小点であるとわかりますね。

この例では判定が簡単です。一般に、ヘッセ行列はさまざまな成分を持っていますが、その行列が持つ性質によって、極値点かどうか判定することはできないのでしょうか。それは実際できて、それが以降に紹介する正定値行列という考え方になります。

2次形式は、楕円、双曲線、放物線といった2次曲線（quadratic curve）や2次局面を調べるためにも利用されます。

例えば、楕円の方程式\(\frac{x^2}{4}+y^2=1\)は

\[ \begin{aligned} f(x,y)&= \frac{1}{4}x^2 +1 y^2\\&= x^\top \begin{pmatrix} \frac{1}{4}&0\\0& 1 \end{pmatrix} x\\&= 1\end{aligned} \]

と表されます。2次形式に対応する行列

\[ \begin{aligned}\begin{pmatrix} a&b\\b&c \end{pmatrix} \end{aligned} \]

は対称行列なので（\(xy= yx\)なので係数がまとめられる）、対角化可能です。

一般に、2次曲線

\[ \begin{aligned}ax^2+2bxy+cy^2+px+qy+r=0\end{aligned} \]

がどんな形をしているのかは、見た目からすぐには判別しにくいです。しかし、その係数行列を対角化すると

\[ \begin{aligned}\lambda_1X^2+\lambda_2Y^2+p’X+q’Y+r=0\end{aligned} \]

と\(xy\)を含まない形（2次曲線の標準形）にできます。これによって、楕円、双曲線、放物線なのかが明確になるわけです。

正定値行列とは

ここからは、係数行列と2次形式の持つ性質との関係に注目していきましょう。

定義

\(A\)を\(N\)次の対称行列とします。

\[ \begin{aligned}f(x) =x^\top Ax= \langle x ,Ax\rangle\end{aligned} \]

を\(N\)次の2次形式と呼びます。

行列と内積の性質から、\(f(0)=0\)を必ず満たします。

さきほどまでは2変数のケースのみを考えていましたが、\(N\)変数でも同様の理論が展開できます。2次の関数を考えることと、変数の数は混同しやすいので注意しましょう。

\(A\)が正定値行列（positive definite matrix）であるとは、すべての\(x \in \mathbb{R}^N\)に対し、\(x \neq 0 \)ならば\(x^\top Ax >0\)が成り立つことです。

\(A\)が負定値行列（negative definite matrix）であるとは、すべての\(x \in \mathbb{R}^N\)に対し、\(x \neq 0 \)ならば\(x^\top Ax <0\)が成り立つことです。

\(A\)が半正定値行列（positive semidefinite matrix）であるとは、すべての\(x \in \mathbb{R}^N\)に対し、\(x^\top Ax \geq 0\)が成り立つことです。

\(A\)が半負定値行列（negative semidefinite matrix）であるとは、すべての\(x \in \mathbb{R}^N\)に対し、\(x^\top Ax \leq 0\)が成り立つことです。

それぞれの条件が満たされるとき、\(A>0\)、\(A<0\)、\(A\geq 0\)、\(A \leq 0\)と不等号を使って書くことがあります。数の不等号とは違って、行列としての定値性を表すので注意。

\(A\)が正定値行列と単に呼ばれるときでも、暗に\(A\)が対称行列であることが前提とされています。正定値でなく、正値という用語を使うこともあります。文脈に応じて、用語の意味を読み取りましょう。

例

例えば、さきほど見たように、\(f(x,y)=x^2+y^2\)のヘッセ行列

\[ \begin{aligned}H(f) = \begin{pmatrix} 2 & 0\\0&2 \end{pmatrix}\end{aligned} \]

は正定値行列です。単位行列やその正の定数倍は正定値行列になります。

別の簡単な例として、

\[ \begin{aligned}-I =\begin{pmatrix} -1 & 0\\0&-1 \end{pmatrix}\end{aligned} \]

は負定値行列です。

\[ \begin{aligned} x^\top (-I)x = – \langle x,x \rangle \end{aligned} \]

となるので、内積の正定値性からわかりますね。

正定値行列の和、正のスカラー倍もまた、正定値行列になります。\(A,B\)を正定値行列、\(\lambda>0\)をスカラーとすると、\(x \neq 0\)ならば

\[ \begin{aligned} \langle x, (\lambda A+B)x \rangle&= \langle x,\lambda Ax+ Bx\rangle \\ &= \lambda \langle x,Ax \rangle+\langle x, Bx \rangle \\ &>& 0\end{aligned} \]

となるので、\(\lambda A+B\)は正定値行列です。

初学者が勘違いしやすいのですが、すべての行列が正定値行列または負定値行列であるわけではありません。

例えば、ゼロ行列\(O\)は正定値行列でも負定値行列でもありません。ただし、半正定値行列であり半負定値行列でもあります。これは数としてのゼロ\(0\)が正の数でも負の数でもないのと同じ理屈ですね。

さらに後で見るように、

\[ \begin{aligned} \begin{pmatrix} 1&0\\0 &-1 \end{pmatrix}\end{aligned} \]

という正負の固有値を併せ持つ行列は、半正定値行列でも半負定値行列でもありません。このような行列は、不定値行列（indefinite matrix）と呼ばれます。

数については\(a \geq 0\)または\(a \leq 0\)は常に正しいですが、行列については\(A \geq 0\)または\(A \leq 0\)とは言えないので注意しましょう。（半順序ではあるが、全順序ではない）

他の例としては、射影行列や（可逆な正方行列の）グラム行列は半正定値行列であると知られています。

\[ \begin{aligned} \langle x,A^\top A x\rangle &=x^\top A^\top Ax\\ &= (Ax)^\top Ax \\&= \langle Ax,Ax\rangle\\ & \geq 0\ \end{aligned} \]

特に、対称な正方行列のグラム行列は\(A^2\)であり、それは常に半正定値行列となります。これはすべての数\(a\)は2乗すると0以上\(a^2 \geq 0\)に似た結果ですね。

（実は、逆：「\(A\)が正定値行列ならば、\(A=B^2\)となる正定値行列\(B\)が存在する」も正しいです。これを行列の平方根と呼び、\(B = \sqrt {A}\)と表します。）

同値な定義、判定法

正定値行列の考え方は、2次形式の極値を調べるのに便利そうではありますが、どうやって行列が正定値かどうか判定したら良いのでしょうか。

そこで正定値であることと、同値な条件がいくつか知られています。

\(A\)を対称行列とする。そのすべての固有値は実数となる。

次の条件は同値。

\(A\)が正定値行列である
\(A\)の固有値がすべて正である
\(A\)のすべての主小行列式（左上から\(1,2,\dots\)次の正方行列を取り出した小行列\(A_k\)の行列式）が正である \(\det A_k >0\)
\(B\)を列ベクトルはすべて線形独立である行列として、\(A= B^\top B\)と表せる
コレスキー分解（Cholesky decomposition）：\(C\)を上三角行列として\(A=C^T C\)と表せる

負定値、半正定値、半負定値行列についても、不等号を置き換えて同様の主張が成り立つ。

簡単のため、1番と2番の同値性のみ示します。他のケースは「ストラング:線形代数イントロダクション」と齋藤「線型代数入門」を参照してください。

1から2。\(\lambda \)が固有値であるとは、\(Ax =\lambda x, x\neq 0\)が成り立つことでした。この両辺で\(x\)との内積を取れば、

\[ \begin{aligned} \langle x, Ax \rangle &= \langle x,\lambda x \rangle \\ &= \lambda \langle x,x\rangle \\ &>& 0 \end{aligned} \]

となります。\(x \neq 0\)なので、内積の正定値性から\(\langle x,x\rangle \neq 0\)であり、\(\lambda >0\)が得られました。

2から1。対称行列は直交行列により対角化可能なので、\(P\)を直交行列、\(D\)を固有値が並んだ対角行列として、\(P^{-1}AP=D\)と表せます。仮定より\(D\)の対角成分はすべて正なので、すべての\(y \neq 0\)に対して、\(y^\top P^{-1}AP y = y^\top D y >0\)が成り立ちます。任意に\(x\)、\(x \neq 0\)を選びましょう。そして\(y=P^{-1}x\)と置くと、\(x \neq 0 \)なので\( y \neq 0\)です（可逆行列の全単射性）。また、\(x^\top =(Py)^\top =y^\top P^\top=y^\top P^{-1}\)です（\(P\)は直交行列なので\(P^\top = P^{-1}\)）。したがって、さきほどの等式から\(x^\top A x >0\)が言えました。

正定値行列と同値な条件を使えば、2変数の極値を、ヘッセ行列の固有値（または小行列式＝成分）を使って判定できますね。

参考：2変数関数の極値の求め方、ヘッセ行列とは？

以上、2次形式をなぜ考えるかを極値問題を例に述べ、正定値行列について紹介してきました。

今回は実成分で考えたが、複素成分でも同様の理論が成り立ちます。

対称行列は対角化することでシンプルになりますが、それによって2次形式を簡単な形：標準形に変形できます。そしてその係数の正負の個数は一定である：シルベスターの慣性法則という主張があります。これについては別の機会紹介するかもしれません。

また、今回紹介した2次形式は、双線形形式とも呼ばれ、多重線形形式と呼ばれる一般化された理論があります。関数解析では、関数空間における双線形形式を扱うでしょう（ラックス・ミルグラムの定理）。多様体論では微分形式という概念を扱いますが、その基礎としても2次形式を知っておくと良いでしょう。

2次形式とは簡単に言えば多変数の2次関数のようなものですが、それを線形代数の理論：正定値行列として調べられるのは面白いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。