どうも、木村(@kimu3_slime)です。
高校数学以降では、複素数の扱いを学びます。
実数では\( 0 < 1\)といったように大小比較ができますが、複素数ではそのような比較を考えません。それはなぜでしょうか。
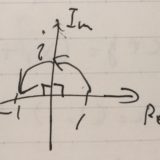
簡単に言えば、仮に\(0 <i\)というような順序関係があったとすると、両辺に\(i\)をかけると\( 0 < -1\)となってしまうからです。
今回は、複素数では「普通の」順序・不等号を定義できないことを紹介します。
順序とは何か
数同士の大小関係は、\(<, \leq \)といった不等号を使って表記します。
不等号のように、2つの間の順序を決める記号(演算)は、数学では順序関係(order relation)と呼ばれています。
順序関係とは
普通の数、整数や実数には順序が定まっています。
例えば、次のようなことが成り立っていますね。\( 1 \leq 1\)です。\( 1 \leq x \)かつ\(x \leq 1\)ならば\(x=1\)です。\(x \leq 1\)かつ\(1 \leq y\)ならば\( x \leq y\)です。どんな数に対しても、\(x \leq y \)か\( y \leq x\)のいずれかが成り立ちます。
これらの性質をまとめると、次のようになります。一般に、\(X\)を集合として、
- (1) 反射律: すべての\(x\in X\)に対して、\(x \leq_X x\)
- (2) 反対称律: すべての\(x,y \in X\)に対して、\(x \leq_X y\)かつ\( y \leq_X x\)ならば\(x=y\)
- (3) 推移律:すべての\(x,y,z \in X\)に対して、\(x \leq_X y\)かつ\(y \leq_X z\)ならば\( x\leq_X z\)
- (4) 比較可能: すべての\(x,y \in X\)に対して、\(x \leq_X y\)または\( y \leq_X x\)のいずれかが成り立つ。
を満たすような2項関係\( \leq_X\)を、全順序関係と言います。
さらには、整数や実数では足し算や掛け算を考えることができ、それと関連した不等式の性質があります。
例えば、\(x \leq 1\)ならば、マイナスの数をかけると\( -x \geq -1\)と逆向きになります。これは\(x \leq 1\)の両辺に\(-x-1\)を加えたと見て取れるものです。またプラスの数をかけても順序は変化せず、\(x\leq 1\)ならば\(3 x \leq 3\)となります。
- (5)和との両立: すべての\(x,y,z \in X\)に対して、\(x \leq_X y\)ならば\(x+z \leq_X y+z\)
- (6)積との両立: すべての\(x,y,z \in X\)に対して、\(x \leq_X y\)かつ\(0 \leq_X z\)ならば\(z x \leq_X zy\)
です。これが満たされるとき、順序と演算(和、積)が両立していると呼ばれます。また、これらを満たす和と積の定義された集合\(X\)は、順序環、順序体と呼ばれます。整数は順序環であり、実数は順序体です。
複素数に「普通の」順序が定まらないこと
複素数\(\mathbb{C}\)では、普通は和や積が考えられています。つまり複素数の集合は体となります。しかし、その和や積と両立するような順序は存在しません。すなわち、順序体とならないことを示しましょう。
仮に、上記の順序の条件(1),…,(6)を満たし、実数に対しての順序を保つような複素数の順序関係\(\leq _{\mathbb{C}}\)があったとしましょう。
注目すべきポイントは、和、積との両立条件と虚数単位\(i\)を使った計算をすると、破綻を導いてしまうということです。
比較可能性(3)より、\(0 \leq _{\mathbb{C}} i \)か\( i\leq _{\mathbb{C}} 0\)のいずれかが成立します。場合分けして示しましょう。
- 仮に、\(0 \leq _{\mathbb{C}} i \)であったとします。積との両立条件より、両辺に\(i\)をかけると、\( 0 \leq _{\mathbb{C}} -1\)となります。これは実数の順序関係と矛盾します。
- 仮に、\( i\leq _{\mathbb{C}} 0\)であったとします。和との両立条件より、両辺に\(-i\)を加えると\(0 \leq _{\mathbb{C}} – i\)です。したがって、両辺に\(- i\)をかける、積との両立条件を\(-i \)を使うと、\( 0 \leq _{\mathbb{C}} (-i)(-i)\)となる。\((-i)(-i) = i^2 =-1\)なので、\( 0 \leq _{\mathbb{C}} -1\)。これは実数の順序関係と矛盾。
いずれにせよ矛盾が導かれるので、実数の順序を保ち、和と積の両立条件を満たすような複素数の順序\(\leq _{\mathbb{C}}\)は存在しないことがわかりました。
複素数でも順序を考えること自体はできる
実は、条件を落とせば、複素数に対しても「順序」を定めること自体はできます。
複素数の集合を\(\mathbb{C}\)とします。\(z=x_1+y_1 i ,w =x_2 +y_2 i \in \mathbb{C} \)に対して、\( \leq _1\)という2項関係を次のように定めましょう。
\(z \leq _1 w\)とは、「\(x_1 <x_2\)」または「\(x_1 =x_2\)かつ\(y_1 \leq y_2\)」であると。つまり、まずは実部を比較して順序を決める。もし実部が等しいなら、虚部によって順序を決めるという順序です。
例えば、\(2+5i \leq_1 3 +2i\)で、\(3-3i \leq_1 3 +i \)です。複素数に順序を考える……といって単純に想像しやすそうな性質ですね。
\( \leq _1\)が全順序関係となることを確かめてみましょう。
- (1) 反射律: すべての\(z \)に対し、\(x_1 = x_1\)と\(y_1 \leq y_1\)を満たすので、\(z \leq_1 z\)は成り立ちます。
- (2) 反対称律: \(z \leq_1 w\)かつ\( w \leq_X z\)と仮定します。\(x_1 <x_2\)のパターンはありえず、\(x_1=x_2\)となります。\(y_1 \leq y_2\)かつ\(y_2 \leq y_1\)なので、\(y_1 =y_2\)が成り立ちます。よって、\(z=w\)が成り立ちました。
- (3) 推移律:すべての\(z_1,z_2,z_3 \in X\)に対して、\(z_1 \leq_1 z_2\)かつ\(z_2 \leq_1 z_3\)としましょう。
- \(x_1 < x_2 \)かつ\(x_2< x_3\)のときは、\(x_1 <x_3\)なので、\(z_1 \leq_1 z_3\)です。
- \(x_1=x_2\)かつ\(x_2 < x_3\)のとき。\(x_1 <x_3\)なので、\(z_1 \leq_1 z_3\)です。
- \(x_1=x_2\)かつ\(x_2 =x_3\)のとき。\(\leq_1\)の定義より、\(y_1 \leq y_2\)かつ\(y_2 \leq y_3\)で、したがって\(y_1 \leq y_3\)となる。よって、\(z_1 \leq z_3\)となりました。
- (4) 比較可能: \(z,w \in X\)とします。実部について場合分けすると、\(x_1 <x_2\)、\(x_2 <x_1\)、\(x_1=x_2\)の3つの可能性があります。
- \(x_1 <x_2\)のときは、\(z \leq_1 w\)で、\(w \leq 1 z\)は成り立ちません。
- \(x_2 <x_1\)のときも同様です。
- \(x_1=x_2\)のときは、\(y_1 \leq y_2\)または\(y_1 > y_2\)のいずれか一方が成り立ちます。\(y_1 \leq y_2\)のときは\(z \leq_1 w\)で、\(y_1 > y_2\)のときは\(w \leq _1 z \)です。比較可能性が言えました。
このような全順序\(\leq_1\)は、辞書式順序と呼ばれるものです。
複素数でも、全順序という順序を考えること自体はできるのです。しかし、普通の順序=和と積と両立するような順序を考えることはできない、そういうものがあったとすると矛盾するというのが今回の話でした。
ちなみに、ベクトルに対しても辞書式順序を考えることはできます。しかし、演算と両立するような順序……と議論しようとすると、ベクトルではそもそも良い「積」を考えられません。ベクトルの内積は実数を返し、ベクトルを返さないです。外積はベクトルを返しますが、交換法則や結合法則を満たしません。
以上、複素数では普通の順序・不等号・大小関係を考えないのはなぜか、紹介してきました。
整数や実数で考えていたような、和と積と両立させる性質を持った順序を考えることはできない、というのが理由です。
辞書的順序という順序自体を考えることはできますが、それは全順序止まりで、演算と両立した順序になりえません。「普通」の順序・大小関係を定義しようがないわけです。
複素数に何か順序を導入できないか、という発想自体は面白いものだと思います。ただ、和や積との両立条件まで成り立つような順序が存在しないということについて、今回の話を思い出してもらえれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-07T00:00:01Z)
¥7,607 (コレクター商品)