どうも、木村(@kimu3_slime)です。
今回は、同値関係、2項関係とは何か、整数の合同(mod)を例に紹介します。
等号の性質
同値関係とは、おおざっぱに言えば、等号\(=\)の持つ性質の一般化です。
\(X\)を集合とする。
- 反射律:すべての\(x \in X\)に対して、\(x=x\)が成り立つ
- 対称律:すべての\(x,y \in X\)に対して、\(x=y\)ならば\(y=x\)が成り立つ
- 推移律:すべての\(x,y,z \in X\)に対して、\(x=y\)かつ\(y=z\)ならば、\(x=z\)が成り立つ。
これは等式の性質の一部であり、\(x,y,z\)を数とすれば当たり前に成り立っているもの、と考えられるような規則です。
等号\(=\)に限らず、この3つの関係性を満たすような規則を、同値関係と呼びます。(詳しくはまた後で)
整数の合同が同値関係であること
同値関係の例として、整数の合同関係を考えましょう。
2つの整数\(x,y\)の差\(x-y\)がある整数\(n\)の倍数であるとき、\(x,y\)は\(n\)を法として合同(congruent modulo \(n\))と呼び、\(x\equiv y\, (\mathrm{mod}\, n)\)と表します。
例えば、\(8\equiv 4\, (\mathrm{mod}\, 2)\)です。なぜなら、\(8-4 =4=2\times 2\)なので。また、\(25\equiv 10\, (\mathrm{mod}\, 5) \)です。なぜなら、差は\(15=5\times 3\)なので。
合同でないときは、\(\not \equiv\)を使います。\(2\not \equiv 9\, (\mathrm{mod}\, 2)\)です。その差は、\(9-2=7=2\times 3+1\)だから。何を法とするかによって、合同かどうかは変わることに注意しましょう。差は\(7\)なので、\(2 \equiv 9\, (\mathrm{mod}\, 7)\)です。
簡単のため、\(x\equiv y\, (\mathrm{mod}\, n)\)を\(x \equiv _n y \)と表すことにします。このようにして定義された整数の合同\(\equiv _n\)が、
- 反射律:すべての\(x \in \mathbb{Z}\)に対して、\(x\equiv _n x\)が成り立つ
- 対称律:すべての\(x,y \in \mathbb{Z}\)に対して、\(x \equiv _n y\)ならば\(y\equiv _n x\)が成り立つ
- 推移律:すべての\(x,y,z \in \mathbb{Z}\)に対して、\(x\equiv _n y\)かつ\(y\equiv _n z\)ならば、\(x=z\)が成り立つ。
という性質を満たすことを確かめましょう。 \(\mathbb{Z}\)は、整数全体の集合です。
反射率について。\(x\in \mathbb{Z}\)と仮定します。すると、\(x – x = 0 = n\cdot 0\)なので、\(x\equiv _n x\)が成り立ちます。
対称律について。\(x,y\in \mathbb{Z}\)で、\(x \equiv _n y\)と仮定します。合同関係の定義より、\(x-y = nk\)となる\(k \in \mathbb{Z}\)が存在します。等式にマイナス1をかけると、\(y-x = n(-k)\)が成り立ちます。よって、\(y \equiv _n x\)が成り立つことがわかりました。
推移律について。\(x,y,z \in \mathbb{Z}\)で、\(x\equiv _n y\)かつ\(y\equiv _n z\)と仮定します。合同関係の定義より、\(x-y = nk\)、\(y-z = n\ell\)を満たす\(k,\ell \in \mathbb{Z}\)が存在します。この2つの等式の和を考えると、\(x-z = nk+n\ell= n(k+\ell)\)が成り立ちます。\(k,\ell \in \mathbb{Z}\)なので\(k+\ell \in \mathbb{Z}\)であり、\(x\equiv _n z\)であることがわかりました。
2項関係、同値関係とは
今までの議論を、より一般的な視点から整理しましょう。
等号\(=\)や整数の合同\(\equiv\)は、常に2つの数・要素を対象にしています。こうした2つの要素を対象にした記号を、一般に\(\sim\)と表してみましょう。
等号や整数の合同では、常に\(x=y\)か\(x \neq y\)のいずれかが成り立ちます。そこで、\(X\)を集合として、その任意の2つの要素\(x,y\in X\)に対して、\(x \sim y\)が真偽の定まった命題であるとき、\(\sim \)を2項関係(binary relation)と呼びます。
(さらなる一般的な議論として、2項関係は直積集合\(X\times Y\)の部分集合\(R\)としても定義されます。つまり、\((x,y ) \in R\)を\(x\sim y\)、\((x,y) \notin R\)を\(x\sim\)と捉えるわけです。集合間の写像・関数は、2項関係の一種として一般的に定義できます。)
2項関係\(\sim\)が、
(E1)反射律:\(\forall x \in X \quad x\sim x\)
(E2)対称律:\(\forall x,y \in X \quad x\sim y\)ならば\(y \sim x\)
(E3)推移律:\(\forall x,y,z \in X \quad x\sim y,y\sim z\)ならば\(x\sim z\)
を満たす時、同値関係(equivalence relation)呼びます。
上で確かめたことによって、整数の合同\(\equiv_n \)は\(\mathbb{Z}\)上の同値関係となります。
同値関係からは、いくつかの要素を同一視する同値類と呼ばれる考えが生まれ、商集合や商群の定義に用いられています。
すべての2項関係が同値関係であるわけではありません。
整数\(\mathbb{Z}\)において、不等号\(\leq \)を考えてみましょう。\(x \leq y\)は成り立つか成り立たないかが決まり、これは2項関係です。
そして、反射律と推移律は成り立ちます。\(x \leq x\)は常に正しいです。また、\(x\leq y, y\leq z\)のとき、\(x \leq z\)が成り立ちます。
しかし、対称律\(x \leq y\)ならば\(y \leq x\)は一般には成り立ちません。例えば、\(0 \leq 1\)のとき、\(1 \leq 0 \)は誤りです。
その代わりに、「\(x \leq y\)かつ\( y \leq x\)ならば、\(x=y\)」という反対称律と呼ばれる性質が成り立っています。こうした不等号の性質を取り出した関係は、順序関係と呼ばれるものです。
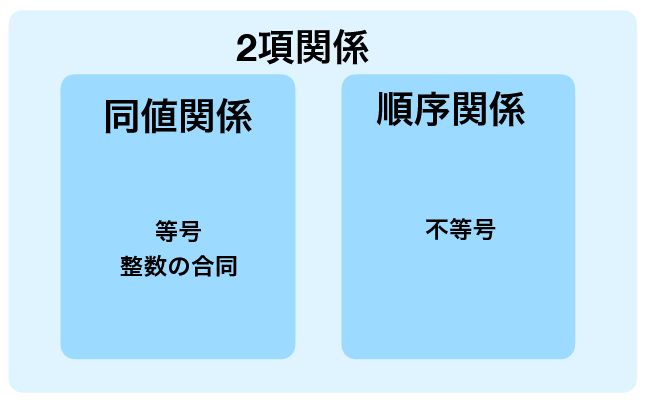
以上、整数の合同を例に、同値関係、2項関係について紹介してきました。
等号や不等号、整数の合同は、すべて2項関係の一種です。等号や整数の合同は同値関係と呼ばれる関係の例。一方で、不等号は同値関係ではなく、順序関係と呼ばれる関係の例です。
同値関係は、商集合や商群の理解に欠かせないので、その基本的な定義をぜひ理解してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
日本評論社 (2008-12-01T00:00:01Z)
¥2,860
Richard Hammack (2019-07-19T00:00:01Z)
¥3,378
こちらもおすすめ