どうも、木村(@kimu3_slime)です。
数学において、商集合は様々なところに登場します。例えば、群論における商群(剰余群)、その応用例である基本群、位相空間論における商空間など。
僕が初めて群論を学び始めたとき、この商群の概念の理解に苦戦しました。剰余類、正規部分群、群を正規部分群で「割る」とは一体何なのだろう、と。集合の直積は、要素の順序対として理解しやすいものでしたが、商集合となると、何が要素となっているのかよくわかりませんでした。
後になって思うのは、商群の理解には、商集合の理解と商集合に付加する群構造の理解の両方が必要だということ。つまり、まず初めに商集合の扱いを知っておくべきだったのです。
そこで今回は、商集合、そして同値関係の概念を、具体例を出しながら扱い、これらを自らの言葉として使えるように紹介します。
目次
商集合の典型例は\(\mathbb{Z}/n\mathbb{Z}\)
「商集合とは何ですか?」と聞かれたときに、最もシンプルで説明しやすいのは加法巡回群\(\mathbb{Z}/n\mathbb{Z}\)です。
解説:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説
\(\mathbb{Z}/n\mathbb{Z}\)はどういう集合であったか。まず\(n=3\)で考えてみましょう。
\(\mathbb{Z}/3\mathbb{Z}\)は、差が3で割り切れる整数を「同一視」してできる集合です。
例えば、\(2,5,8\)を3で割った余りはともに\(2\)です。これらを同一視”\(2=5=8\)”したいわけですが、そのまま等号でつなぐと表記が混乱します。
どういう意味でこれらは等しいのか。それを定義するのが合同算術です。整数\(a,b\)が\(n\)を法として合同であるとは、\(a-b\)が\(n\)で割り切れることと定義し、これを\(a \equiv b \,(\mathrm{mod} \, n)\)と書きます。
すると、さきほどの同一視は\(2\equiv 5\equiv 8\,(\mathrm{mod} \, 3)\)と書けます。
さらに、これを集合的に書き直してみましょう。\(k\in \mathbb{Z}\)に対し、
\[ \begin{aligned}[k]:=\{k+nm \in \mathbb{Z}\mid m\in \mathbb{Z}\}\end{aligned} \]
と集合を定めます。整数\(k\)を基準に、それから\(n\)の整数倍だけ離れた整数を集めた集合です。
\(n=3\)のときならば、\([2]=[5]=[8]\)となるのはすぐわかります。この合同算術によって整数を同一視して得られる集合\([]\)は、3種類しかありません。どのような整数を3で割っても、余りは0か1か2のいずれかだからです。すなわち、
\[ \begin{aligned}\mathbb{Z} / 3\mathbb{Z}:=\{[0],[1],[2]\}\end{aligned} \]
で、一般には
\[ \begin{aligned}\mathbb{Z} / n\mathbb{Z}:=\{[0],[1],\dots,[n-1]\}\end{aligned} \]
となります。
これが商集合の典型例です。商集合の要素は、もとの集合\(\mathbb{Z}\)とは別ものです。すなわち、\([k]\)という集合を要素とする集合なのです。一見して数が表れているので数の集合に見えますが、ここを履き違えないようにしましょう。
(加法巡回群として見れば、通常の数とは異なる「足し算」が働いているので、そういう意味でも普通の整数とは違います)

ポイントは、「合同算術によって等しい」という関係を、集合的な記法\([x]\)(同値類)に書き換えたことです。
さらに、次のように書き換えられます。\(n\mathbb{Z}:=\{nm \in \mathbb{Z}\mid m\in \mathbb{Z}\}\)として、
\[ \begin{aligned}[k]=\{l \in \mathbb{Z}\mid l-k \in n\mathbb{Z}\}\end{aligned} \]
が成立しています。
ここまで来ると、一般に商集合\(X/Y\)をどう定義すれば良いか、予想がついてくるのではないでしょうか。
同値関係、商集合とは何か
さきほどまでは\(\mathbb{Z}\)を考えていましたが、ここからは基準となる集合を\(X\)と一般に表記します。
同値関係の定義
整数の合同関係をより一般化する概念が、同値関係(equivalence relation)です。
合同算術について、当然\(a \equiv a \,(\mathrm{mod} \, n)\)ですし、\(a \equiv b \,(\mathrm{mod} \, n)\)ならば\(b \equiv a \,(\mathrm{mod} \, n)\)で、\(a \equiv b \,(\mathrm{mod} \, n)\)かつ\(b \equiv c \,(\mathrm{mod} \, n)\)ならば\(a \equiv c \,(\mathrm{mod} \, n)\)となっています。
この要請を、同値関係として一般化します。同値関係とは、二項関係\(\sim\)で、次の条件を満たすものです。
(E1)反射律:\(\forall x \in X \quad x\sim x\)
(E2)対称律:\(\forall x,y \in X \quad x\sim y\)ならば\(y \sim x\)
(E3)推移律:\(\forall x,y,z \in X \quad x\sim y,y\sim z\)ならば\(x\sim z\)
ちなみに、二項関係\(\sim\)とは、任意の\(x,y \in X\)に対して\(x\sim y\)または\(\lnot (x\sim y) \)が成立する規則です。合同関係でも、2つの数は合同であるかないかのいずれかでした。関係にあるかないか必ず判別できるのが、二項関係です。
(集合論的に言えば、二項関係は\(X\times X\)の部分集合です。この部分集合に属するかどうかで、二元が関係するかどうかを決められます。)
同値関係は、二項関係でありつつ、対称律や推移律によって、他の要素を同一視して「巻き込んで」いきます。「友達の友達もまた、友達」で、「友達でない人の友達もまた、友達でない」世界です。
さらに、群の場合は、部分群によって定まる同値関係を考えられます。
\(X\)を群で、\(Y\)を\(X\)の部分群とします。
ここで、\(Y\)から同値関係を定めることができます。すなわち、\(x,y\in X\)に対して
\[ \begin{aligned}x\sim y : \Leftrightarrow (y-x \in Y)\end{aligned} \]
とすると、\(\sim \)は同値関係です。反射律は単位元の存在、対称律は逆元の存在、推移律は結合法則に対応しています。
以降でも群の演算を加法的に書いていきますが、次のように乗法的に書いても同じことです。
\[ \begin{aligned}x\sim y : \Leftrightarrow (x^{-1} y\in Y)\end{aligned} \]
巡回群\(\mathbb{Z}/ n\mathbb{Z}\)の場合は、\(X=\mathbb{Z},Y=n\mathbb{Z}\)で、\(Y\)によって定まる同値関係が\(n\)を法とする合同関係なのでした。
同値類・well-defined性
整数の集合に合同関係を入れると、多くの数を同一視してひとつの集合\([k]\)としてまとめることができました。同値関係でも同様のことができます。
\(x\)と同値関係にある要素をすべてまとめてできる、次の集合を\(x\)の同値類(equivalence class)と言います。
\[ \begin{aligned}[x]:=\{y \in X \mid y\sim x \}\end{aligned} \]
文章によっては\([x]\)ではなく、\(C(x),\overline{x}\)で表すこともあります。考えている同値関係を明示的にして、\([x]_{\sim},[x]_{Y}\)と書くのも良いでしょう。いずれにせよ、要素をまとめた集合の立場からものを見る(同値関係によって得られた部分集合に注目する)ので、視点が一段「上」になっていることに注意してください。
同値類を表す元\(x\)を代表元(representative)と呼びます。すべての同値類は、代表元のとり方によらず一意に定まっています(これは同値関係の定義によるものです)。
同値関係を用いた定義において、定義が代表元のとり方によらずに一意に定まっていることを、well-definedであると言います。同値類の定義はwell-definedです。(もしwell-definedでない定義を考えたら、異なる代表元を取ると同じ定義が指し示すはずのものが別物となりえて、議論が矛盾を起こしてしまします。)
\(\mathbb{Z} / 3\mathbb{Z}\)において、\([0]\)を\([3]\)と書こうが\([99]\)と書こうが、それらは同じ集合を指しているので問題ありません。
さきほどのように、\(Y\)を\(X\)の部分群として、そこから定まる同値関係を考えれば、同値類は
\[ \begin{aligned}[x]:=\{y \in X \mid y-x \in Y \}\end{aligned} \]
とも表せます。
(群の言葉では、同値類を剰余類 coset とも呼びます。演算を乗法的に書くとして、\(xY:=\{xy\in X \mid y\in Y\}\)とおくと、\([x]=xY\)です。これを左剰余類と呼びます。同様に右剰余類\(Yx\)が定義されます。
一般の群において演算は可換ではないので、左剰余類と右剰余類を区別しなければなりません。\(X\)が可換群なら左剰余類と右剰余類は一致し、左右の区別なく同値類が定まり、無事に商群 quotient group が定義できます。しかし、\(X\)が非可換群であっても商群は定義できます。すなわち、左剰余類と右剰余類が一致するような部分群\(Y\)を考えれば良いわけです。このとき、\(Y\)を正規部分群 normal subgroup であると言います。\(n\mathbb{Z}\)は\(\mathbb{Z}\)の正規部分群です。)
このように同値類を定義すると、集合\(X\)は同値類\([x]\)たちによってクラス分けされます。
つまり、任意の要素\(x\in X\)はいずれかの同値類に属していて、かつ、異なる同値類には共通部分がありません。
\[ \begin{aligned}X = \bigcup \{[x] \in 2^X \mid x\in X\}\end{aligned} \]
\[ \begin{aligned}[x]\neq [y] \Rightarrow [x]\cap [y] = \emptyset\end{aligned} \]
\(X\)のどの要素もいずれかの同値類に属していて、かつその分類は混じり合うことがないようになっているのです。
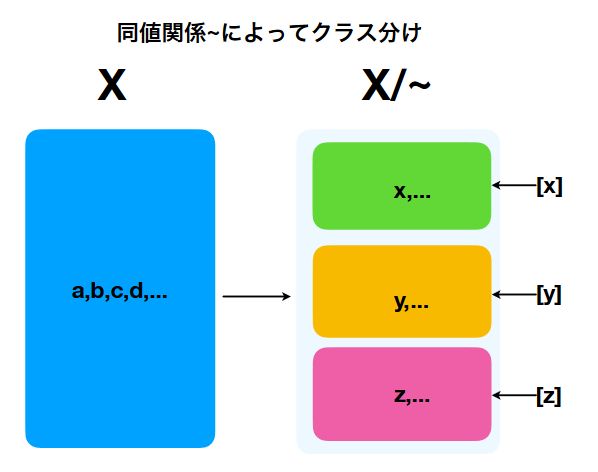
図では有限個の同値類に類別されていますが、一般に同値類は非可算無限となります。以降で紹介するトーラス、射影直線では、同値類は実無限の分だけあります。
参考:無限集合の多さ(濃度)はどのくらい? 可算無限、カントールの対角線論法とは
商集合
同値関係、同値類の概念を定義すれば、商集合(quotient set)が定義できます。つまり、それは同値類全体の集合です。
\[ \begin{aligned}X/\sim := \{[x] \in 2^X \mid x\in X\}\end{aligned} \]
部分群\(Y\)によって定まる同値関係を考えたときも、同様に
\[ \begin{aligned}X/Y := \{[x] \in 2^X \mid x\in X\}\end{aligned} \]
と書きます。ここで、\(2^X\)は\(X\)の部分集合全体で、\([x] \in 2^X\)は\([x]\subset X\)を意味します。
これでようやく、\(\mathbb{Z}/ n\mathbb{Z}\)という表記が妥当なことがわかりました。
(\(X\)を\(*\)を演算とする群、\(Y\)をその正規部分群とします。そして、商集合\(X/Y\)の演算を\([x]*[y]:=[x*y]\)と定めると、これはwell-definedです。こうして定まる群\(X/Y\)を商群 quotient group と言います。)
僕が学び初めのときにつまづいたのは、商集合とはどういう集合なのか、ということです。つまり、\(X/Y\)から要素を取り出すと、それは何なのかと。
商集合の要素は、同値類\([x]\)です。つまり、\(X\)の部分集合を要素としています。部分集合を要素とする集合というのは、例えば\(\{\{a\},\{a,b\} \}\)です。集合論を学び初めのときは、集合を要素とする集合の意味、\(\{a\}\)と\(\{\{a\} \}\)の違いがわかっていませんでした。\(\{a\} \in \{\{a\} \}\)であり、\(\{a\} \subset \{\{a\} \}\)ではないのです。
位相空間の定義でも、\(X\)の部分集合の集まり(=\(2^X\)の部分集合)を考え、それを開集合系と呼びます。\(X\)と、\(X\)の(部分)集合を要素とする集合の違いは理解できるようになっておきましょう。
商集合の要素は同値類\([x]\)で、同値類とは何かが定義に遡って言えるようになれば、商集合は理解できるでしょう。最初のうちは、\(\mathbb{Z}/n\mathbb{Z}\)を例として思い浮かべると、一般の商集合も扱いやすいと思います。
商写像・自然な射影・標準的な写像
商集合\(X/Y\)が決まると、もとの集合\(X\)から商集合\(X/Y\)へ自然と定まる写像が存在します。つまり、もとの要素をその同値類へ対応させる写像
\[ \begin{aligned}p:X\to X/Y, x\mapsto[x]\end{aligned} \]
が存在します。これを商写像(quotient map)、自然な射影(natural projection)、標準的な写像(canonical map)と呼びます。その定義から、当然全射です。
(\(Y\)を\(X\)の正規部分群とするとき、自然な射影は全射な準同型写像で、\(\mathrm{Ker}\,p =Y\)です。これは準同型定理を支える事実となっています。)
同値関係・商空間が与えられる前に、逆に、(全射な)写像\(f:X\to Z\)から出発して考えます。
このとき、\(X\)の元に対して、
\[ \begin{aligned}x\sim y :\Leftrightarrow f(x)=f(y)\end{aligned} \]
と定めると、関係\(\sim\)は同値関係となります。(これを写像\(f\)に付随する同値関係という)
こうして商集合\(X/\sim\)を定義できます。また、\(X/\sim\)と\(Z\)の間には全単射が存在します。
(位相空間における商空間・商位相は、むしろこちらの商写像によって定義されることがあります。)
トーラス \(\mathbb{R}/\mathbb{Z}\)
ここからの話は商集合の例を挙げるにとどめ、細部(付随する構造、証明)には立ち入りません。
実数の集合\(\mathbb{R}\)において整数\(\mathbb{Z}\)だけ離れた点を同一視して得られる商集合\(\mathbb{R}/\mathbb{Z}\)を考えましょう。
つまり、\(x \sim y\)を\(x-y \in \mathbb{Z}\)なる同値関係として捉えます。
無限に続く直線のうち、整数1だけ離れた点を同一視する。例えば、\(0,1,2\)が同じ点(同値類)となります。直線をばねのように曲げて円環状に重ね合わせたものと見れます。
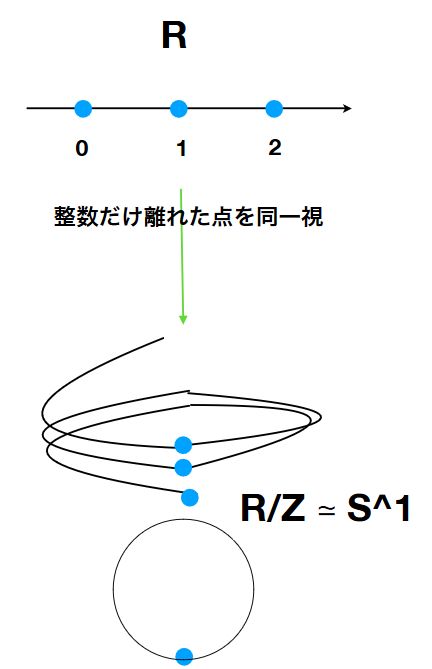
じつは\(\mathbb{R}/\mathbb{Z}\)は、円周\(S^1:=\{(x,y)\in \mathbb{R}^2 \mid x^2+y^2=1\}\)と一対一に対応します。
(\(g:\mathbb{R}/\mathbb{Z}\to S^1, g([x]):= (\cos(2\pi x),\sin (2\pi x))\)がきちんと定義される。さらには、位相同型で、群としても同型:位相群として同型になる。群準同型定理の応用例とも言える。)
(自然な射影 \(\mathbb{R}\to \mathbb{R}/\mathbb{Z} \simeq S^1\) は、\(\mathbb{R}\)を使って\(S^1\)を無限に覆っているように見えます。位相幾何学において、この射影は被覆写像、\(\mathbb{R}\)は被覆空間、\(S^1\)は底空間と呼ばれます。)
より一般に、\(\mathbb{T}^N := S^1 \times \cdots S^1\)を\(N\)次元トーラスと言います。円周\(S^1\)は1次元のトーラスで、2次元トーラスはドーナツのような図形です。
(1次元トーラスは、複素単位円周、1次のユニタリ群\(U(1)\)、2次の特殊直交群\(SO(2)\)とも位相群として同型になります。つまり、\(\mathbb{R}/\mathbb{Z}\)は一次元的な回転を表しているとも言えるのです。また、トーラスは群構造と多様体の構造を併せ持つ、リー群の例でもあります。)
射影空間 \(\mathbb{RP}\)
平面から原点だけ除いた集合\(\mathbb{R}^2 \backslash \{0\} \)において、原点を通る同一の直線上にある点を同一視しましょう。
つまり、\((x_1,x_2) \sim (y_1, y_2)\)を\(\exists\, t\neq0 \quad x_1=t y_1,x_2 = t y_2\)となる同値関係として考えます。そして、\((x_1,x_2)\)の同値類を\([x_1:x_2]\)と書きます。
このとき、\(\mathbb{RP}:=(\mathbb{R}^2 \backslash \{0\})/ \sim \)を射影直線(projective line)、または射影空間(projective space)と呼びます。
その要素(同値類)は、平面上の原点を通る直線であることが思い浮かべられるでしょうか。射影空間の「点」は、こうした直線たちです。
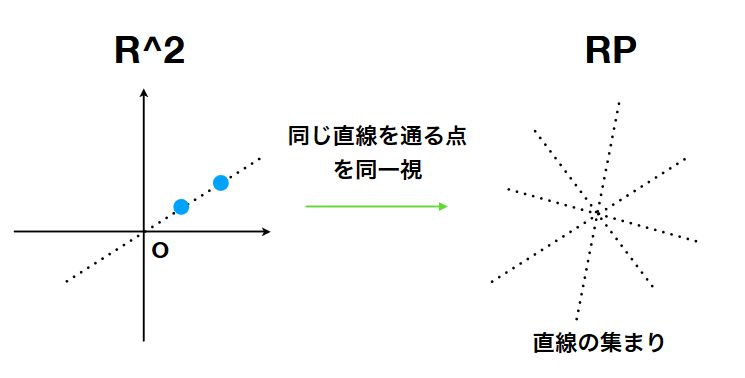
射影直線は、円周\(S^1\)上の各点\(x\)につき、\(x\)と\(-x\)を同一視したものとしても見ることができます。原点につき正反対の位置にある点は、対蹠点(antipodal point)と呼ばれるものです。
より一般には、同様の同値関係を考えて、\(\mathbb{RP}^N:=(\mathbb{R}^{N+1} \backslash \{0\})/ \sim \)は\(N\)次元射影空間と呼ばれます。係数を複素数にすれば、複素射影空間です。(射影空間には、多様体としての構造が入ります)
まとめ
巡回群\(\mathbb{Z}/n\mathbb{Z}\)と整数の合同関係を典型例として、同値関係、同値類、商集合の定義を紹介しました。そしてその例として、トーラスと射影空間を見てきました。
商集合の理解のポイントは、同値類の理解です。同値類が同値関係や部分集合・部分群・写像から入るケースがあります。これらを自由に行き来できれば、商集合だけでなく、商群や商空間も理解しやすくなることでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
無限集合の多さ(濃度)はどのくらい? 可算無限、カントールの対角線論法とは