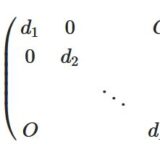複素数と行列の対応関係：行列表現

どうも、木村（@kimu3_slime）です。

今回はそれに限らず、複素数そのものはある種の行列と対応関係にあることを紹介します。

複素数の積と回転行列
複素数と行列の対応関係
- 一対一の対応
- 和と積を保つこと
こちらもおすすめ

複素数の積と回転行列

複素平面上において、\(z=1\)は実軸上にあります。これに\(i\)をかけると、虚軸に写ります。さらに\(i\)をかけると、\(i^2 =-1\)と実軸に戻ってきます。

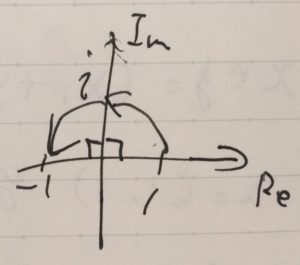
これは\(R_{\frac{\pi}{2}}= \begin{pmatrix} 0& -1\\ 1 & 0 \end{pmatrix}\)という90度の回転行列に対応したものです。

一般に、大きさ\(1\)の複素数は、何らかの回転行列に対応しています。

\[ \begin{aligned}R_\theta = \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix} \leftrightarrow e^{i\theta}\end{aligned} \]

詳しくは：複素数の積＝回転行列の積：対応関係を解説、回転行列とは？導出と例、性質を紹介

複素数と行列の対応関係

大きさが\(1\)とは限らない複素数に対しても、何らかの行列と関連づけることができます。それを紹介していきましょう。

\(z= x+ yi\)と実部虚部を表すとき、成分が実数である正方行列

\[ \begin{aligned}C(z) = \begin{pmatrix} x & y\\ -y & x \end{pmatrix}\end{aligned} \]

との対応関係を考えていきましょう。

例えば\(z=1\)のときは、\(C(z) =I\)と単位行列に対応しています。

\(x^2 +y ^2=1\)のときは、大きさが\(|z|=x^2+y^2=1\)で、回転行列に対応するケースです。今回はそれに限らない一般の場合で考えていきます。

一対一の対応

\(z\)がどんな複素数であっても、実部と虚部を使って\( \begin{pmatrix} x & y\\ -y & x \end{pmatrix}\)という形の行列が生み出せます。この対応関係は、一対一のものとなります。

まず、行列の表し方に対して、複素数はただひとつ対応します。\(C(z)=C(w)\)ならば、\(z=w\)が成り立ちます。

仮に複素数\(z= x_1+y_1 i\)、\(w = x_2+ y_2 i\)によって、\(C(z)=\begin{pmatrix} x_1 & y_1\\ -y_1 & x_1 \end{pmatrix} = \begin{pmatrix} x_2 & y_2\\ -y_2 & x_2 \end{pmatrix}=C(w)\)となったとしましょう。行列の成分を比較すれば、\(x_1 =x_2,y_1 =y_2\)となり、\(z=w\)となります（単射性）。

逆に、この形のどんな行列\( \begin{pmatrix} x & y\\ -y & x \end{pmatrix}\)に対しても、その成分を使って\(z = x+iy\)という複素数を定めることができます（全射性）。

つまり、\(z \in \mathbb{C}\)と特殊な行列\(\begin{pmatrix} x & y\\ -y & x \end{pmatrix}\)は一対一（全単射）の対応関係にあるわけです。

参考：写像の単射・全射・全単射の判定、証明の書き方

和と積を保つこと

このように要素が対応するだけでなく、複素数の足し算と掛け算（和と積）についても、この行列は対応しているのです。

まず、\(C(z)+C(w) = C(z+w)\)となります。確かめましょう。

複素数の和は、\(z+w= (x_1 +y_1 i)+(x_2 +y_2i)\\=(x_1+x_2)+(y_1 +y_2)i\)でした。

\[ \begin{aligned} C(z)+C(w) &=\begin{pmatrix} x_1 & y_1\\ -y_1 & x_1 \end{pmatrix} + \begin{pmatrix} x_2 & y_2\\ -y_2 & x_2 \end{pmatrix} \\ &= \begin{pmatrix} x_1+x_2 & y_1+y_2\\ -(y_1+y_2) & x_1 +x_2\end{pmatrix} \\ &=C(z+w)\end{aligned} \]

と成り立っています。

続いて、\(C(zw)=C(z)C(w)\)となります。

複素数の積は、\(zw= (x_1 +y_1 i)(x_2 +y_2i)\\=(x_1x_2 -y_1y_2)+(x_1 y_2+y_1 x_2)i\)でした。

\[ \begin{aligned} C(zw) &=\begin{pmatrix}x_1x_2 -y_1y_2 & x_1 y_2+y_1 x_2\\ -(x_1 y_2+y_1 x_2) & x_1x_2 -y_1y_2 \end{pmatrix} \end{aligned} \]

であり、行列の積を計算すれば

\[ \begin{aligned} C(z)C(w) &= \begin{pmatrix} x_1 & y_1\\ -y_1 & x_1 \end{pmatrix} \begin{pmatrix} x_2 & y_2\\ -y_2 & x_2 \end{pmatrix}\\ &=\begin{pmatrix}x_1x_2 -y_1y_2 & x_1 y_2+y_1 x_2\\ -(x_1 y_2+y_1 x_2) & x_1x_2 -y_1y_2 \end{pmatrix} \end{aligned} \]

なので、両者が一致することがわかりました。

ここから、複素数の逆数\(\frac{1}{z}\)に対応した行列\(C(\frac{1}{z})\)が、\(C(z)\)の逆行列となること\(C(z) ^{-1} =C(\frac{1}{z})\)もわかります。

\(z \neq 0\)としましょう。\(C(\frac{1}{z})\)が\(C(z)\)の逆行列となることを示します。

積の法則\(C(zw) =C(z)C(w)\)において、\(w= \frac{1}{z}\)とすれば、\(C(1)= C(z)C(\frac{1}{z})\)です。左辺は単位行列\(C(1) =I\)なので、\(C(z) ^{-1} =C(\frac{1}{z})\)が示されました。

\(C(z)\)の行列式は\(\det C(z) = x^2+y^2\)です。複素数について\(z\neq 0\)とは、実部も虚部も0でない、すなわち\(x \neq 0 \)かつ\(y \neq 0\)のことでした。これは\(x^2 +y ^2 \neq 0\)、行列式が0でないことに対応していますね。

参考：可逆な行列（正則行列）とは？例と同値な条件

以上によって、

\[ \begin{aligned}z =x+iy \leftrightarrow \begin{pmatrix} x & y\\ -y & x \end{pmatrix}\end{aligned} \]

という対応関係は、複素数の和や積を、行列の和と積にうまく写していることがわかりました。

集合や代数の言葉を使うと、もう少し言い換えることができます。

\(\mathbb{C }\)を複素数のなす集合、\(M(2,2;\mathbb{R})\)をサイズ\(2,2\)の実成分の行列がなす集合とします。今回考えたのは、\(M_C :=\{ \begin{pmatrix} x & y\\ -y & x \end{pmatrix} \in M(2,2;\mathbb{R})\}\)という形の行列でした。

対応関係は、\(C : \mathbb{C }\to M_C\)という写像と考えられます。この写像は全単射であり、和と積を保存する写像であることを今回確かめました。

要素を一対一に対応させてかつ演算を保存する写像は、一般に同型写像と呼ばれます。和と積が考えられる集合は体と呼ばれますが、今回示したのは\(C\)が体としての同型写像であることというわけです。

参考：群論入門～回転群と巡回群を例に、群の定義・同型・位数を解説

（今回は複素数を行列で表現しましたが、「何かを行列で表現する」という手法は普遍的です。線形代数学では、線形写像を行列で表現すること：表現行列について学びます。このように、演算の性質を知りたい要素をうまく行列として表現できないか、と考える分野は、抽象代数学において表現論と呼ばれています。）

以上、複素数と行列の対応関係を紹介してきました。

今回は複素数というものが存在するという立場から議論しました。しかし、実数と行列の計算しか論理的に知らないという立場からも、行列\( \begin{pmatrix} x & y\\ -y & x \end{pmatrix}\)を使って「複素数」なるものを構成できるわけです。

つまり、行列の計算は複素数の定義に使えます。さらに、複素数を拡張したような四元数についても、今回のようにある種の（複素）行列を対応させられます。

なぜ行列の積をこんな風に定義するのか、という理由のひとつとしても、今回の対応関係を思い出してみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。