どうも、木村(@kimu3_slime)です。
平面上の幾何学において、一方の図形を回転させてもう一方の図形に重なるとき、それらは合同であると呼ばれます。点や図形を回転させるという操作は、線形代数では行列を使って表せるのです。
今回は、回転行列の導出と例、その性質を紹介していきます。
回転行列とは
平面\(\mathbb{R}^2\)における回転行列を導出してみましょう。
平面上の点を、原点\((0,0)\)を中心に角度\(\theta\)だけ回転させます。特に、\((1,0),(0,1)\)がどこに写るか調べてみましょう。
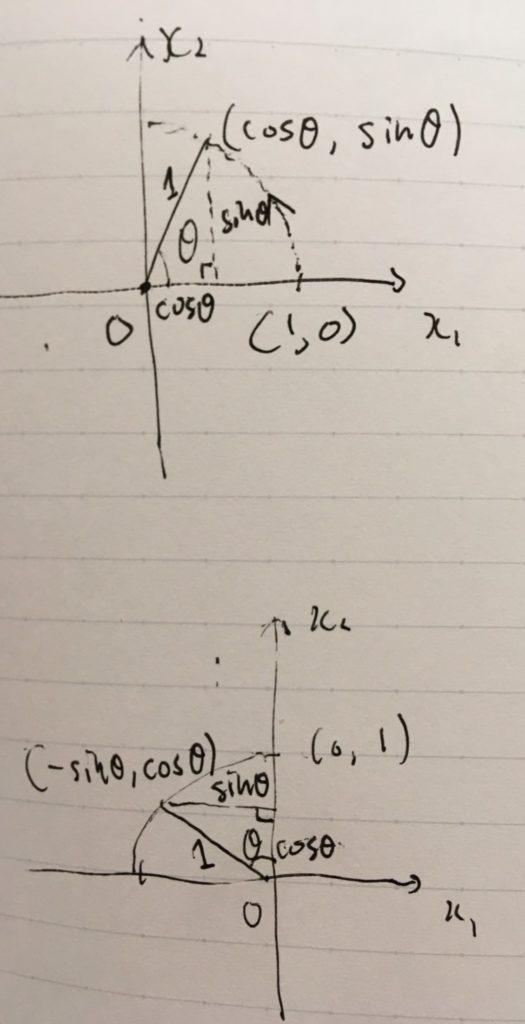
三角関数の定義より、上の図のようになります。\((1,0)\)は回転によって\((\cos \theta, \sin \theta)\)へ、\((0,1)\)は\((-\sin\theta , \cos \theta)\)へ写ります。鋭角の場合で図示していましたが、一般角の場合も同様です(そうなるように三角関数は定義されている)。
回転行列を\(R_\theta=\begin{pmatrix} a& b\\c & d \end{pmatrix} \)とすれば、
\[ \begin{aligned}\begin{pmatrix} a& b\\c & d \end{pmatrix} \begin{pmatrix} 1\\0 \end{pmatrix}= \begin{pmatrix} \cos \theta\\ \sin \theta \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} a& b\\c & d \end{pmatrix} \begin{pmatrix} 0\\1 \end{pmatrix}= \begin{pmatrix} -\sin \theta\\ \cos \theta \end{pmatrix}\end{aligned} \]
です。
よって、\(R_\theta = \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix}\)が回転行列です。この形は覚えてしまって良いと思いますが、忘れたら今回のように図を書いて確認できます。
回転行列の例
\(\theta =0\)のとき、\(R_\theta = \begin{pmatrix} \cos 0& -\sin 0\\ \sin0 & \cos 0\end{pmatrix}=I\)で単位行列です。何も回転させないということですね。\(\theta = 2 n\pi ,n \in \mathbb{Z}\)のときも、三角関数の周期性から、単位行列です。
\(\theta =\pi \)のとき、\(R_\pi = \begin{pmatrix} \cos \pi& -\sin \pi\\ \sin \pi & \cos \pi\end{pmatrix}=-I\)です。つまり、180度回転させることは、ベクトルを逆向きに変えるのと同じ。
回転行列は、コンピュータにおける画像処理でそのまま使われています。


参考:線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
\( \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\)は、\(\theta =\frac{\pi}{2}\)、90度の回転行列です。\( \begin{pmatrix} a & -b \\ b & a \end{pmatrix}\)の形の行列を、回転行列と見抜けるのは大事。
可換ではない行列\(AB \neq BA\)の例は、ここから簡単に作れます。\(R_{\frac{\pi}{2}}\)と、(\(x_1\)軸に関する)反転行列\(\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\)は可換ではありません。反転させてから回転と、回転させてから反転は等しくありません。行列計算で確かめてみてください。
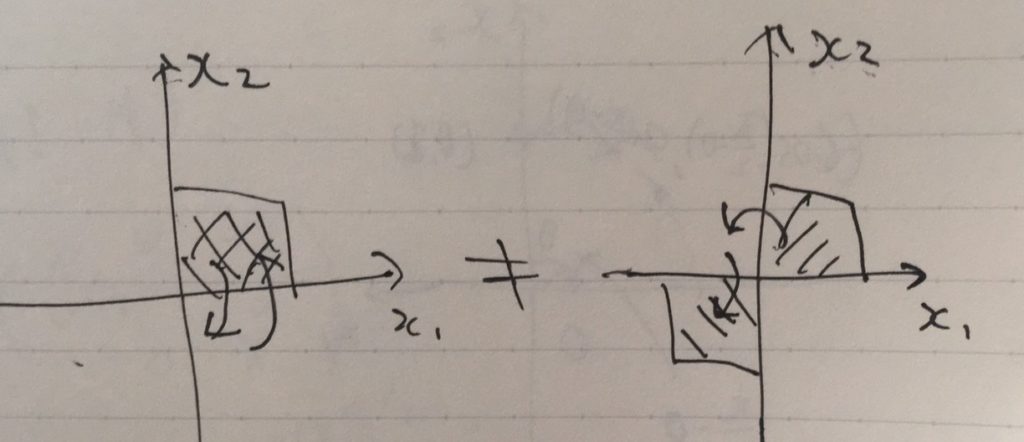
回転と反転を合わせた操作は、二面体群として抽象化されています。「行列の積に順序があるってどういうことなの?」と思う人は、このイメージをつかみましょう。
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説、図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説
回転行列の性質
回転行列の性質を簡単に紹介しましょう。
回転行列の積は、回転の足し合わせ
\(R_{\beta}R_{\alpha}=R_{\alpha +\beta}\)
角度\(\alpha\)回転させてからさらに\(\beta\)回転させる操作は、\(\alpha+\beta\)回転させることと同じ。当たり前のようですが、きちんと式の上でも成り立っています。
\[\begin{aligned} R_{\beta}R_{\alpha} &=\begin{pmatrix} \cos \beta& -\sin \beta\\ \sin\beta & \cos\beta \end{pmatrix} \begin{pmatrix} \cos \alpha& -\sin \alpha\\ \sin\alpha & \cos\alpha \end{pmatrix} \\ &=\begin{pmatrix} \cos \alpha \cos \beta -\sin\alpha \sin \beta& -(\sin \alpha \cos \beta +\cos \alpha \sin \beta)\\ \sin \alpha \cos \beta +\cos \alpha \sin \beta & \cos \alpha \cos \beta -\sin\alpha \sin \beta \end{pmatrix} \\ &= \begin{pmatrix} \cos (\alpha +\beta)& -\sin (\alpha +\beta)\\ \sin(\alpha +\beta) & \cos (\alpha +\beta)\end{pmatrix}\\ &= R_{\alpha +\beta} \end{aligned} \]
途中の式変形は、三角関数の加法定理です。
逆に言えば、回転行列の定義と行列の積を覚えていれば、この計算から加法定理を導けるとも言えます。もし加法定理を忘れてしまったら、この手順を試すのも良いでしょう。
行列式は1で、等長変換
\(\det R_{\theta}=1\)
行列式の定義より\(\det R_{\theta}=\cos ^2 \theta+ \sin ^2 \theta\)なので、三角関数の性質より1に等しいです。
角度\(\theta\)が何であろうが、回転行列であれば行列式が1となることに注意しましょう。
特に、回転行列はベクトルの「長さを保存」します。
\[ \begin{aligned} \|R_{\theta } x\|& =\sqrt{(x_1\cos \theta-x_2\sin \theta)^ 2+(x_1 \sin \theta +x_2 \cos \beta)^2} \\& = \sqrt{x_1 ^2 (\cos^2 \theta + \sin ^2 \theta)+x_2 ^2 (\sin^2 \theta +\cos ^2 \theta)} \\& =\| x\| \end{aligned} \]
(\(\|x\|\)はベクトルのユークリッドノルム=大きさ。別記事で紹介予定)
一般に、\(X,Y\)をノルム空間として、写像\(f:X\to Y\)が\(\|x-y\|_X = \|f(x)-f(y)\|_Y\)を満たす時、\(f\)は等長写像(isometry)と呼ばれます。\(X=Y\)のときは等長変換とも。
回転行列は等長変換です。
平面幾何学において、線形変換+平行移動で表される変換(アフィン変換)であり、等長写像であるものは、合同変換とも呼ばれます。合同な図形の幾何学には、距離を保つ写像が関わっているわけですね。
逆行列が転置行列となる:回転行列は直交行列
回転行列の行列式は0ではないので、回転行列は可逆です。つまり逆行列が存在します。
\((R_\theta) ^{-1}= (R_\theta) ^{\top} = R_{-\theta}\)
ここで\((R_\theta )^{\top}\)は\(R_\theta\)の転置行列です。一般に行列\(A=(a_{ij})\)の転置行列は、\(A^{\top}=(a_{ji})\)と行と列を入れ替えた、対角成分について折り返した行列と定義されます。
角度\(\theta\)の回転の逆行列は、角度\(-\theta \)の回転である。これも当たり前のようですが、確かめてみましょう。
三角関数の性質より、
\[\begin{aligned} (R_\theta) ^{\top} &=\begin{pmatrix} \cos \theta& \sin \theta\\ -\sin\theta & \cos\theta \end{pmatrix} \\ &=\begin{pmatrix} \cos (-\theta)& -\sin(-\theta)\\ \sin(-\theta) & \cos(-\theta) \end{pmatrix} \\ &= R_{-\theta} \end{aligned} \]
です。
よって、回転行列の積の性質を用いれば、\(R_{-\theta}R_\theta =R_{-\theta +\theta}=R_0 =I\)。これは逆行列の定義なので、\((R_\theta) ^{-1}=R_{-\theta}\)が示せました。
一般に、逆行列が転置行列になる \(X^{-1}=X^{\top}\) 行列\(X\)を直交行列(orthogonal matrix)と言います。回転行列は直交行列です。
直交行列の行ベクトル(列ベクトル)は、直交していて、その大きさが1です。また、直交行列の行列式は1か-1になることが知られています。
回転行列はすべて直交行列ですが、すべての直交行列が回転行列であるわけではありません。例えばある種の置換行列\(\begin{pmatrix}0&1 \\ 1 & 0 \end{pmatrix}\)は、直交行列ではありますが回転行列ではありません。

回転行列全体の集合は、回転群、特殊直交群\(SO\)とも呼ばれます。今回は2次元の回転行列を紹介しましたが、一般には、直交行列であり、かつ\(\det A=1\)となる行列を回転行列と呼びます。
例えば、\( \begin{pmatrix} \cos \theta& -\sin \theta&0\\ \sin\theta & \cos \theta&0 \\ 0& 0& 1 \end{pmatrix}\)は、\(x_3\)を軸とする\(x_1-x_2\)平面の回転です。
また、平面上の回転は、複素数の積との対応関係があります。複素数平面の話は、別記事で紹介予定。
今回は、回転行列の導出と例、その性質を紹介してきました。\(2\times 2\)と小さいサイズの行列でありながら、線形変換というものを理解するのに良い題材だと思います。ぜひ回転行列に親しんでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥8,800
東京大学出版会 (1966-03-31T00:00:01Z)
¥2,090
こちらもおすすめ
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説