どうも、木村(@kimu3_slime)です。
今回は、図形の対称性を記述する二面体群、多面体群、その応用例として点群・結晶群を簡単に紹介したいと思います。
前提知識:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説
二面体群
二面体群(Dihedral group)\(D_n\)とは、平面\(\mathbb{R}^2\)における正多角形(正\(n\)角形)の対称性を記述する群です。
どう記述するかというと、正多角形をそれ自身に移すような変換の集まりを考えるのです。その変換とは、回転と鏡映です。
(平行移動、回転、鏡映をあわせて、合同変換・運動と呼び、それらがなす群を合同変換群・運動群と呼びます。合同変換は点の間の距離を変えない性質を持つ、等長変換です。エルランゲン・プログラムによると、平面幾何、すなわちユークリッド幾何は、合同変換によって変わらない性質を扱う分野です。
二面体群は、合同変換のうち平行移動を考えないもので、合同変換群の部分群となっています。)
変換と言われてもピンとこないと思うので、正三角形的な対称性\(D_3\)について、具体的に見ていきましょう。正三角形の頂点を\(a,b,c\)とします。
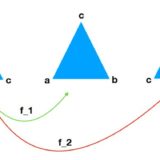
正三角形の回転は、頂点を次の画像のように順に入れ替える操作、すなわち置換\(f_1,f_2\)として表されます。
\(f=f_1\)とすると、\(f_2=f^2\)で、\(e=f^3\)(\(e\)は恒等置換、何もしないという回転を表す)です。このループする回転変換の集まりは、巡回群\(C_3\)と呼ばれるのでした。
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説
正三角形をそれ自身に移す変換は、回転だけではありません。正三角形は、ひっくり返しても三角形です。
次の画像のように、頂点\(a,b,c\)を通る軸(直線)\(\ell_a,\ell_b,\ell_c\)を定めます。そして、その軸に関する鏡映(反転)を、それぞれ\(r_1,r_2,r_3\)とします。
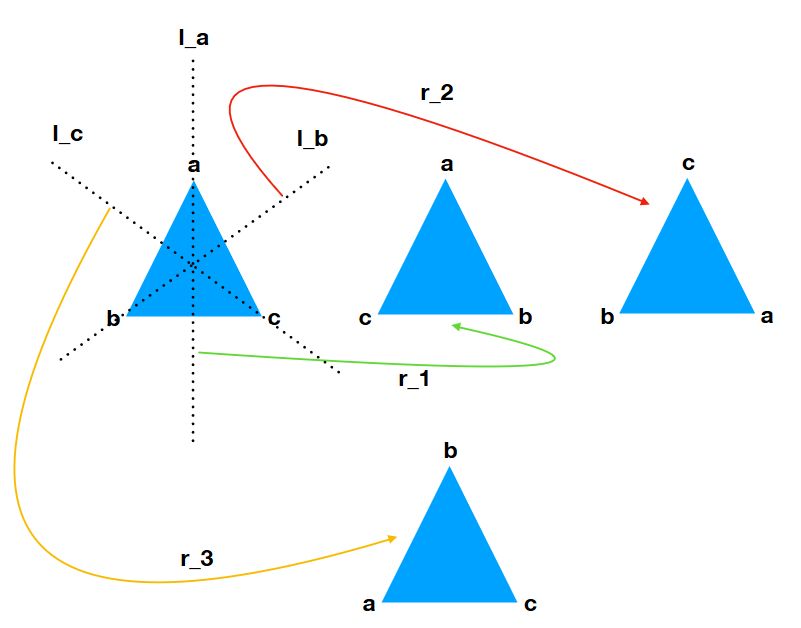
鏡映も、頂点の入れ替え操作、すなわち置換の一種です。\(r_1\)は、\(a\)を入れ替えず、\(b,c\)を入れ替える置換\((a,c,b)\)です。\(r_2,r_3\)も、同様に理解できます。2つの要素のみを入れ替え、他を入れ替えないような置換を互換(transposition)と呼びます。
どの鏡映も、二回行えばもとに戻りますね。すなわち、\(r_1^2=r_2^2=r_3^2=e\)です。
これで三角形の合同変換を表し尽くしました。回転変換、鏡映変換を組み合わせた集まり
\[ \begin{aligned}D_3:=\{e,f,f^2,r_1,r_2,r_3\}\end{aligned} \]
を\(3\)次の二面体群と呼びます。正三角形的な対称性は、\(D_3\)として表されるわけです。
二面体群は、(\(n\ge3\)のとき)非可換群です。例えば、\(r_1 \circ f=(c,b,a)=r_2\)ですが、\(f\circ r_1=(b,a,c)=r_3\)なので。表裏をひっくり返すと、同じ回転は逆方向の別物になります。
二面体群\(D_3\)の要素間の関係を表すケーリーグラフは次のようになります。青矢印が回転\(f\)、赤矢印が鏡映\(r_1\)に対応しています。
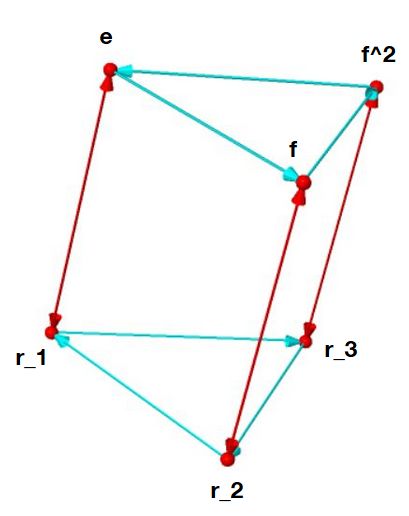
逆回転\(f^{-1}=f^2\)は、鏡の中での順回転\(r_1 f r_1\)に対応している\(f^{-1}=r_1 f r_1\)ことがわかりますね。
正三角形では、3回の回転と3軸の反転がありました。正四角形(正方形)ならば、4回の回転と4軸に関する鏡映によって移り合います。
より一般に、正\(n\)角形をそれ自身に移す回転変換、鏡映変換の集まりを\(n\)次の二面体群\(D_n\)と呼びます。

二面体群は、行列を通して表現できます。
\[ \begin{aligned}f_k=\begin{pmatrix} \cos (\frac{2\pi k}{n}) & -\sin (\frac{2\pi k}{n}) \\ \sin (\frac{2\pi k}{n}) & \cos (\frac{2\pi k}{n}) \end{pmatrix} \end{aligned} \]
\[ \begin{aligned}r_k=\begin{pmatrix} \cos (\frac{2\pi k}{n}) & \sin (\frac{2\pi k}{n}) \\ \sin (\frac{2\pi k}{n}) & – \cos (\frac{2\pi k}{n}) \end{pmatrix} \end{aligned} \]
とすると、\(f_k\)は原点中心で反時計回りに\(\frac{2\pi k}{n}\)の回転を表す行列、\(r_k\)は\(x\)軸と\(\frac{2\pi k}{n}\)の角度をなす直線\(\ell_k\)に関する鏡映です(\(0\leq k \leq n-1\))。
\[ \begin{aligned}r_k=f_k \begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix} \end{aligned} \]
という関係があるように、特定の直線に関する鏡映は、回転と反射の組み合わせなのです。
\(D_3\)では、\(f^2 =e,r^2=e,f^{-1} = rfr\)という関係が成り立っていました。一般の二面体群も、この関係を満たす\(f,r\)により生成される群
\[ \begin{aligned}D_n= \langle f,r \mid f^n =e,r^2=e,f^{-1} = rfr \rangle\end{aligned} \]
としても定義できます。\(f^n =e\)は回転が巡回的であること、\(r^2=e\)は2回鏡映が自身に戻ってくること、\(f^{-1} = rfr\)は逆回転とは鏡映での順回転であること、です。
ここまで来れば、二面体群の要素間の計算と、それが表す変換もイメージできるようになってきているのではないでしょうか。
多面体群
二面体群については詳しく紹介しましたが、ここからはざっくりとした話として進めます。(細部に立ち入ると長いので)
多面体群(polyhedral group)は、その名の通り、3次元空間における正多面体の対称性を記述する群です。二面体群と同様、正多面体をそれ自身へ重ねる変換のなす群として定義されます。
今までに見てきた二面体群は、平面における正多角形を表裏二面の薄い立体としてみなしたもので、多面体群の特殊ケースでした。
正多面体は、正4面体、正6面体(立方体)、正8面体、正12面体、正20面体と、限られたパターン(5種類)しかありません。これらは、プラトン立体(Platonic solid)とも呼ばれます。

この図は、計算ソフトSageMathを使った次のコードによって作成しました。各正多面体の関数名は「Common Graphs」のPlatonic solidsを参照。
1 2 | G=graphs.DodecahedralGraph() G.show3d() |
正多面体群は、次のような記号で表されます。
\(T\) 正4面体群。Tetrahedronの頭文字から。位数12で、\(A_4\)と同型。
\(O\) 正8面体群=正6面体群。Octahedronの頭文字から。位数24で、\(S_4\)と同型。
\(I\) 正20面体群=正12面体群。Icosahedronの頭文字から。位数60で、\(A_5\)と同型。
正四面体群を簡単に見てみましょう。
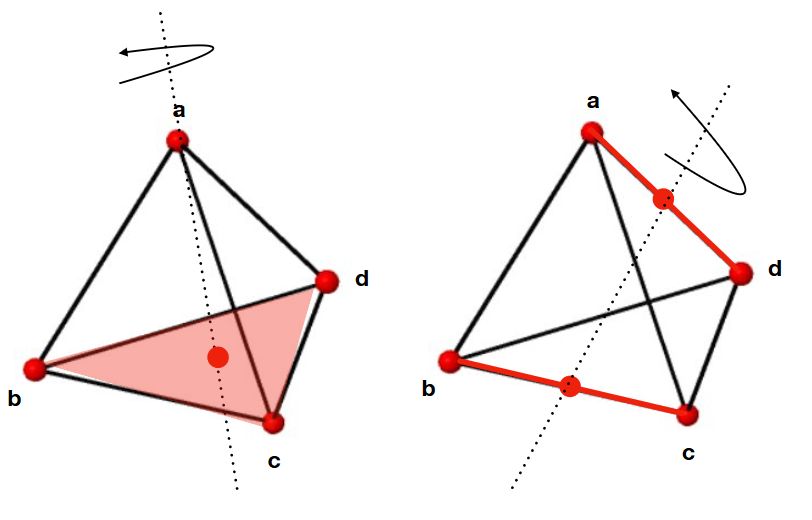
まず、ある頂点とその反対側の面を中心とする軸に関する\(60^{\circ}\)回転で、2つの要素があります(3回対称軸)。この軸は4つあるので、2*4=8つの要素です。
また、ある辺とその反対側の辺、それぞれの中点を通る軸に関しては、\(180^{\circ}\)回転で重なり合うので、1つの要素があります(2回対称軸)。上の図で言えば、\(a\)が\(d\)に、\(b\)が\(c\)に入れ替わります。こうした軸は3つあるので、1*3=3つの要素があります。
ここに恒等置換を加えれば、回転を表すのは12個の要素です。これが正四面体群\(T\)です。省略しますが、同様にして8面体群\(O\)、20面体群\(I\)が考えられます。
正多面群については、「群論の味わい」や「Polyhedral group – Wikipedia」も参照してみてください。
点群・結晶群
二面体群や多面体群は、化学物質や結晶構造の分類に応用されています。それが点群・結晶群です。
点群(point group)は、ある1点を動かさないような変換のなす群の総称です。
分子の対称性は、シェーンフリース記号(Schönflies notation)と呼ばれる記法によって表されます。その記号は、これまでに見てきた\(C_n,D_n,T,O,I\)(など。主記号という)に合わせ、鏡映面がある場合は\(h,v,d\)などの記号(付加記号)が添字に加えられます。(\(S_n\)という記号も用いられますが、対称群とは異なる意味で使われるので注意)
例えば、アンモニア\(\mathrm{NH_3}\)は3回の平面回転\(C_3\)で、回転軸を通る面に関して鏡映対称(垂直)なので、\(C_{3v}\)と表されます。ヘモグロビンのような高分子でもシェーンフリース記法は利用されているようです。
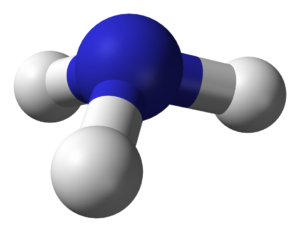
画像引用:Ammonia-3D-balls-A.png, – Wikipedia
参考:点群記号の規則 – 分子分光学、2. 点群について – 生物学的集合体と対称性
結晶群、または空間群(space group)は、3次元空間内での対称性を表す群で、主に結晶構造を表すために使われます。
こちらでは、ヘルマン・モーガン記号(Hermann–Mauguin notation)が使われます。この単に群そのものを表すだけでなく、対称な要素がどんな方向に並んでいるかの情報が含まれます。確かに結晶は、パーツの対称性がどうあるかだけでなく、それがどう並んでいるかによっても区別されますね。
例えば、ヒスイ輝石は「C2/c」と表されるそうです。詳しくは「ヘルマン・モーガン記号の解読 – 日本結晶学会誌」など参照。
また、壁紙やタイルの模様などのパターンは、模様群として調べられているようです。
ここまで、二面体群、多面体群、点群・結晶群を紹介してきました。
群論を使えば、図形や物質・結晶の対称性を簡単に表せます。群論のアイデアは抽象的で、触れたことのない人にとって最初は戸惑うかもしれませんが、今回のような例で少しずつイメージを掴んでもられば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
群論の味わい -置換群で解き明かすルービックキューブと15パズル-
共立出版
売り上げランキング: 391,593
こちらもおすすめ
有限群をケーリーグラフ・乗積表(SageMath)を使って眺めてみよう