どうも、木村(@kimu3_slime)です。
今回は、有限群・ガロア理論を理解するときに基本的な対象である対称群、それに関連する概念である置換、互換、置換の符号、交代群などについて解説します。
対称群、置換とは
対称群\(S_n\)(symmetric group)とは、\(n\)次の置換(permutation)の集まりのなす群です。そして\(n\)次の置換とは、\(n\)個の要素をもつ集合\(X\)からそれ自身への全単射な写像です。
\[ \begin{aligned}S_n:=S (X):=\{f \mid f :X\to X, f \text{は全単射} \}\end{aligned} \]
言い換えれば、置換とは文字の入れ替え操作、\(n\)個の記号列を入れ替える規則のことです。
いきなり言われてもピンと来ないと思うので、具体例を挙げて解説します。
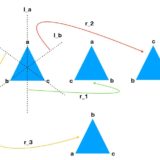
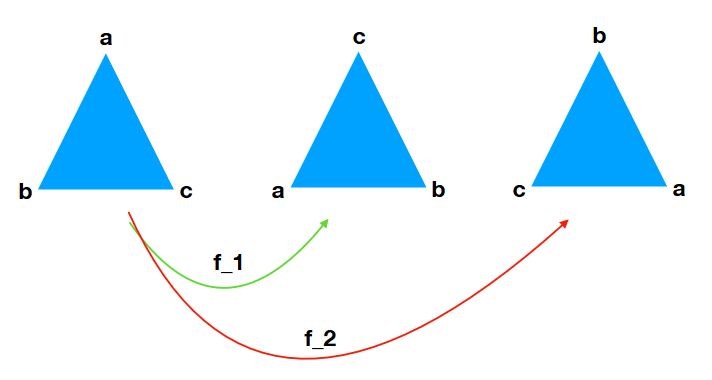
例えば、\(X=\{a,b,c\}\)として、写像\(f_1:X\to X\)を、\(f_1(a)=c,f_1(b)=a,f_1(c)=b\)と定めると、\(f_1\)は\(3\)次の置換で、\(f_1\in S_3\)です。この置換は、次の図で言えば三角形の回転を意味しています。
三角形の回転を表す置換を集めた群を、巡回群\(C_3\)というのでした。巡回群は、一般の置換\(S_3\)のうち特殊なもの(巡回置換)を集めたものです。
また、図形の対称性を表す多面体群\(D_n\)も、対称群の部分群です。
このように、回転や鏡映といった操作をより抽象化し、有限文字列の可能な入れ替え(置換)全体を考えたものが対称群\(S_n\)となっています。
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説、図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説
置換は、対応関係がわかりやすくなるように、次のように表すことがあります(二行記法)。
\[ \begin{aligned}f_1=\begin{pmatrix} a & b & c\\ c& a& b \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}\end{aligned} \]
置換となる記号の集まり\(X\)は、アルファベットでも数字でも、何で書いても本質的には同じです(要素数が同じなら、\(S(X)\simeq S(X^{\prime})\)となるので)。
何番目の記号を指しているのかわかりやすいので、数字の集合\(X=\{1,2,\dots,n\}\)が使われることが多いです。この記事でもそうしましょう。
置換はあみだくじと同一視できます。\(f_1\)ならば、次の図のようになります(\(a,b,c\)ではなく\(1,2,3\)と書くことにする)。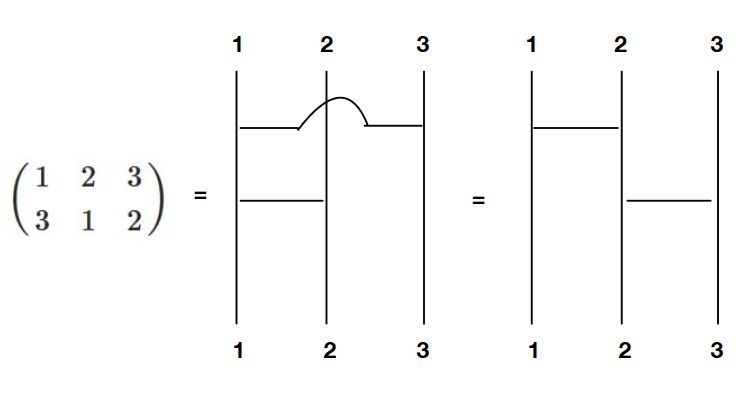
あみだくじは、上側にある文字\(1,2,\dots,n\)を入れ替えるという意味で置換です。何も入れ替えない置換、すなわち恒等置換(単位置換)\(e\)は、あみだくじで言えば何も横線の入っていないものと見なせます。
\[ \begin{aligned}e=\begin{pmatrix} 1 & 2 & 3\\ 1& 2& 3 \end{pmatrix}\end{aligned} \]
任意の置換には、逆写像があります。それは逆置換と呼ばれます。
\[ \begin{aligned}f_1^{-1}=\begin{pmatrix} 1 & 2 & 3\\ 2& 3& 1 \end{pmatrix}\end{aligned} \]
もとのあみだくじを、逆さま(下から上に辿る)ものとして見たものが逆置換です。
置換と置換の積とは、置換の写像としての合成と約束します。\(gf:=g\circ f\)と、積の順序、積の記号を省略することに気をつけてください。あみだくじで言えば、積とはあみだくじを上下につなげてできるあみだくじのことです。
この積に関して、\(S_n\)は群となります。\(n \geq 3\)のとき、\(S_n\)は可換ではありません。例えば次のようになるので。
\[ \begin{aligned} \begin{pmatrix} 1 & 2 &3 \\ 3 & 1 &2 \end{pmatrix} \begin{pmatrix} 1 & 2 &3 \\ 2 & 1 &3 \end{pmatrix} = \begin{pmatrix} 1 & 2 &3 \\ 1 & 3 &2\end{pmatrix}\end{aligned} \]
\[ \begin{aligned} \begin{pmatrix} 1 & 2 &3 \\ 2 & 1 &3 \end{pmatrix} \begin{pmatrix} 1 & 2 &3 \\ 3 & 1 &2 \end{pmatrix} = \begin{pmatrix} 1 & 2 &3 \\ 3 & 2 &1 \end{pmatrix}\end{aligned} \]
(これは\(D_3\)において、回転と鏡映が可換でないことと同じです。\(S_3 \simeq D_3\)となっています)
互換、巡回置換
置換の性質を調べるために、特殊な性質を持った置換に名前をつけましょう。
\(X\)の2つの要素\(a,b\)のみを入れ替え、他を入れ替えない置換を互換(transposition)と言い、\(\begin{pmatrix} a & b \end{pmatrix}\)と書きます。例えば次のように。
\[ \begin{aligned}\begin{pmatrix} 1 & 2 \end{pmatrix}= \begin{pmatrix} 1 & 2 & 3\\ 2& 1& 3 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix}a & b \end{pmatrix}=\begin{pmatrix} \dots & a &\dots &b &\dots \\ \dots& b& \dots&a & \dots \end{pmatrix}\end{aligned} \]
次数\(n\)が何であっても、任意の置換は、互換の積として表せます。
(任意の置換\(f\)に対し、\(f(i)\neq j\)なる部分で\(i,j\)を入れ替える互換をかけていけば単位置換に変形できます。厳密には数学的帰納法で示せます。)
さきほどの置換\(f\)は、次のように互換の積として表せます。
\[ \begin{aligned}\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}=\begin{pmatrix} 2 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 \end{pmatrix}\end{aligned} \]
さらには、任意の置換は、\(\begin{pmatrix} k & k+1 \end{pmatrix}\)のタイプの互換(隣接互換)の積として表せます(あみだくじの原理)。
(互換の積を、\(\begin{pmatrix} k & k+1 \end{pmatrix}\)のタイプの互換の積として表せれば良いわけです。例えば\(\begin{pmatrix} k & k+2 \end{pmatrix} =\begin{pmatrix} k & k+1 \end{pmatrix} \begin{pmatrix} k+1 & k+2 \end{pmatrix} \begin{pmatrix} k & k+1 \end{pmatrix} \)です。より一般の互換も同様に分解できますね。)
あみだくじの原理は、複雑なあみだくじ(何本か縦線を飛び越える横線のあるあみだくじ)も、等価で単純なあみだくじ(隣り合う横線のみであるあみだくじ)として書き換えられるという主張ですね。
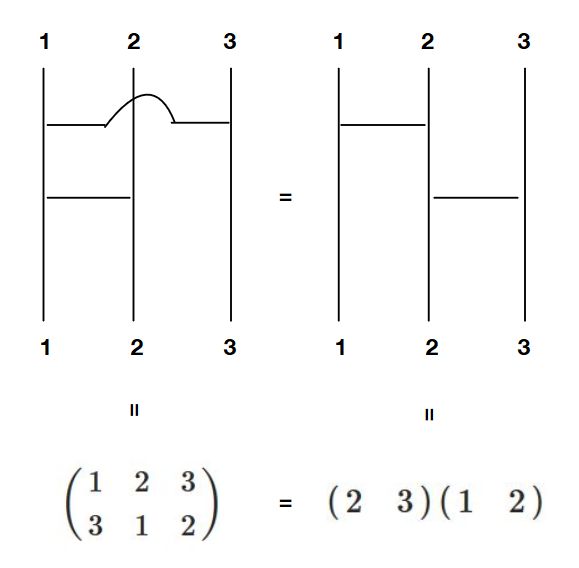
\(f\)は番号を順に入れ替える置換で、\(f^3=e\)という性質を持っています。このような置換を、巡回置換(cyclic permutation)と言います。
より一般には、\(i_1,i_2,\dots,i_r \in \{1,2,\dots,n\}, r\geq 2 \)をそれぞれ異なる要素として、\(f(i_1)=i_2,f(i_2)=i_3,\dots,f(i_{r-1})=i_r,f(i_r)=i_1\)で、他の要素を変えない置換\(f\)を長さ\(r\)の巡回置換と呼び、\(f=\begin{pmatrix} i_1 & i_2 &\dots & i_r \end{pmatrix}\)と書きます。
\[ \begin{aligned}\begin{pmatrix} i_1 & i_2 &\dots & i_r \end{pmatrix}=\begin{pmatrix} \dots & i_1 &\dots &i_k &\dots &i_r&\dots \\ \dots& i_2& \dots&i_{k+1} & \dots & i_1 &\dots \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}=\begin{pmatrix} 3 & 2 &1 \end{pmatrix}=\begin{pmatrix} 1 & 3 &2 \end{pmatrix}\end{aligned} \]
長さ\(r\)の巡回置換を集めた集合は群をなし、それを巡回群\(C_r\)と呼ぶのでした。
「互換とは、長さ\(2\)の巡回置換である」とも言えますね。
ケイリーの定理
対称群\(S_n\)は、ある意味で、すべての有限群の母です。
ケイリー(Cayley)の定理
任意の有限群は、対称群の部分群と群として同型。
証明しましょう。任意の有限群を\(G\)として、\(G\)と\(S(G)\)の部分群が同型であることを示します。
\(g\in G\)に対して、写像\(L_g:G\to G\)を\(L_g(a)=ga\)と定めると、\(L_g\)は\(G\)上の置換です。
\(L_g(a)=L_g(b)\)とすると\(ga=gb\)、\(g^{-1}\)をかければ\(a=b\)で単射。任意の\(h \in G\)は、\(L_g(g^{-1}h)=h\)と表せるので全射。
そして、\(F:G\to S(G)\)を、\(g\mapsto L_g\)によって定めると、\(F\)は単射な準同型写像です。
\(F(g)=F(h)\)と仮定すると、\(L_g=L_h\)なので、\(g=L_g(e)=L_h(e)=g\)で単射。また、\(L_{gh}(a)= gh a =g(L_h(a))=L_g(L_h(a))\)なので、\(F(gh)=L_{gh}=L_g L_h = F(g)F(h)\)で準同型。
よって、\(G \simeq F(S(G))\)が言えました(群の準同型写像による像は、常に部分群となるので、\(F(S(G))\)は\(S(G)\)の部分群)。
有限群\(G\)において\(g\)をかける操作(\(g\)による\(G\)の左移動という)は、\(G\)の置換と同一視できる、というアイデアです。つまり、有限群の演算は、置換の一種だとみなせるわけですね。
対称群の位数(要素の個数)は\(n!\)で、非常に大きいです。それだけ対称群は、多様な「規則」を含んでいます。
ガロア理論と対称群
対称群\(S_n\)は、ガロア理論(Galois theory)においても重要な役割を果たします。
高校の数学で、2次方程式\(ax ^2 + bx +c =0\)の解の公式を習うと思います。3次方程式、4次方程式でも解の公式が存在することが知られています(カルダノの公式、フェラーリの方法)。この調子なら5次方程式にも解の公式がありそうだと思えるかもしれませんが、実は、(一般の)5次方程式には解の公式が存在しません(解の公式がない=四則演算とべき乗根を使って解を表示できない)。この事実は、アーベル–ルフィニの定理(Abel–Ruffini theorem)と呼ばれています。
「5次方程式の解の公式は存在しない」のはなぜか。それに明快な答えを与える理論が、エヴァリスト・ガロアらによって築かれたガロア理論です。このガロアの発見が、群論が生まれ、整備されていくきっかけになったと言われています。
むしろ、現在群論と呼ばれている分野は、もともとは方程式の研究、方程式論から生まれてきた部分があると見れるでしょう。(それだけが群論ではないのですが…)
置換というアイデアも、群論が生まれる前、ラグランジュやコーシーが方程式の解の公式を調べるうちに見いだされたものです。また、早い時期にガロア理論をまとめた本として、1870年に発表されたジョルダンによる本の名は、「置換と代数方程式論(Traité des substitutions et des équations algebraique)」です。
このように、置換、もとい対称群の役割は歴史的にも大きいことがわかります。
参考:群論・ガロア理論の一歩手前から学ぶ 「アーベルの証明」レビュー
群論の歴史について、この文章は面白かったです:いわゆる「ラグランジュの定理」について – 赤堀庸子
ガロア理論では、方程式が解の公式によって解けるかどうかという問題(可解性)を、(ガロア群と呼ばれる)群の性質に対応させられます。
ガロア群が可解群(という性質を持つ)ならば、方程式はべき根によって解けない。
そして、\(n\)次の(一般)多項式のガロア群は対称群\(S_n\)に同型で、\(n\geq 5\)ならば\(S_n\)が可解でないことが示せるのです。
可解群という性質は、その群がどんな正規部分群を持つかによって決まるものです。つまり、\(S_n\)の正規部分群を調べることになります。
そこで登場するのが、偶置換を集めた群、交代群\(A_n\)です。これを説明するため、置換の符号なるものを考えましょう。
置換の符号、偶置換、奇置換
さきほど、「任意の置換は互換の積に表せる」という話をしました。この表し方は一意ではありませんが、積に登場する互換の個数が偶数か奇数かどうかは、置換によって一意に定まります。
偶数個の互換の積で表せる置換を偶置換(even permutation)、奇数個のときは奇置換(odd permutation)と呼びます。
そして、\(\mathrm{sgn}: S_n \to \{1,-1\}\)を
\[ \begin{aligned}\mathrm{sgn}(f):= \prod _{1 \leq i<j\leq n} \frac{f(i)-f(j)}{i-j}\end{aligned} \]
によって定め、\(\mathrm{sgn}(f)\)を\(f\)の符号と呼びます。偶置換ならば\(1\)、奇置換ならば\(-1\)となるよう定まっています。この符号の定義は、行列式の符号による定義でも使われますね。
さらに、\(\mathrm{sgn}\)は、2つの要素からなる群\(\{1,-1\}\)への準同型写像であることが示せます。
例を見てみましょう。次の置換は、2つの互換の積で表せるので偶置換です。符号もきちんと一致しています。
\[ \begin{aligned}\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}=\begin{pmatrix} 2 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned} \mathrm{sgn}(f)&= \prod _{1\leq i< j \leq 3} \frac{f(i)-f(j)}{i-j}\\&= \frac{f(1)-f(2)}{1-2}\frac{f(1)-f(3)}{1-3}\frac{f(2)-f(3)}{2-3}\\&= \frac{2}{-1} \frac{1}{-2} \frac{-1}{-1}\\ &= 1 \end{aligned} \]
符号の定義式は、少しわかりにくいかもしれません。計算例を見ればわかるように、\(\frac{f(i)-f(j)}{i-j}\)は、番号を交代させていれば\(-1\)、交代していなければ\(+1\)を生み出します。こうして番号交代の回数=互換の総数をカウントし、積を取ることによってその遇奇性=符号が計算できています。
(置換は、行列として表現することができます。置換\(f\)に対し、\(n\times n\)の行列で、\(j\)行\(f(j)\)列のみが\(1\)、他が\(0\)の行列を置換行列\(A_f\)と言います。置換の符号は置換行列の行列式と対応しています \(\mathrm{sgn}(f)= \det (A_f)\))
交代群
\(n\)次の偶置換を集めた群が、交代群(alternating group)\(A_n\)です。
交代群\(A_n\)は、対称群\(S_n\)の正規部分群です。(交代群は符号の核\(A_n = \mathrm{Ker}(\mathrm{sgn})= \mathrm{sgn}^{-1}(\{1\})\)で、準同型写像の核は正規部分群となるので。)
\(A_1\)は自明な群、\(A_2\)は2つの要素からなる群、\(A_3\)は巡回群\(C_3\)に同型です。したがって、興味深いのは\(n\geq 4\)のときになります。
\(n\geq4\)のとき、\(A_n\)は非可換群となります。\(n=4\)ならば、次のように。
\(\begin{pmatrix} 1 & 2 &3 \end{pmatrix}= \begin{pmatrix} 2 &3 \end{pmatrix}\begin{pmatrix} 1 & 2 \end{pmatrix} \in A_4\)、\(\begin{pmatrix} 2 & 3 &4 \end{pmatrix}=\begin{pmatrix} 3 &4 \end{pmatrix}\begin{pmatrix} 2 & 3 \end{pmatrix}\in A_4\)ですが、
\[ \begin{aligned} \begin{pmatrix} 1 & 2 &3 \end{pmatrix}\begin{pmatrix} 2 & 3 &4 \end{pmatrix}&=\begin{pmatrix} 1 & 2 &3 \end{pmatrix}\begin{pmatrix} 1&2 & 3 &4 \\ 1&4 & 2 &3 \end{pmatrix} \\&= \begin{pmatrix} 1&2 & 3 &4 \\ 2&1 & 4 &3 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned} \begin{pmatrix} 2 & 3 &4 \end{pmatrix}\begin{pmatrix} 1 & 2 &3\end{pmatrix} &= \begin{pmatrix} 2 & 3 &4 \end{pmatrix}\begin{pmatrix} 1&2 & 3 &4 \\ 3&1 & 2 &4 \end{pmatrix} \\ &= \begin{pmatrix} 1&2 & 3 &4 \\ 3&4 & 1 &2 \end{pmatrix} \end{aligned} \]
となるので。
ガロア理論において、群とその正規部分群を調べることは重要、という話をしました。\(S_n\)は、\(n\neq 1,4\)のとき、全体、単位群、交代群のほかに正規部分群を持たないことが知られています。
また、\(A_5\)は単純群(自明でない正規部分群を持たない)であり、可解群でないことが示せます。可解群の部分群は可解なので、ここから\(S_5\)が可解でないと言えるのです。(実は、要素数が最も少ない非可換な単純群は、交代群\(A_5\)です)
まとめ
置換:有限集合からそれ自身への全単射。文字の入れ替え。
対称群:置換を集めた群。演算は写像の合成。
互換:2つの要素のみ入れ替える置換。一般化として巡回置換がある。
ケーリーの定理:任意の有限群は、対称群の部分群と同型。
置換の符号:置換を互換の積として表すとき、現れる互換の回数によって定まるもの。
交代群:偶置換のなす群。
対称群、交代群とその例や基本概念を紹介してきました。
後半は事実のみ述べることが多くなりましたが、前半の置換の話がまず理解できていれば良いと思います。
任意の有限群は対称群の部分群として同型(ケイリーの定理)で、ガロア理論の理解にも欠かせないので、対称群は重要であると感じ取っていただけたのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
群論の味わい -置換群で解き明かすルービックキューブと15パズル-
共立出版
売り上げランキング: 391,593
こちらもおすすめ
図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説
有限群をケーリーグラフ・乗積表(SageMath)を使って眺めてみよう
群論・ガロア理論の一歩手前から学ぶ 「アーベルの証明」レビュー