どうも、木村(@kimu3_slime)です。
数学ー特に代数学ーの歴史を知りたくて、「アーベルの証明―「解けない方程式」を解く」を読みました。
タイトルからするとアーベルという人物ピンポイントを紹介する本に見えますが、そんなことはありません。無理数-ピタゴラスの話から始め、アーベルの発見に至るまでの流れが書かれています。
アーベルが証明したことは、「五次方程式に解の公式(代数的な解)がない」ということです。これに関連して、ガロアが群論・ガロア理論と呼ばれる理論を生みだし、それは代数学における革命となりました。
ガロア理論は、大学の数学科では2-3年次に教えられる内容で、一般の解説書も多く書かれています(例えば天才ガロアの発想力や数学ガール)。
しかしながら、大学の数学に触れたことがない人が、いきなりガロア理論(群論や体論)に手を出すのは、抽象的で難しいのではないか、と僕は思います。(挫折してみるのもそれはそれで良いですが、できれば理解に近づきたいものです)
そういう意味で、「アーベルの証明―「解けない方程式」を解く」はガロア理論の手前までの数学を扱った本として、おすすめです。
知らなかった代数学の歴史
代数学(algebra)は、数を\(x,y,z\)など文字で表して調べる分野です。
例えば、中学高校で習う2次方程式(移項や因数分解、解の公式)は、700-900年頃のアラビアの数学者、アルフワリズミが生みだしたものの影響が大きいと言われています。アルフワリズミは、アルゴリズムの語源となったと言われる。
……といったことは、この本を読む前から調べて知っていました。しかし、次のようなことは知らなかったので、驚きました。
・商業の栄えた中世のアラビア、ヨーロッパで簿記(お金やものの出入りの記録法)が生まれ、そこでアラビア数字や代数学が必要とされる。2次方程式は、「実用的な数学」だった。ゼロの導入もこの頃。
・プラス(+)マイナス(-)の記号は、黒字と赤字を表す記号だったが、1400年代に数学に輸入された。その前、5プラス3などと自然言語を含んだ文章で書かれていた。
・ヴィエト(1500-1600年)の貢献の大きさ。未知数や平方\(\sqrt{} \)を記号で表した。係数(coefficient)という考え方も彼によるもの。それまでは基本的に\(x^2 + 3x+ 2=0\)という具体的な方程式を解くものであったが、\(a x^2 + bx+ c=0\)という一般の方程式が簡単に扱える。
・負の数は1600年代になってようやく数として認められ始める。例えば、\(x^2=4\)の解は\(x=2\)のみであった(現在で言えば\(x=-2\)も解)。デカルトは負の数を「偽数、つまりゼロより小さい数」と呼んだし、ラプラスは「マイナスかけるマイナスはプラス」のルールを「いくらか困難がある」と述べた。
これらを知ると、中学生になって、\(x,y\)を使った方程式や、マイナスの理解につまづく人が少なくないのも納得です。例えばユークリッドの幾何学からすれば2000年近く後になって、人類の知られるところになったわけですから。
今「当たり前」として学校で知られていることも、昔の人々・数学者が悩んだ結果というわけです。
そのことを知れば、数学で何かわからないことがあっても、臆せず少しずつ理解してみよう、という気になりませんか?
「アーベルの証明―「解けない方程式」を解く」は、次のような章立てです。
1章 無理数スキャンダル
2章 論争と係数
3章 不可能性と虚数
4章 螺旋と海岸線
5章 予感と置換
6章 アーベルの証明
7章 アーベルとガロア
8章 対称性を見る
9章 ものの順序
10章 解けないものを解く
付録A アーベルの1824年の論文
付録B アーベルによる代数的解の一般系の議論
付録C 置換に関するコーシーの定理
解の公式を見つけるにあたり、方程式の文字を入れ替える「置換」という操作が生み出され、置換によって変わらない式が大事だとわかってきました。
これは後に、置換群(対称群\(S_n\))として知られるものですが、その視覚的なイメージが本では紹介されています。
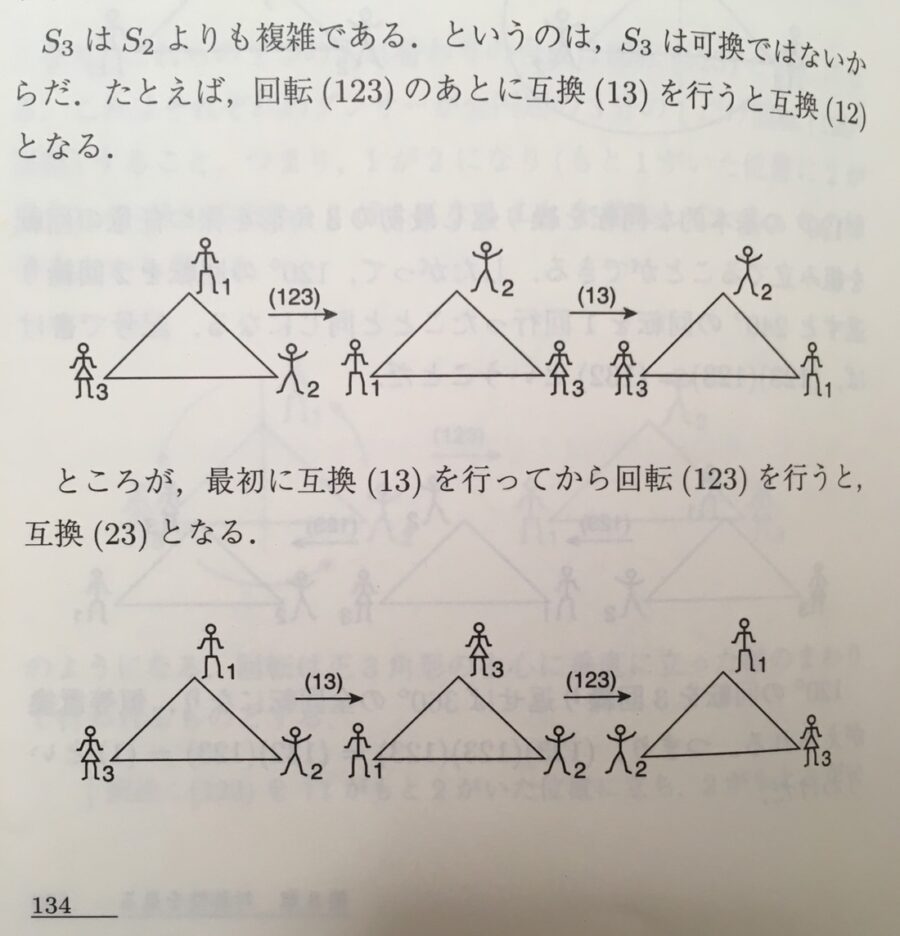
画像引用:アーベルの証明―「解けない方程式」を解く
「アーベルの証明」は、証明やガロア理論に踏み込むには、ちょっと準備が足りないと感じます。ちゃんと学ぶなら、教科書(雪江や松坂)を読むべきでしょう。しかしながら、そこに至るまでの多くの数学者の迷いと歩みが、読み物としてよく書かれています。
群論・ガロア理論について何も知らないけど、なんとなく興味がある……そんな人におすすめです。
木村すらいむ(@kimu3_slime)でした。ではでは。
日本評論社
売り上げランキング: 971,474
こちらもおすすめ
「数学をつくった人びと」レビュー:数千年受け継がれてきた数学
厳密さ・証明が現代数学で要求されるのはなぜ? 近代数学の歴史をたどる






