どうも、木村(@kimu3_slime)です。
「大学数学のお作法と無作法」という本を読みました。
この記事の続きのような話をします:「趣味の大学数学」は、厳密化・抽象化だけをありがたがらない
数学にはお作法:厳密、証明がある
大学数学が苦手になるのは、数学の「お作法」を知らないから。
そのお作法を、数学の教科書で示されるような枠組みだけでなく、論理的な言葉、数学の歴史によっても紹介している本です。
著者は大学で理工系教養の数学の講義を長年担当していて、その経験が生きてか、数学科のためだけでない数学、理工系数学の姿がバランスよく示されています。
微積分と線形代数はもちろん、微分方程式・フーリエ解析・複素解析、論理・集合・位相空間といった発展的な話題を含みつつ、広く応用される確率と統計、情報数学(数値解析、アルゴリズム)までカバー。
僕がもし大学数学を初学者に向けて講義するとしたら、この本を下敷きのひとつにしたいです。「微積分、線形代数」の教科書・講義ではカバーされない現代的な教養数学をコンパクトにまとめつつも、応用だけを指向することなく厳密で高度な数学への招待となっています。
第1章 始めに
第2章 言葉の重要性
第3章 数学が分かるとはどういうことか:無作法の勧め
第4章 数学のお作法
第5章 無作法のお作法:近似、精度、誤差、アルゴリズム
第6章 統計現象の取り扱い:バラついた値と集団の性質
第7章 歴史から学ぶ証明の重要性
第8章 数学は役に立たない?
この本は、「数学があまり得意ではない人、何に役立つのかわからないから勉強する気になれないと思う人に読んでほしい」と書かれています。
1,2,4,7,8章は読み物として書かれていて、特にそのような人向けとなっています。
3,5,6章は、解析学、情報数学、確率統計の用語をコンパクトにまとめた……といった文章であり、少しむずかしい印象です。この本で用語やテーマを知り、他の教科書できちんと学ぶための入り口として使えるでしょう。
厳密な証明はなぜ数学に必要とされるようになったか
「大学数学のお作法と無作法」は良い本ですが、だからこそ僕の観点から、批判的に読み解きたい部分があります。
僕なりにまとめるとこうです。
数学という言葉は重要である。それは形式言語としての側面を持っていて、「限りなく近づく」「任意の」といった用語を厳密に使い、実験ではなく論証(証明)によって結果を得る。
厳密さと証明が数学に関して求められる能力であることは、僕も同意です。論理的な文章を書ける能力が、科学を志す学生にとって重要だということも、良い指摘だと思います。
(数学科ではない人が)道具として数学を使う上でも、ある程度の厳密さを扱えるのが大事というのも同意。この本はあくまで、この立場でした。
しかしながら、なぜ厳密さや証明が数学において必要なのかは明確に本では示されていなかったと感じます。半ば当たり前に重要であり、その心をどう理解してもらうか……という視点で書かれていた。
証明が必要とされる理由として、日本の伝統数学(和算)における証明の欠如が挙げられていました。和算が素晴らしい結果を残したにもかかわらず現代数学とあまり交わりがない理由(のひとつ)は、証明がないからだと。もちろん、近代的で共有されうる科学活動にもっていくためには、証明は必要でしょう。
これは、近代-現代数学で殊更にに厳密さや証明が求められる理由としては、十分ではないと思います。
例えばp.91では「連続であるが至るところで微分不可能な関数(ワイエルシュトラス関数)」が紹介されていましたが、まさにこのような例が、数学に厳密さを要求しています。これは「解析学の厳密化」の話ですが、(紙面の問題かもしれませんが)本ではあまり書かれていません。
現代的なレベルでの厳密さは、決して数学本性の自明なものではありません。例えば、1806年頃でさえ「任意の関数は有限個の例外点を除いてすべての点では微分可能である」という「定理」が知られていたのです。
厳密さや証明が数学において強く求められるような歴史的背景を、僕なりにまとめました。
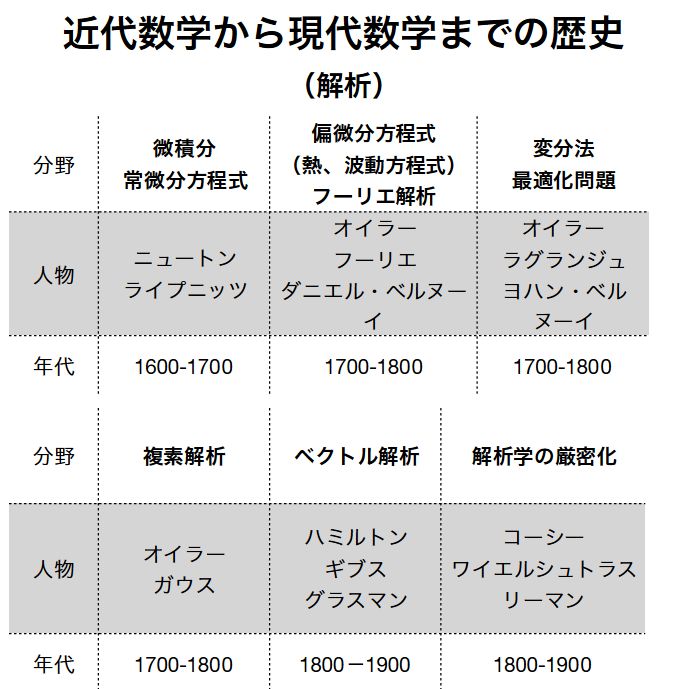

(人物はもっと名を挙げたい人がいますが、キリがないので数人に留めています)
解析学の厳密化
最初に挙げられるのは、解析学の厳密化です。
なぜ厳密化しなければならないかといえば、微分や積分の基礎となる極限や連続性(無限)の扱いが難しいことが徐々にわかっていくからです。
例えばニュートンは「無限小」という概念を用いていて、現在では厳密でないと言われていますが、それでも当時としては微積分は成り立っていたのです。この批判としてコーシーは厳密な解析学を組み立てていきます。
極限に関するチャレンジングな問題提起としては、フーリエが熱伝導方程式を通じて提唱した、「すべての関数は三角関数の和で展開できる」というもの。「級数で定義される関数」は、極限でどのように収束されるかという問題を考えて初めて、一様収束の概念が浮かび上がってきます。
本では厳密化の例として、イプシロン-デルタ論法が挙げられていましたが、これは1860年頃、ワイエルシュトラスによるものと言われています。微積分学の発見んから、数学者の世界でも200年かかっていることなのです。
微積分学のわかりにくいの理由は、ニュートン・ライプニッツから1800年くらいまでのそこまで厳密さが要求されない頃の解析学と、コーシー・ワイエルシュトラス・リーマンあたりの1800年代以降の厳密化した解析学が混ざっていることだと思います。
数学の基礎付け、構造主義
証明が重要である理由は、解析学の厳密化だけでないでしょう。
ひとつは数学の基礎づけです。1850年以降にカントールによって生み出された集合論を通して、ラッセルのパラドックスなどのパラドックスが見つかってきます。こうして数学の基礎への疑問に応じ、ヒルベルトはヒルベルト・プログラムを打ち出し、そこから証明論・数理論理学と呼ばれる領域が生まれる。
論理と集合をベースとして数学は一新されました。
参考:集合論入門:集合の定義、数の集合、ラッセルのパラドックス、数学における証明とは、健全性、完全性とは?、「ゲーデルの不完全性定理」を誤解しないために、数学の歴史的流れを解説
もうひとつは公理的・構造的な数学の台頭です。
非ユークリッド幾何の発見により、議論の出発点となる公理の恣意性が意識されるようになります。現実に依存しない形式的な数学という側面は、この公理主義において強く見られるものです。
次いで、特定の具体的な対象(空間や群)ではなく、ある構造を持った対象すべてを調べる数学分野が発展してきます。いわゆる、抽象空間論(位相空間論)や、抽象代数学です。応用との関連なしに数学が成立するようになればなるほど、証明はより欠かせないものになっていきます。
厳密さや論証が重視されるスタイルが数学全体に広まった理由としては、1900年以降、ブルバキが解析学を厳密に公理的アプローチで組み立てようとした「数学原論」のスタイルが、多くの数学者や教科書に引き継がれたこともあるでしょう。
参考:なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響
厳密さ、証明は段階的に学ばれるもの
改めて、自分なりに数学の歴史をまとめ、考えがまとまってきました。
高校数学から大学数学には、1600-1900年のおよそ300年くらいの、厳密さと証明・論理に関して大きなギャップがあります。「大学数学のお作法と無作法」のように「厳密さと証明」が重要だと教えてあげるのは良いことです。
厳密さ、証明は数学の大事な要素ですが、それは歴史的に時間をかけて知られてきたことです。決して当たり前のものではないし、ステップを飛ばせば理解できない学生がいるのももっともです。
映画の「奇蹟がくれた数式」で描かれていますが、「インドの魔術師」として知られるラマヌジャンは、ヨーロッパの数学にふれるまでは、証明の必要性を知りません。
それでありながら、直感を用いて優れた結果に到達しています。ハーディの助け、証明という手段がなければ、ラマヌジャンの結果がパブリッシュされ数学の体系になかったとはいえ。「だから証明は重要でない」とは言いませんが、証明がなかったからといってラマヌジャンの仕事が数学において意味がないともまた、思いません。
僕とは理由が違うかもしれませんが、物理学者によるこんな文章もあります:僕は、厳密な理論は、たいてい嫌いです
「大学数学のお作法と無作法」でも、理論的な「お作法」は知った上で、コンピュータによる「無作法」、イメージを描いて数学を理解することが推奨されています。
当サイト「趣味の大学数学」では、「数学とは厳密なものである」だけではない部分も含め、数学……というか数理科学全般を描き出したいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
筑摩書房
売り上げランキング: 664,478
こちらもおすすめ
「わかりやすい」だけでなく、面白くきちんとした数学を伝えたい
「ゲーデルの不完全性定理」を誤解しないために、数学の歴史的流れを解説
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響