どうも、木村(@kimu3_slime)です。
今回は、2変数のテイラー展開とはなにか、その計算例を紹介します。
2変数のテイラー展開
1変数の関数\(f(x)\)は、適度に微分可能ならば、
\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots \\+ \frac{f^{(n)}(a)}{n!}(x-a)^n + R_{n+1}(x)\end{aligned} \]
\[ \begin{aligned}R_{n+1}(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\end{aligned} \]
2変数の関数\(f(x,y)\)についても、\(x,y\)を使った多項式としてテイラー展開できます。\(p_0=(a,b)\)におけるテイラーの定理は、
\[ \begin{aligned}f(x,y)=f(a,b)+f_x(a,b) (x-a)+f_y(a,b)(y-b)+\cdots \\ \frac{1}{n!}((x-a)\frac{\partial}{\partial x} +(y-b)\frac{\partial }{\partial y})^n f(a,b) + R_{n+1}(x) \end{aligned} \]
\[ \begin{aligned} R_{n+1}(x)=\frac{1}{(n+1)!}((x-a)\frac{\partial}{\partial x} +(y-b)\frac{\partial }{\partial y})^{n+1} f(a+\theta x,b +\theta y)\end{aligned} \]
を満たす\(0<\theta <1\)が存在するという主張です。
一般項が、\(\frac{\partial}{\partial x}\)といった偏微分作用素を使って書かれていることに注意しましょう。\(n=2\)ならば、
\[ \begin{aligned} \frac{1}{2!}((x-a)\frac{\partial}{\partial x} +(y-b)\frac{\partial }{\partial y})^2 f(a,b) \\=\frac{1}{2}\{ f_{xx}(a,b)(x-a)^2 +f_{xy}(a,b)(x-a)(y-b)\\+f_{yx}(a,b)(x-a)(y-b) +f_{yy}(a,b)(y-b)^2\} \end{aligned} \]
です。\(\frac{\partial}{\partial x} f (a,b)\)とは、\(f\)の\(x\)偏導関数\(f_x(x,y)\)の点\(a,b\)における値であり、定数関数\(f(a,b)\)の偏微分ではありません。1変数のときと同様、多項式の係数には\(f\)の導関数の値が登場しています。
2変数のテイラーの定理の証明は、1変数の平均値の定理に帰着させます。杉浦「解析入門 Ⅰ」p.147などを参照。
テイラー展開の例
多変数となると記号が多くて厄介に見えますが、テイラー展開は計算してみれば怖いものではなく便利です。
\(f(x,y)=\sin x \sin y\)を\(p_0=(0,0)\)で2次までテイラー展開してみます。(この\(f\)は、波動方程式の解:定常波の例です)
最初にやることは、偏導関数の値を調べることです。
\[ \begin{aligned}f_x =\cos x \sin y, f_y = \sin x \cos y\end{aligned} \]
\[ \begin{aligned}f_{xx} =-\sin x \sin y,f_{xy}=f_{yx}=\cos x \cos y,f_{yy}=-\sin x \sin y \end{aligned} \]
なので、
\[ \begin{aligned}f_x(p) = f_y (p)= 0\end{aligned} \]
\[ \begin{aligned}f_{xx} =f_{yy}=0,f_{xy}=f_{yx}=1\end{aligned} \]
となり、2次までのテイラー展開は
\[ \begin{aligned}0+0+\frac{1}{2}(0x^2+xy+xy+0y^2)= xy\end{aligned} \]
となります。これは双曲放物面です。
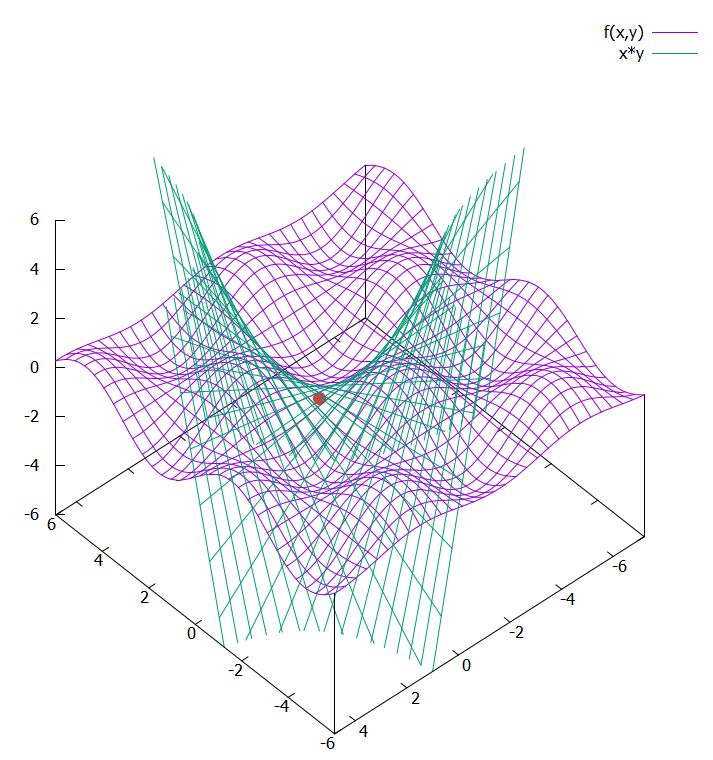
別の例として、\(g(x,y)=e^{-(x^2+y^2)}\)の\(p_0=(0,0)\)における2次までのテイラー展開を求めてみます。(\(g\)は多変数のガウス関数です)
\[ \begin{aligned}g_x = -2x g,g_y =-2y g\end{aligned} \]
\[ \begin{aligned}g_{xx}=-2 g-2x g_{x},g_{yy}=-2g-2yg_y,g_{xy}=g_{yx}=4xy g\end{aligned} \]
なので、
\[ \begin{aligned}g_x(p) =g_y(p) =0\end{aligned} \]
\[ \begin{aligned}g_{xx}(p)=g_{yy}(p)=-2,g_{xy}(p)=g_{yx}(p)=0\end{aligned} \]
です。よって、2次までのテイラー展開は
\[ \begin{aligned}1+0+\frac{1}{2}(-2x^2 +0 xy-2y^2 )=1-(x^2+y^2)\end{aligned} \]
となりました。

今回の形の\(g\)のテイラー展開では、1変数のテイラー展開
\[ \begin{aligned}e^x =1 + x+ \cdots\end{aligned} \]
に\(x\rightarrow -(x^2+y^2)\)と代入することでも、\(1-(x^2+y^2)\)を求めることができます。
偏微分係数を計算して2変数のテイラー展開を行う方法、1変数のテイラー展開を応用する方法、どちらか楽な方法を選べれば、展開はよりスムーズです。
2次近似の整理:ヘッセ行列
もう一度テイラー展開の一般形に戻り、その意味を捉え直してみましょう。
\[ \begin{aligned}f(a,b)+f_x(a,b) (x-a)+f_y(a,b)(y-b) \end{aligned} \]
また、2次までの項を使った近似は、2次曲面による\(f\)の近似と言えます。
適度に微分可能な2変数関数\(f\)に対し、次の記号を用意しましょう。
\[ \begin{aligned}\nabla f =\mathrm{grad} f = (f_x,f_y)\end{aligned} \]
\[ \begin{aligned}H(f) = \begin{pmatrix} f_{xx} & f_{xy}\\f_{yx}&f_{yy} \end{pmatrix}\end{aligned} \]
\(\nabla f =\mathrm{grad} f\)を\(f\)の勾配ベクトル(gradient vector)、\(H(f)\)を\(f\)のヘッセ行列(Hesse matrix)と言います。
\(p=(x,y),p_0=(a,b)\)として、2次近似は
\[ \begin{aligned}f(p)\simeq f(a,b)+f_x(a,b) (x-a)+f_y(a,b)(y-b)+ \\\frac{1}{2}\{ f_{xx}(a,b)(x-a)^2 +f_{xy}(a,b)(x-a)(y-b)\\+f_{yx}(a,b)(x-a)(y-b) +f_{yy}(a,b)(y-b)^2\}\\ = f(p_0)+\langle\nabla f,(p-p_0) \rangle+\frac{1}{2}\langle (p-p_0) , H(f)(p-p_0) \rangle \end{aligned} \]
と簡単に表されます。ここで\(\langle p,q\rangle\)はベクトルの内積です。
\(x,y\)の2次の項のみからなる多項式\(\frac{1}{2}\langle (p-p_0) , H(f)(p-p_0) \rangle \)は、一般に2次形式と呼ばれます。
1変数関数の極値を調べるために2階導関数を調べたのと同様に、2変数・多変数関数の極値を調べるためには、この2次形式、その係数を成分とするヘッセ行列を調べることが大事です。
参考:2変数関数の極値の求め方、ヘッセ行列とは?、条件付き極値問題:ラグランジュの未定乗数法とは
以上、2変数のテイラー展開とその計算例を紹介してきました。
今回の話は、2変数だけでなく一般の\(N\)変数にも展開できます。
ただしいきなり一般論に進むと難しくなるので、まずは2変数のテイラー展開、2次までの展開がどんなものか慣れてみると良いのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740