どうも、木村(@kimu3_slime)です。
今回は、正規分布として応用されるガウス積分の近似値を、テイラー展開で求める方法を紹介します。
ガウス積分の計算しにくさ
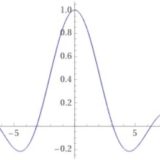
ガウス積分とは、次のような広義積分です。
\[ \begin{aligned}\int_{-\infty} ^{\infty} e^{-x^2}= \sqrt{\pi}\end{aligned} \]
![]()
被積分関数(ガウス関数)\(e^{-x^2}\)を調整した関数は、統計学においては正規分布と呼ばれます。実験における測定誤差など、正規分布に従うような現象は多く、重要な対象です(もちろん正規分布に従わない現象もありますが)。
また、どんな母集団を調査しても、十分に大きなサンプルを取り出すと、母平均とサンプル平均の誤差は正規分布に近似的に従うことが知られています(中心極限定理)。
ガウス積分の式を少し調整すると、
\[ \begin{aligned}\int_{-\infty} ^{\infty}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx= 1\end{aligned} \]
となります。ここで\(\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}\)は、平均が0、分散が1の正規分布で、標準正規分布と呼ばれています。
さて、グラフの全体の面積(=確率)\(1\)はわかっているわけですが、一部分における面積を求めるにはどうしたら良いのでしょうか。
\[ \begin{aligned}\int_{0} ^{1}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx\end{aligned} \]
通常の微積分の知識によれば、\(e^{-x^2}\)の原始関数が求められれば、積分は計算できます。……どんな関数が原始関数になるか思いつきますか?
実は、ガウス関数の原始関数は、初等関数(\(x^n,\sin x,e^x\)といった高校までで習う有名な関数)で表せないことが知られています。
どうやってその積分の値を求めるか。統計学では、あらかじめその値が標準正規分布表として求められており、それを応用して計算することが多いです。例えば\([0,1]\)の範囲の面積は0.3413、つまり約34%であることがわかります。今ならコンピュータでも計算できるでしょう。
今回は、どうしてそのような値になっているのか、積分の近似値を求めて確かめてみましょう。
積分の近似値をテイラー展開で求めよう
\[ \begin{aligned}\int_{0} ^{1}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx\end{aligned} \]
なる積分の近似値を求めましょう。
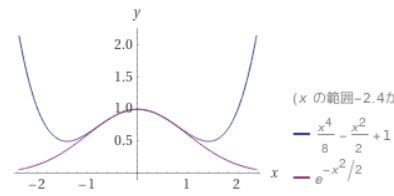
\(e^{-x^2}\)が計算しづらいです。そこで、\(x=0\)まわりのテイラー展開によって多項式になおしてみます。
\[ \begin{aligned}e^{x} = 1+ x+\frac{x^2}{2}+e^c \frac{x^3}{3!}\end{aligned} \]
なので、\(x\)を\(-\frac{x^2}{2}\)に置き換えれば
\[ \begin{aligned}e^{-\frac{x^2}{2}} = 1-\frac{x^2}{2}+\frac{x^4}{8}-e^c \frac{x^6}{2^3\cdot 3!}\end{aligned} \]
となります。ここで\( -\frac{x^2}{2}<c<0\)です。\(x^4\)までの項を使えば、次のようなグラフです。
画像引用:Wolframalpha
\(e^{-\frac{x^2}{2}} \simeq 1-\frac{x^2}{2}+\frac{x^4}{8}\)と近似して、積分を計算してみます。
\[ \begin{aligned} \int_{0} ^{1}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx & \simeq\frac{1}{\sqrt{2 \pi}} \int_{0} ^{1} (1-\frac{x^2}{2}+\frac{x^4}{8} )dx \\ &=\frac{1}{\sqrt{2 \pi}} [x-\frac{x^3}{6} +\frac{x^5}{40}]_0 ^1\\ &=\frac{1}{\sqrt{2 \pi}} \frac{103}{120}\\ & \simeq 0.343 \end{aligned} \]
と、およその大きさは求められています。
その値の正確さは、誤差を調べることでわかります。誤差の大きさは、使わなかった項(剰余項)の積分を評価すれば良いです。\(c<0\)なので、\(e^c \leq e^0=1\)であることに注意して、
\[ \begin{aligned} \int_{0} ^{1}\frac{1}{\sqrt{2 \pi}} e^c \frac{x^6}{2^3\cdot 3!} dx & \leq \frac{1}{\sqrt{2 \pi}} [ e^0 \frac{x^7}{8\cdot 6\cdot 6}]^1 _0\\&= \frac{1}{\sqrt{2 \pi}} \frac{1}{8\cdot 6\cdot 6} \\ & \leq \frac{1}{8\cdot 6\cdot 6}\\ & \leq \frac{1}{100}\end{aligned} \]
となります。つまり、誤差は0.01以下です。
それほど複雑な計算はしていませんが、十分に精度が良い値は求められていますね。テイラー展開の精度をあげれば、もっと精度の良い値を求めることもできます。
もうひとつ、
\[ \begin{aligned}\int_{1} ^{2}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx\end{aligned} \]
の近似値を求めてみましょう。
さきほどのテイラー展開は\(x=0\)まわりだったので、そのまま使うと精度が落ちそうです。\(1\leq x\leq 2\)のとき、\(-2\leq -\frac{x^2}{2} \leq -\frac{1}{2}\)なので、\(x=-1\)におけるテイラー展開を考えてみます。
\[ \begin{aligned}e^{x}=e^{-1}(1+(x+1)+\frac{1}{2}(x+1)^2 +e^{c+1}\frac{(x+1)^3}{3!})\end{aligned} \]
\[ \begin{aligned}e^{-\frac{x^2}{2}}=e^{-1}(2-\frac{x^2}{2}+\frac{1}{2}(-\frac{x^2}{2}+1)^2 +e^{c+1}\frac{(-\frac{x^2}{2}+1)^3}{3!})\\= e^{-1}(\frac{5}{2}-x^2+\frac{x^4}{8} +e^{c+1}\frac{(-\frac{x^2}{2}+1)^3}{3!}) \end{aligned} \]
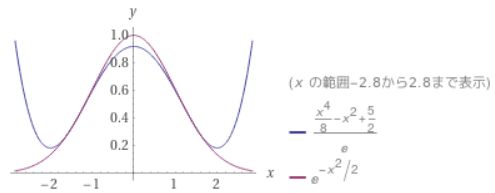
画像引用:WolframAlpha
したがって、積分の近似値は次のようになります。
\[ \begin{aligned} \int_{1} ^{2}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx & \simeq\frac{1}{e\sqrt{2 \pi }} \int_{1} ^{2} (\frac{5}{2}-x^2+\frac{x^4}{8})dx \\ &= \frac{1}{e\sqrt{2 \pi }}[\frac{5}{2}x-\frac{x^3}{3}+\frac{x^5}{40}]_1^2\\ &=\frac{1}{e\sqrt{2 \pi }}(\frac{5}{2}-\frac{7}{3}+\frac{31}{40})\\ & \simeq 0.138 \end{aligned} \]
\(0\leq x \leq 2\)における積分の近似値は、
\[ \begin{aligned}\int_{0} ^{2}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}dx\simeq 0.343+0.138=0.481\end{aligned} \]
となり、標準正規分布表の\(Z=2.00\)における値\( 0.4772 \)に近い値が求められているのがわかりました。
以上、ガウス積分の応用性と計算しにくさを紹介した上で、その近似値をテイラー展開によって求めてみました。
試験の評価で用いられる偏差値は、テストの成績の分布が正規分布であると仮定して、平均が50、標準偏差が10となるように得点を変換して求めた値です。今回の近似計算によって、例えば偏差値50~60の人は全体の約34%で、60~70の人は約14%であることがわかりました(正規分布に従っているならば)。
たとえ積分の厳密な値が求められないときでも、関数をテイラー展開することによってその近似値が求められることが、今回の話で伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080