どうも、木村(@kimu3_slime)です。
高校数学の微分積分では扱わないけれども、大学数学で扱う関数として、双曲線関数\(\cosh ,\sinh ,\tanh \)があります。
今回は、双曲線関数の一種は懸垂線であること、微分と積分の性質を紹介します。
懸垂線としての双曲線関数
\[ \begin{aligned}\cosh x := \frac{e^x +e^{-x}}{2}\end{aligned} \]
により定義される関数は、ハイパボリックコサイン(双曲線余弦関数)と呼ばれます。
そのグラフは、垂れ下がったひも・ケーブルがなす曲線、懸垂線(カテナリー)です。電柱の間をゆるく張られた電線が、このような形をしているのが見て取れるでしょう。

画像引用:Wolframalpha
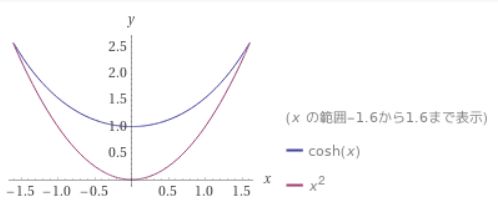
懸垂線は放物線と似ていますが、中心付近の接線の傾きは、懸垂線のほうがゆるやかです。
懸垂線の式は、物理学・力学的に導かれます。
ひもには長さ~重さに応じた重力がかかっていて、それが端点での張る力(張力)と釣り合っているという式が立てられます。\(f(x)\)をそのひもの位置\(x\)における高さとして、そこから得られるのは、次のような微分方程式です。
\[ \begin{aligned}\frac{d^2f}{dx^2}=\sqrt{1+(\frac{df}{dx})^2}\end{aligned} \]
\(\cosh x\)がこの微分方程式を満たしていることを確かめてみましょう。
\[ \begin{aligned}(\cosh x )^{\prime} = \frac{e^x – e^{-x}}{2}=: \sinh x\end{aligned} \]
\[ \begin{aligned}(\cosh x )^{\prime \prime} = \frac{e^x + e^{-x}}{2}=\cosh x\end{aligned} \]
\[ \begin{aligned}1+ ((\cosh x )^{\prime})^2 = 1+\frac{e^{2x}-2+e^{-2x}}{4}=(\cosh x)^2\end{aligned} \]
なので、微分方程式を満たすことが確かめられました。
逆に、\(f(0)=1,f^{\prime}(0)=0\)を満たす微分方程式の解は、必ず\(f(x)=\cosh x\)となることが知られています。
(\(\cosh x\)は、ひもの位置エネルギーを最小にする関数として、変分問題の解としても求められます)
双曲線関数の微分
懸垂線だけでなく、次のように定義されるのが双曲線関数です。
\(\sinh x =\frac{e^x – e^{-x}}{2},\cosh =\frac{e^x +e^{-x}}{2},\tanh x= \frac{\sinh x}{\cosh x}\)
これらはハイパボリックサイン、ハイパボリックコサイン、ハイパボリックタンジェントと呼ばれます。三角関数\(\sin ,\cos , \tan\)に似たような名前と記法です。それは、双曲線関数が三角関数に似た性質を持っているからです。
\[ \begin{aligned}(\cosh x)^2 – (\sinh x)^2 =1\end{aligned} \]
\[ \begin{aligned}\sinh (\alpha +\beta )=\sinh \alpha \cosh \beta +\cosh \alpha \sinh \beta\end{aligned} \]
\[ \begin{aligned}\cosh (\alpha +\beta )=\cosh \alpha \cosh \beta -\sinh \alpha \sinh \beta\end{aligned} \]
\(x^2-y^2 =1\)が双曲線の方程式で、\(\cosh x,\sinh x\)がその関係式を満たすので、双曲線関数と呼ばれるわけですね。
さらには、微分についても良い性質を持ちます。
\[ \begin{aligned}(\cosh x)^{\prime} = \sinh x, (\sinh x)^{\prime}=\cosh x,(\tanh x)^{\prime}=\frac{1}{(\cosh x)^2}\end{aligned} \]
これだけ三角関数と似た性質を持っていれば、類似の記法を採用するのも納得です(笑)。
積分計算への応用
双曲線関数の性質を知っていれば、懸垂線の長さを求めるのは簡単です。
一般に、\(f(x)\)で表される曲線の長さは\(L= \int \sqrt{1+(f^{\prime}(x))^2}dx \)で表されます。
\(f(x)= \cosh x\)とするとき、\(f\)は微分方程式\(\frac{d^2f}{dx^2}=\sqrt{1+(\frac{df}{dx})^2}\)を満たし、また2回微分は\(f^{\prime \prime}(x) =\cosh x\)でした。したがって、
\[ \begin{aligned} L &= \int _0 ^a \sqrt{1+((\cosh x)^{\prime})^2} dx\\ &= \int_0 ^a (\cosh x)^{\prime \prime} dx\\ &= \int_0 ^a \cosh x dx \\ &= [\sinh x]^a _0 \\ &= \sinh a \end{aligned} \]
となります。
さらには、双曲線関数は微分について良い性質を持っているので、その逆関数もまた微分が簡単な形になります。
双曲線関数の(適切な範囲における)逆関数を、\(\mathrm{arcsinh}\, x, \mathrm{arccosh}\, x, \mathrm{arctanh}\, x\)と表しましょう。すると、
\[ \begin{aligned}(\mathrm{arcsinh}\, x)^{\prime} =\frac{1}{\sqrt{x^2+1}}\end{aligned} \]
\[ \begin{aligned}(\mathrm{arccosh}\, x)^{\prime} =\frac{1}{\sqrt{x^2-1}}\end{aligned} \]
\[ \begin{aligned}(\mathrm{arctanh}\, x)^{\prime} =\frac{1}{1-x^2}\end{aligned} \]
が成り立ちます。これを使えば、次のような積分が計算できるわけです。
\[ \begin{aligned}\int _0 ^x\frac{1}{\sqrt{x^2+1}}dx=\mathrm{arcsinh}\, x\end{aligned} \]
特に、逆三角関数と違って、ハイパボリックサインの逆関数は、明示的な式が求められます(\(y = \cosh x\)を、変数変換して\(x\)について解けば良い。)。
\[ \begin{aligned}\mathrm{arcsinh}\, x= \log (x +\sqrt{x^2+1})\end{aligned} \]
また、\(\int _0 ^x\frac{1}{\sqrt{x^2+1}}dx\)のような積分も、\(x=\sinh t\)と置換することで計算できます。これは\(\int \sqrt{1-x^2}dx\)を(逆)三角関数で置換積分して計算できるのと似ていますね。
今回は、懸垂線としての\(\cosh \)、双曲線関数とその微分、積分計算への応用を紹介してきました。
三角関数が微積分に役立つのと同様に、三角関数に似た性質をもった双曲線関数もまた役立ちます。ぜひ、三角関数とセットで双曲線関数も学んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080