逆三角関数をなぜ学ぶか？その微分と積分計算への応用

どうも、木村（@kimu3_slime）です。

高校数学の積分計算において、\(x=\tan \theta\)と三角関数で置換する方法を学びますが、その背景には逆三角関数というものがあります。

今回は、逆三角関数とは何か、その微分と積分計算への応用を紹介します。

三角関数による置換と逆三角関数
逆三角関数とは
逆三角関数の微分と応用
こちらもおすすめ

三角関数による置換と逆三角関数

高校数学では、次のような積分の計算方法を学びます。

\[ \begin{aligned}\int_0 ^1 \frac{1}{x^2+1}dx\end{aligned} \]

\(x=\tan \theta\)と置換します。すると、積分範囲は\(0<\theta<\frac{\pi}{4}\)で、\(\frac{dx}{d\theta} =\frac{1}{(\cos \theta)^2}\)です。したがって、

\[ \begin{aligned} \int_0 ^1 \frac{1}{x^2+1}dx &= \int _0^{\frac{\pi}{4}} \frac{1}{(\tan \theta)^2 +1}\frac{1}{(\cos \theta)^2} d\theta \\ &= \int _0 ^{\frac{\pi}{4}} 1 d\theta \\&= \frac{\pi}{4} \end{aligned} \]

と計算できました。確かに計算できますが、どうしてうまくいくのでしょうか。実は一般に、

\[ \begin{aligned}\int \frac{1}{x^2+1}dx = \arctan x\end{aligned} \]

と表せます。右辺は逆三角関数と呼ばれる関数で、特にタンジェントの逆関数です。

\(\arctan x\)によって、\(\tan x\)の逆関数を表すことにします。逆関数の定義は、\(\arctan (\tan x)=x\)が成り立つこと。

タンジェントの具体値としては、\(\tan 0 =0,\tan \frac{\pi}4=1\)でした。両辺を\(\arctan\)で送ると、\(0 =\arctan(\tan 0)= \arctan 0\)、\(\frac{\pi}4=\arctan(\tan \frac{\pi}4)=\arctan1\)と、\(\arctan x\)の具体値が求まります。

したがって、さきほどの定積分は

\[ \begin{aligned}\int_0 ^{1} \frac{1}{1+x^2}dx = \arctan 1 – \arctan 0 =\frac{\pi}{4}\end{aligned} \]

と計算できます。原始関数がわかっていれば、積分計算は簡単ですね。

逆三角関数とは

\(\tan x\)の逆関数を考えるときには、注意すべきことがあります。

例えば、\(y=x^2\)の逆関数は、\(x =\sqrt {y}\)です。\(y=1\)を満たす\(x\)は\(\pm 1\)と2つあるわけですが、逆関数を考えるときはその片方（正の方）を選んでいます。\(y=x^2\)の定義域を\(0\leq x \)とすることで、逆関数（つまり正の平方根）\(\sqrt {x}\)を定められました。

同じ議論をしましょう。\(y=\tan x\)となる\(x\)は、\(x=0\)だけではありません。\(x=2\pi,-2\pi,\dots\)でも\(\tan x=0\)です。値\(y\)に対して、\(y=f(x)\)となるようなただひとつの\(x\)が定まらなければ、逆関数は存在しません。\(\arctan 0 = \{0,2\pi ,4\pi\}\)のように複数の値を対応させる関係は、関数とは呼ばれないのです。

画像引用：WolpramAlpha

そこで\(\tan x\)の定義域を\(-\frac{\pi}{2}<x <\frac{\pi}{2}\)に制限します。すると、与えられた\(y\)に対して、\(y=\tan x\)となる\(x\)がただひとつ存在する。つまり逆関数が存在するので、それを\(\arctan x\)と書き表すわけです。そのグラフは、\(f(x)=\tan x,-\frac{\pi}{2}<x <\frac{\pi}{2} \)を\(y=x\)について反転させたものになっています。

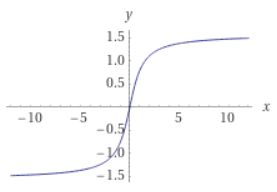
画像引用：WolframAlpha

\(\tan x\)の値域（取りうる値の範囲）は実数全体\(\mathbb{R}\)なので、\(\arctan x\)の定義域はすべての実数\(\mathbb{R}\)となっています。\(\tan x\)の定義域を\(-\frac{\pi}{2}<x <\frac{\pi}{2}\)と制限したので、\(\arctan\)の値域は\(-\frac{\pi}{2}<\arctan x < \frac{\pi}{2}\)です。例えば、\(\arctan(\tan 2\pi)=2\pi\)は誤りです。\(\arctan(\tan 2\pi)=0\)となります。

\(\sin x\)の逆関数\(\arcsin x\)を考えるときにも、同様の注意が必要となります。

\(sin x =0\)となる\(x\)は、\(x =0, n\pi\)とたくさんあります。そこで\(-\frac{\pi}{2}\leq x \leq \frac{\pi}{2}\)と制限すれば、\(0\leq y \leq 1\)なる\(y\)に対して、\(y= \sin x\)を満たす\(x\)がただひとつ存在します。これによって定まる逆関数を、\(\arcsin x\)と表すわけです。

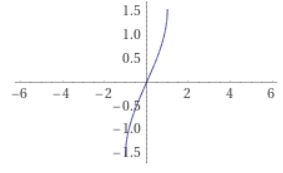
画像引用：WolframAlpha

\(\sin x\)の値域は\(1\leq x \leq 1\)だったので、\(\arcsin \)の定義域は\(1\leq x \leq 1\)です。\(\sin\)の定義域を\(-\frac{\pi}{2}\leq x \leq \frac{\pi}{2}\)に制限して逆関数を考えたので、\(\arcsin\)の値域は\(-\frac{\pi}{2}\leq x \leq \frac{\pi}{2}\)となります。

\(\arccos\)も、\(\cos x\)の定義域を\(0\leq x \leq \pi\)とした関数の逆関数として定義されます。

こうして定義された三角関数の逆関数を、総じて逆三角関数（inverse trigonometric functions）と呼びます。\(\arctan\)はアークタンジェント、逆正接関数、\(\arcsin\)はアークサイン、逆正弦関数、\(\arccos\)はアークコサイン、逆余弦関数。アークarcは弧を意味し、逆三角関数が値として弧長＝角度（ラジアン）を返すことに対応しています。

逆関数\(f^{-1}\)の表記になぞらえて、これらを\(\tan^{-1},\sin^{-1},\cos ^{-1}\)と表記することがありますが、おすすめしません。実数としての逆数\(\frac{1}{\tan x}= (\tan x)^{-1}\)と紛らわしいので。三角関数のべき乗を\(\sin^2 x\)などと表すことは一般的ですが、微妙です。少し手間ですが、\((\sin x)^2\)と書いた方が紛らわしさはなくなります（\(\sin x^2\)と区別できている）。

（三角関数の逆関数が存在することは、厳密には次のようにして示せます。一般に、狭義単調増加な連続関数は、逆関数が存在します。また、微分可能な関数について、狭義単調増加であることと導関数が常に正であることは同値です。つまり、三角関数の微分が適切な定義域で正となることを示せば良い。）

（一般に、関数\(f\)に逆関数が存在することは、\(f\)が全単射であることと同値です。\(f\)が線形写像のときは、逆関数が存在することは可逆であると呼ばれ、その逆関数は逆行列と呼ばれます。）

逆三角関数の微分と応用

逆関数の微分は、次のようになります。（逆三角関数の定義域に注意しましょう。）

\[ \begin{aligned}(\arctan x)^{\prime} = \frac{1}{x^2 +1}\end{aligned} \]

\[ \begin{aligned}(\arcsin x )^{\prime} = \frac{1}{\sqrt{1-x^2}}\end{aligned} \]

\[ \begin{aligned}(\arccos x )^{\prime} = -\frac{1}{\sqrt{1-x^2}} \end{aligned} \]

つまり右辺の原始関数（のひとつ）は、次のように表されるわけです。

\[ \begin{aligned}\int \frac{1}{x^2 +1} dx =\arctan x\end{aligned} \]

\[ \begin{aligned}\int \frac{1}{\sqrt{1-x^2}} dx =\arcsin x\end{aligned} \]

逆三角関数を学ぶ意義のひとつは、このように積分計算に役立つからだと言えます。対数＝逆・指数関数は、\(\int \frac{1}{x} dx = \log |x|\)という積分計算に登場するのと同じ。

一般に、\(f\)の逆関数を\(f^{-1}\)と表すとき、逆関数の微分は\((f^{-1})^{\prime} (x) =\frac{1}{f^{\prime}(f^{-1}(x))}\)となります。（証明略。解析入門の逆関数の章を参照）

\(\arctan x = \theta\)の\(x\)に関する微分は、\((\tan \theta)^{\prime} =\frac{1}{(\cos \theta)^2}=1 +(\tan \theta)^2\)だったので、\(\frac{d\theta}{dx} = \frac{1}{1+(\tan (\arctan x))^2}=\frac{1}{1+x^2}\)です。これは冒頭の積分における計算と同じですね。

次の形の積分は、\(\int \frac{1}{f^{\prime}(f^{-1}(x))} dx = f^{-1}( x)\)と逆関数で表せます。

\(\arcsin x\)の微分を導いて、積分計算に応用してみましょう。

\(\theta =\arcsin x\)と置いて、両辺を\(x\)について微分します。逆関数の定義より、\(-\frac{\pi}{2}\leq \theta \leq \frac{\pi}{2}\)となっていることに注意すれば、\((\sin \theta)^{\prime}= \cos \theta=\sqrt{1- (\sin \theta)^2}\)です。したがって、\(\frac{d\theta}{dx} =\frac{1}{\sqrt{1-(\sin (\arcsin x))^2} }= \frac{1}{\sqrt{1-x^2}}\)が導けました。

例えば、次のような積分が計算できます。

\[ \begin{aligned}\int_0 ^{\frac{1}{2}} \frac{1}{\sqrt{1-x^2}}dx = \arcsin \frac{1}{2} – \arcsin 0 =\frac{\pi}{6}\end{aligned} \]

これは、\(x = \sin \theta\)と置換して計算したことと同じです。

以上、特定の積分の計算に、逆三角関数、その微分が役立っていることを紹介してきました。

高校の微積分では、このような関数の定積分のみを扱い不定積分を出さないことで、逆三角関数の概念を表に出さないようにしています。ただし、逆三角関数を知ることで、俯瞰的な視点から簡単に積分を計算できます。多くの関数の微分を知っていることは、多くの関数の積分を計算できることにつながるので、ぜひ逆三角関数とその微分に親しんでみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。