どうも、木村(@kimu3_slime)です。
今回は、sinc関数と呼ばれる関数を扱い、その積分である正弦積分の近似値を求めてみます。
sinc関数とは何か
sinc関数(シンク関数)は、三角関数を\(1/x\)で割って定義される関数です。
\[ \begin{aligned}\mathrm{sinc}\, x := \frac{\sin x}{x}\end{aligned} \]
\(1/x\)は\(x=0\)で定義されていないので、sinc関数もそうであるように見えるかもしれませんが、問題ありません。
\(\lim _{x\to 0} \frac{\sin x}{x} =1\)となるように三角関数は定義されているので、\(\mathrm{sinc}\, 0:=1\)と定義すれば連続な関数となります。
参考:ラジアン(弧度法)を学ぶのはなぜ? 三角関数の微分を単純化
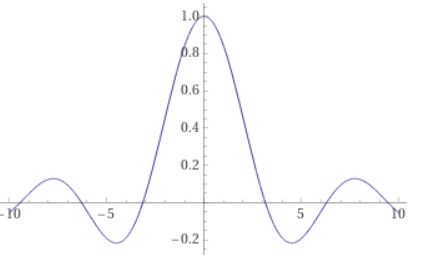
画像引用:WolframAlpha
\(\sin x\)は強さが一定の周期的な波でしたが、\(1/x\)をかけることによって、原点付近では強く、遠方では弱まっていく波になったのが見て取れます。
sinc関数は、例えば光学に現れます。長方形レンズの像の強さの分布は、sinc関数の2乗に比例するようです。(参考:光学第6章 回折と分解能 – 黒田和男)
また、長方形の形をした波:矩形波のフーリエ変換としても、sinc関数は登場します。したがって、電気や音、光といった波を通じて情報を送る、信号理論にも応用されているでしょう。
正弦積分の近似値をテイラー展開で求めてみよう
\(\mathrm{sinc}\, x\)のグラフの面積、すなわち積分には、正弦積分(sine integral)と呼ばれる名前がついています。
\[ \begin{aligned}\mathrm{Si} (x):=\int_0 ^x \mathrm{sinc}\, x dx = \int _0 ^x \frac{\sin x}{x}\end{aligned} \]
無限の範囲\(x\to \infty\)を取った広義積分については、厳密な値が知られています。(複素積分の理論によって計算するのが簡単)
\[ \begin{aligned}\lim_{x\to \infty} \mathrm{Si} (x)=\int_0 ^\infty \mathrm{sinc}\, x dx = \frac{\pi}{2}\end{aligned} \]
しかし有限の値\(x\)に対しては、\(\mathrm{Si}(x)\)を計算するのは大変です。この積分によって定義される関数は、\(x^n,\sin x ,e^x\)といった初等関数で表せないことが知られています。
そこで今回は、\(\mathrm{sinc}\, x\)のテイラー展開によって、正弦積分\(\mathrm{Si}(\pi)\)の近似値を求めてみましょう。\(x=\pi\)は、\(x>0\)で\(\mathrm{sinc}\, x\)が最初に0になる点です。
三角関数\(\sin x\)の\(x=0\)におけるテイラー展開は
\[ \begin{aligned}\sin x = x -\frac{x^3}{6}+ \frac{x^5}{120}- \cos c \frac{x^7}{7!}\end{aligned} \]
なので、
\[ \begin{aligned}\frac{\sin x}{x} = 1 -\frac{x^2}{6}+ \frac{x^4}{120}-\cos c \frac{x^6}{7!}\end{aligned} \]
となります。ただし、\(0<c<x\)です。

画像引用:WolframAlpha
最初の3項で近似して、正弦積分の近似値を求めてみます。
\[ \begin{aligned} \int_0 ^{\pi} \mathrm{sinc}\, x dx & \simeq \int_0 ^{\pi} (1 -\frac{x^2}{6} + \frac{x^4}{120})dx \\ &= [x-\frac{x^3}{18}+ \frac{x^5}{600}]^{\pi}_0 \\ &= \pi-\frac{\pi^3}{18}+ \frac{\pi^5}{600}\\ & \simeq 1.93\end{aligned} \]
となりました。
誤差の大きさを評価してみます。剰余項\(\cos c \frac{x^6}{6!}\)の積分を評価すれば良いです。\(0<x<\pi\)において\(0\leq \cos c \leq 1\)であることに注意して、
\[ \begin{aligned} \int_0 ^{\pi} \cos c \frac{x^6}{6!}dx & \leq \int_0 ^{\pi} 1\cdot\frac{x^6}{7!}dx \\ &=[\frac{x^7}{7\cdot 7!}] _0 ^\pi \\&=\frac{\pi^7}{7\cdot 7!} \\& \leq0.1 \end{aligned} \]
です。
まとめれば、\(\mathrm{Si}(\pi)\simeq 1.93\)で、誤差は\(0.1\)以下であることがわかりました。近似の精度を高くすれば、誤差をより小さくできます。
実際コンピュータ計算によると、近似値は\(1.85\dots\)で、問題なく計算できています。
以上、sinc関数の紹介と、その積分である正弦積分の近似値を、テイラー展開によって求めてきました。
積分によって定義される関数は、原始関数が見つからないときは計算しにくいです。そんなときに、テイラー展開により近似値を求める方法が有効であることが、感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080