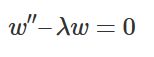どうも、木村(@kimu3_slime)です。
前回、空間1次元、有界区間における熱伝導方程式の解き方を紹介しました。ポイントは、変数分離をして、初期値関数を三角関数の和として表す(フーリエ級数展開)ことでした。
参考:熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)
今回は、全空間(無限領域)における熱方程式のフーリエ変換を使った解き方を紹介します。
フーリエ変換の定義、反転公式
熱方程式は、次の形の偏微分方程式です。
\[ \begin{aligned}\left\{\begin{array}{l}\dfrac{\partial u}{\partial t} &= \Delta u \quad & \text{in } \mathbb{R}^N\times (0,\infty) \\u &= g& \text{on } \mathbb{R}^N\times \{t=0\} \\\end{array}\right.\end{aligned} \]
フーリエ変換(Fourier transformation)は、ある関数を別の変数を持った関数に対応させる積分変換です。熱方程式\(u_t=\Delta u\)の解である未知関数\(u\)をフーリエ変換すると、変換後の関数\(\hat{u}\)はある常微分方程式を満たします。
その常微分方程式は解ける形をしています。そこで得た解を「逆変換」することで、結果として、元の熱方程式の解が得られます。
しかし、いきなり熱方程式から常微分方程式への変換手順を見せても、フーリエ変換そのものの中身がわからなければ意味がわからないでしょう。
そのため、先にフーリエ変換の定義、その性質を紹介します。(先に変換の過程を見てから、戻ってきて読んでも良いかもしれません)
まず、少し唐突ですが、フーリエ変換を次のように定義します。
関数\(u\in L^1 (\mathbb{R}^N)\cap L^2(\mathbb{R}^N)\)に対し、
\[ \begin{aligned}\hat{u}(y):= \frac{1}{(2\pi)^ \frac{N}{2}} \int _{\mathbb{R}^N} u(z) e^{-i y\cdot z} dz \quad y \in \mathbb{R}^N\end{aligned} \]
\[ \begin{aligned}\check{u}(x):= \frac{1}{(2\pi)^ \frac{N}{2}} \int _{\mathbb{R}^N} u(y) e^{i x\cdot y} dy \quad x \in \mathbb{R}^N\end{aligned} \]
\(\hat{u}\)を\(u\)のフーリエ変換(Fourier transform)、\(\breve{u}\)を逆フーリエ変換(inverse Fourier transform)と呼びます。逆フーリエ変換は、共役フーリエ変換とも呼ばれます。
\(L^1 ,L^2\)はルベーグの意味で1乗可積分、2乗可積分関数のなす空間です。詳しくはルベーグ積分の教科書、例えば吉田「ルベーグ積分入門―使うための理論と演習」を参照。
フーリエ変換の定義を、フーリエ級数の場合と比較しながら理解していきましょう。
まず、\(e^{i x\cdot y}\)と虚数を含む式が出てくることについて。フーリエ変換後の世界では、関数は複素数値を持つことを許容しています。
オイラーの公式\(e^ {i\theta} = \cos \theta + i \sin \theta\)によって、三角関数を統一的に扱うために都合の良いものです。
一般に、フーリエ級数展開は
\[ \begin{aligned}u(x)=\frac{a_0}{2} + \sum _{k=1} ^{\infty} a_k \cos kx + \sum _{k=1} ^{\infty} b_k \sin kx\end{aligned} \]
と表されますが、
\[ \begin{aligned}\cos \theta = \frac{1}{2} (e^ {i\theta} + e^{-i \theta})\end{aligned} \]
\[ \begin{aligned}\sin \theta = \frac{1}{2i} (e^ {i\theta} – e^{-i \theta})\end{aligned} \]
を使ってまとめると、複素係数\(c_k\)を使って
\[ \begin{aligned}\sum _{k=-\infty } ^{\infty } c_k e^{ikx}\end{aligned} \]
と表せます。とてもシンプルになりました。
周期\(2\pi\)の関数に対して、係数は次のようになります。
\[ \begin{aligned}c_k = \frac{1}{2\pi } \int _{-\pi} ^{\pi} u(x) e^{-i k x} dx\end{aligned} \]
フーリエ級数展開に対応するのが、フーリエの反転公式(Fourier inversion theorem)です。
ある関数をフーリエ変換し、それを逆変換すると、元に戻る \(u=\check{ (\hat{u})} \) という性質。
これを書き下すと、
\[ \begin{aligned}u(x)= \frac{1}{(2\pi)^ \frac{N}{2}} \int _{\mathbb{R}^N} \hat{u}(y) e^{i x\cdot y} dy\end{aligned} \]
\[ \begin{aligned}\hat{u}(y):= \frac{1}{(2\pi)^ \frac{N}{2}} \int _{\mathbb{R}^N} u(z) e^{-i y\cdot z} dz \end{aligned} \]
となり、級数が積分に\(\sum _k \quad e^{ikx} \leftrightarrow \int \quad e^{ix \cdot y}dy \)、係数は\(c_k \leftrightarrow \hat{u}(y)\)、変数は\(k \leftrightarrow y\)と対応していることがわかります。
フーリエ級数展開は、関数が(有限の)周期を持つときに可能なものでした。フーリエ変換は、それを非周期関数に一般化したものと言えます。
つまり、非周期関数(一般の関数)の「展開」を、周期\(T\)の級数展開で\(T\to \infty\)としたものとして見ます。
このとき、三角級数の\(\cos (\frac{ k}{T} x) ,\sin (\frac{ k}{T} x)\)の隣り合う項の周波数の差は\(\frac{1}{T}\)で、\(T\to \infty\)で\(0\)に近づいていきます。これが離散和(級数)が連続和(積分)になる理由です。
フーリエ変換によって、表現できる関数が多くなった(一般になった)分、基準となる三角関数が連続的で複雑になります。
簡単にまとめます。
フーリエ級数展開、フーリエの反転公式は、ある関数を様々な三角関数の「和」に分けて表すことです。
三角関数は微分の計算で良い性質を持っていて(2回微分で戻ってくる等)、熱方程式の\(\Delta u\)の計算に役立ちます。
周期関数を三角関数の和にするとき、例えば周波数\(k\)の波\(e^{ikx}\)の振幅は\(c_k\)となります。
非周期関数では周波数\(k\)が\(y\)と連続になりますが、周波数\(y\)の波に対応する振幅を求める計算が、\(u\)のフーリエ変換です。一般の関数に対し、どの周波数の成分が、どれくらいの強さで含まれているかが見えやすい世界になります。
そして、周波数-振幅の世界から、元の関数を復元することが、フーリエ逆変換と呼ばれているわけです。
フーリエ変換の性質
フーリエ変換には、計算をする上で様々な良い性質を持っています。その一部を紹介しましょう。
微分のフーリエ変換は、元の関数のフーリエ変換にべき乗をかけたものになります。
\[ \begin{aligned}\widehat{D^\alpha u}(y) = (iy)^{|\alpha|} \hat{u}\end{aligned} \]
ここで、\(\alpha =(\alpha_1,\dots, \alpha_N)\in \mathbb{Z}_{\geq 0} ^N\)は多重指数(multiindex)と呼ばれるもので、
\[ \begin{aligned}D^\alpha u (x):= \dfrac{ \partial ^{|\alpha|} u(x)}{\partial x_1 ^{\alpha_1} \cdots \partial x_N ^{\alpha_N} }\end{aligned} \]
\[ \begin{aligned} |\alpha| := \alpha_1 +\cdots+ \alpha _N\end{aligned} \]
例えば1次元ならば、\(\widehat{D^2 u}(y) =- |y|^2 \hat{u}\)です。2回微分すれば-1が出てくるのは、三角関数の性質ですね。
フーリエ変換同士の積は、畳込みのフーリエ変換となります(畳み込み定理)
\[ \begin{aligned}\hat{u}(y)\hat{v}(y) = \frac {1}{(2\pi)^{\frac{N}{2}}} \widehat{u*v}(y)\end{aligned} \]
ここで、関数\(u,v\)の畳み込み(convolution)、または合成積は、次のように定義される関数です。
\[ \begin{aligned}u*v (x) = \int_{\mathbb{R}^N} u(x-z) v(z )dz\end{aligned} \]
微分に関する法則は、部分積分とリーマン・ルベーグの補題(\(\lim _{|y|\to \infty} \hat{u}(y)=0\))により、畳み込みの定理は、指数関数の計算により証明できます。詳しくは、Evans「Partial Differential Equations 」を参照。
フーリエ変換による熱方程式の解き方
では、フーリエ変換を使って、全空間\(\mathbb{R}^N\)における熱方程式を解いてみましょう。
\[ \begin{aligned}\left\{\begin{array}{l}\dfrac{\partial u}{\partial t} &= \Delta u \quad & \text{in } \mathbb{R}^N\times (0,\infty) \\u &= g& \text{on } \mathbb{R}^N\times \{t=0\} \\\end{array}\right.\end{aligned} \]
方程式を変数\(x\)についてフーリエ変換すると、微分のフーリエ変換の法則により、\(\widehat{\Delta u}= -|y|^2 \hat{u}\)となるので、
\[ \begin{aligned}\left\{\begin{array}{l}\dfrac{\partial \hat{u}}{\partial t} &= -|y|^2 \hat{u} \quad & \text{in } \mathbb{R}^N\times (0,\infty) \\\hat{u} &= \hat{g}& \text{on } \mathbb{R}^N\times \{t=0\} \\\end{array}\right.\end{aligned} \]
これは\(\hat{u}\)の\(t\)に関する常微分方程式で、簡単に解くことができて、
\[ \begin{aligned}\hat {u} = e^{-t|y|^2} \hat{g}\end{aligned} \]
となります。両辺をフーリエ逆変換すれば、フーリエの反転公式と畳込み定理より、
\[ \begin{aligned}u = \frac{1}{(2\pi)^{\frac{N}{2}}} (e^{-t|y|^2})^{\lor} *g\end{aligned} \]
となります。ここで、多重積分によって計算すると
\[\begin{aligned} (e^{-t|y|^2})^{\lor}(x)&=\frac{1}{(2\pi)^{\frac{N}{2}}} \int_{\mathbb{R}^N} e^{i x\cdot y – t|y|^2} dy \\&= \frac{1}{(2\pi)^{\frac{N}{2}}} \prod _{j=1} ^N \int_{\mathbb{R}} e^{i x_j y_j – t{y_j}^2} dy_j \end{aligned}\]
となります。
このとき、右辺はガウス積分に帰着させて計算できます。
\[ \begin{aligned}\int _\mathbb{R} e^{-x^2} dx = \sqrt{\pi} \end{aligned} \]
\[\begin{aligned}\int_ \mathbb{R} e^{iax – bx^2}dx &= \frac{e^{\frac{-a^2}{4b}}} {b^{\frac{1}{2}}} \int_\Gamma e^{-z^2}dz \\&= e^{\frac{-a^2}{4b}} (\frac{\pi}{b}) ^{\frac{1}{2}} \end{aligned}\]
\(z= b^{\frac{1}{2}} x – \frac{a}{2 b^{\frac{1}{2}}} i, a,b\in \mathbb{R}\)と変数変換しました。
\(a=x_j,b=t\)としてさきほどの計算の続きを行えば、
\[\begin{aligned}(e^{-t|y|^2})^{\lor}(x)&= \frac{1}{(2\pi)^{\frac{N}{2}}} \prod _{j=1} ^N \int_{\mathbb{R}} e^{i x_j y_j – t{y_j}^2} dy_j \\&= \frac{1}{(2t)^{\frac{N}{2}}} e^{- \frac{|x|^2}{4t}}\end{aligned}\]
となります。よって、解は
\[\begin{aligned}u(x,t) &= \frac{1}{(2\pi)^{\frac{N}{2}}} (e^{-t|y|^2})^{\lor} *g \\&= \frac{1}{(4\pi t)^{\frac{N}{2}}} \int_{\mathbb{R}^N} e^{-\frac{|x-y|^2}{4t}} g(y)dy\end{aligned}\]
と得られました。
右辺の積分は、ガウス積分に似た積分であり、計算しにくいですね。特定の範囲で\(g=1\)となるときは、誤差関数と呼ばれる特殊関数になります。
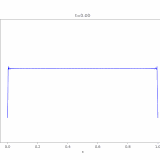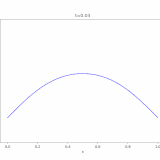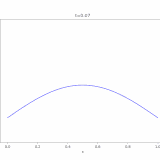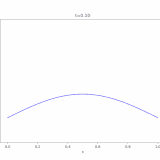
\(N=1\)、初期関数\(g\)を\(-1\leq x \leq 1\)で\(1\)、それ以外で\(0\)という値を取る関数としたとき、解をコンピュータでアニメ化したのが次の図です。
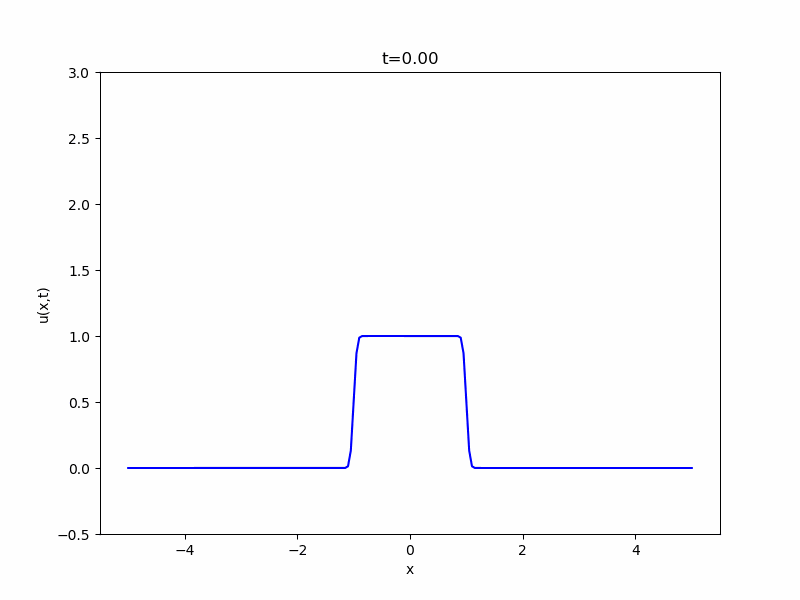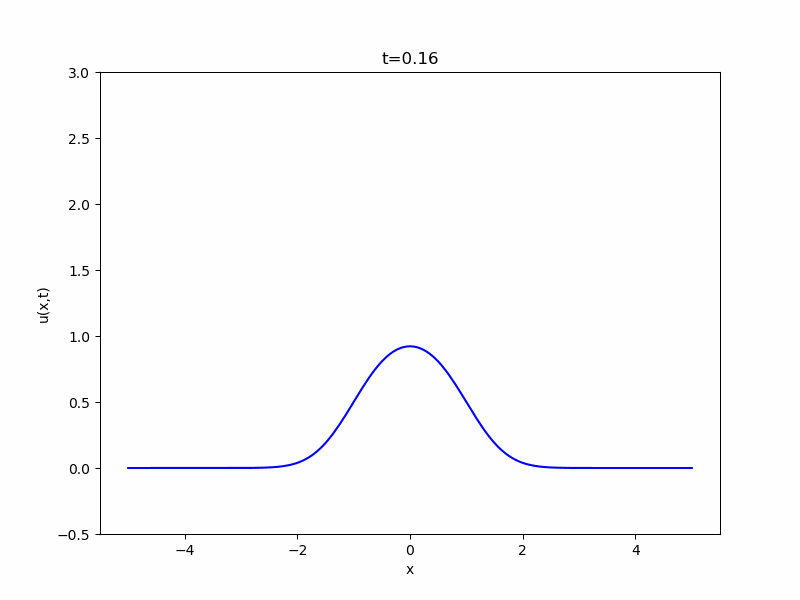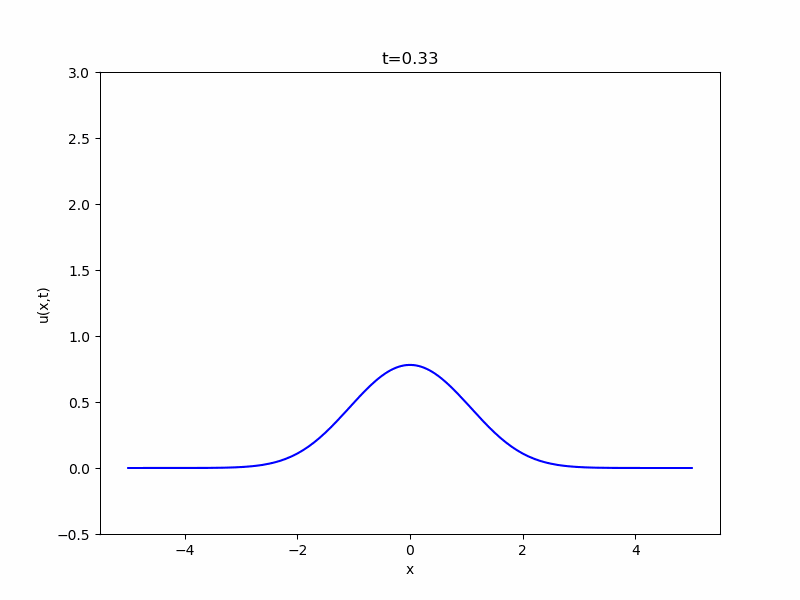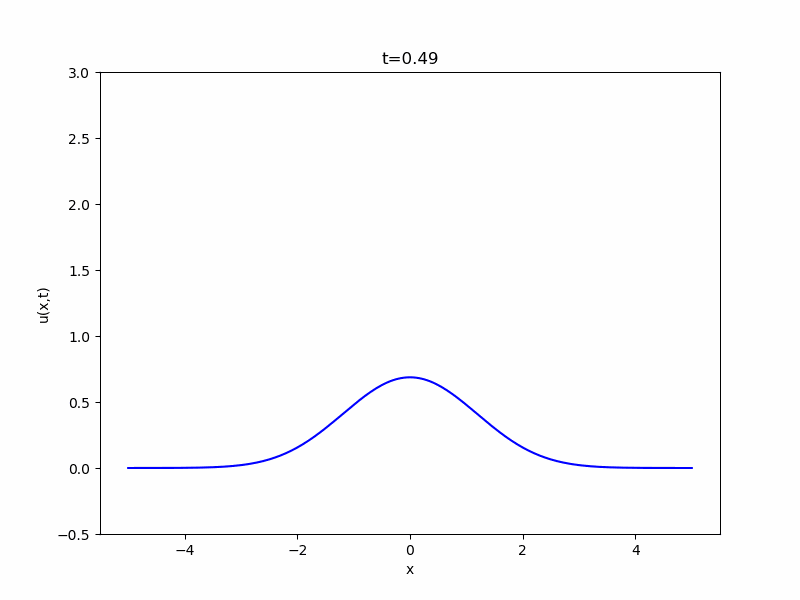
最初は凸の字の形をしていますが、時間が経つにつれ拡散していき、広がって平べったくなっているのがわかります。
ちなみに、ここで
\[ \begin{aligned}K(x,t)= \frac{1}{(4\pi t)^{\frac{N}{2}}} e^{-\frac{|x|^2}{4t}} \end{aligned} \]
とおくと、解は\(K\)と初期関数\(g\)の畳み込みとなっています。
\[ \begin{aligned}u(x,t) = (K* g)(x,t) \end{aligned} \]
この\(K\)は、熱方程式の基本解(fundamental solution)、または熱核(heat kernel)と呼ばれるものです。
(基本解を求めるだけならば、フーリエ変換を使わない方法もあります。)
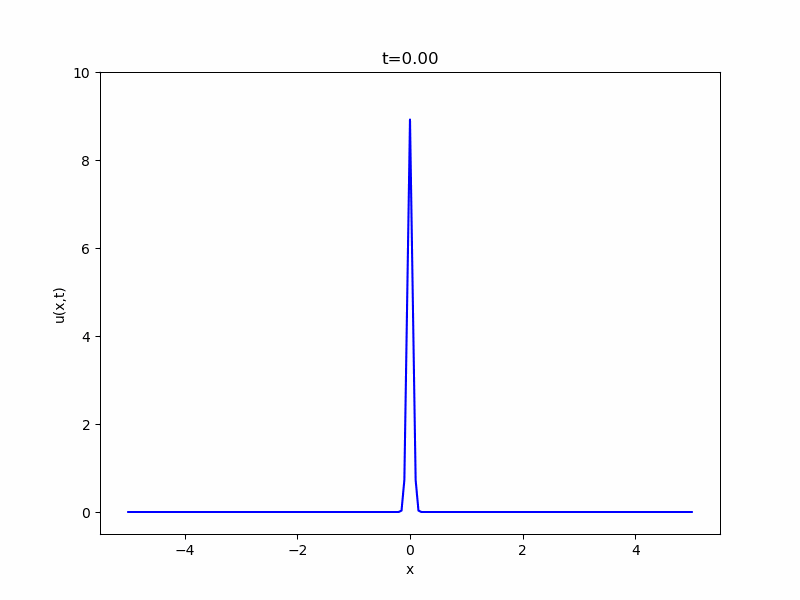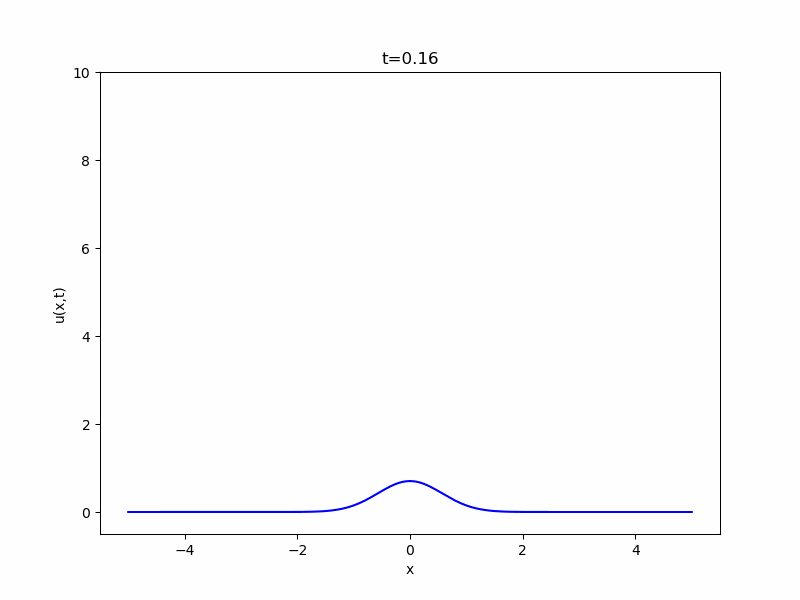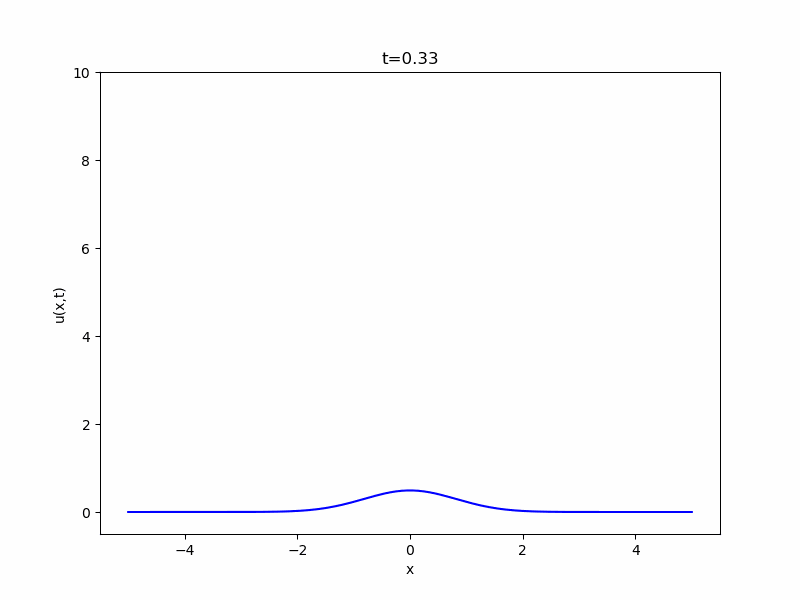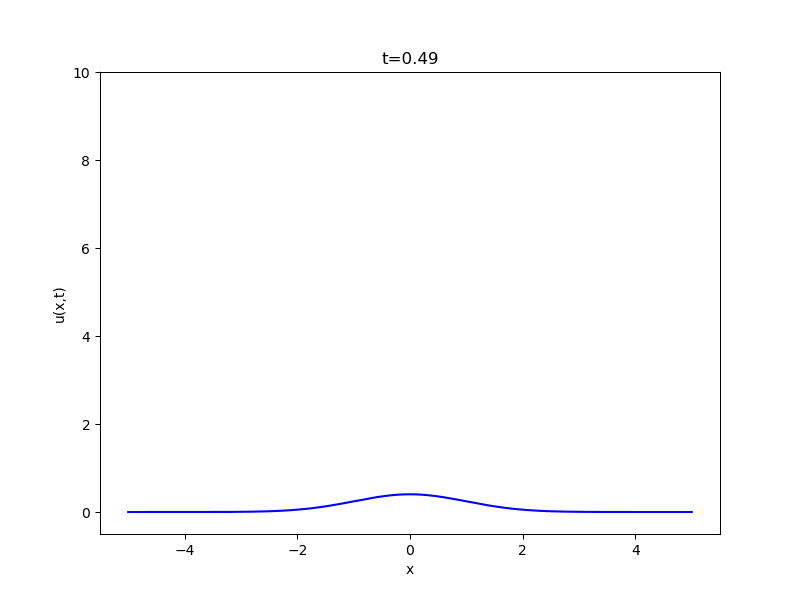
\(t\)が小さいときは原点付近にその値が集中し、時間が経つにつれ空間的に拡散していきます。このような動きと初期関数を組み合わせた(畳み込んだ)のが、一般の熱方程式の解の動きです。
今回は、フーリエ変換によって熱伝導方程式を解く方法を紹介しました。
フーリエ変換すると、指数関数(三角関数)の性質の良さによって\(\Delta u\)から\(x\)微分を取り除き、常微分方程式を取り出せました。
それを解き、フーリエ逆変換を計算すると、熱方程式の一般的な解が基本解と初期値の畳み込みとして表せることがわかりました。
関数の変換によって偏微分方程式を解く方法としては、ラプラス変換(Laplace transform)も有名です。
ただしこうした積分変換による解法が有効なのは、基本的には定数係数の線形な偏微分方程式の場合です。変数係数や非斉次の問題、非線形の方程式では別の方法が必要となります。
また今回紹介したフーリエ変換は、偏微分方程式を解くことだけでなく、コンピュータにおける信号処理や画像処理に応用されていて、離散フーリエ変換(DFT)や高速フーリエ変換(FFT)と呼ばれる手法が生み出されています。
電気や音などあらゆる波動現象を分析するのにフーリエ変換は使えますが、今回の熱方程式の例によって、その威力を感じ取れたのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society
売り上げランキング: 16,244
信号解析のための数学-ラプラス変換,z変換,DFT,フーリエ級数,フーリエ変換-
森北出版
売り上げランキング: 175,330
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)