どうも、木村(@kimu3_slime)です。
空間における熱の広がり方、物質の拡散の仕方は、熱方程式(熱伝導方程式・拡散方程式)という偏微分方程式によって説明されます。
基礎知識と導出はこちら:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、なぜ重積分を学ぶ? 熱伝導方程式の導出を例に
今回は、空間1次元の場合の熱方程式を、変数分離法、フーリエ級数展開によって解く方法を紹介します。
変数分離法によって特殊解を求める
区間\([0,1]\subset \mathbb{R}\)における次のような熱方程式を考えます。
\[ \begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial u}{\partial t} &= &\Delta u \quad & \text{in } (0,1)\times (0,\infty) \\ u &=& 0& \text{on } \{x=0,1\}\times [0,\infty) \\ u &=& g& \text{on } (0,1)\times \{t=0\} \\ \end{array} \right. \end{aligned} \]
ここで、\(\Delta u = \frac{\partial ^2 u}{\partial x^2}\)です。
一般に、熱方程式の一番目の式のみでは解が決まりません。
そこで今回は、\(t=0\)のときの状態\(g\)と、境界での値\(0\)を指定しました。このような問題を、初期値-境界値問題(initial/boundary-value problem)と言います。
一般に、解の境界での値を指定する条件は、ディリクレ境界条件(Dirichlet boundary condition)と呼ばれます。
この方程式の解がどんなものか、予測していきましょう。仮に、解\(u\)が
\[ \begin{aligned}u(x,t)=v(t)w(x)\end{aligned} \]
と変数\(x,t\)が分かれているように表せたとして、関数\(v,w\)が求められるなら、解\(u\)が求められるのではないでしょうか。
このような方法を、変数分離(separation of variables)と言います。
さてこれに従って計算してみましょう。
変数が分離しているので、偏微分が簡単に計算できて、
\[ \begin{aligned} v'(t) w(x) = v(t) \Delta w (x)\end{aligned} \]
となります。この式から、ある定数\(\lambda \)によって\(v'(t)=\lambda v(t), \Delta w(x)=\lambda w(x)\)という式が導けます。やってみましょう。
今、自明でない解\(u\not \equiv 0\)について考えているので、\(v(t_0)w(x_0)\neq 0\)なる\(t_0,x_0\)が存在します。その点で両辺を割ると
\[ \begin{aligned} \frac{v'(t_0)}{v(t_0)} = \frac{ \Delta w (x_0)}{w(x_0)}\end{aligned} \]
です。両辺の値を\(\lambda\)と置きましょう。すると、一方の変数だけを元の式に代入することで
\[ \begin{aligned}v'(t) =\frac{ \Delta w (x_0)}{w(x_0)} v(t)=\lambda v(t)\end{aligned} \]
\[ \begin{aligned}\Delta w (x) =\frac{ v’ (t_0)}{v(t_0)} w(x)=\lambda w(x)\end{aligned} \]
が得られます。一方の変数を定数としてまとめ、変数を分離することができました。
上の方程式は一階の常微分方程式で、その解は \(v = C e^{\lambda t}\)です。
下の方程式は、空間の次元が\(N=1\)のときは、二階の線形常微分方程式となり、
\[ \begin{aligned} w(x) = \left\{ \begin{array}{l} C_1 e^{\sqrt{\lambda} x} + C_2 e^{\sqrt{-\lambda}x} & \lambda>0 \\ C_1 + C_2 x & \lambda =0 \\ C_1 \cos{\sqrt{-\lambda}x } + C_2 \sin {\sqrt{-\lambda}x } & \lambda <0 \end{array} \right. \end{aligned} \]
二階の線形常微分方程式の解き方について:2階線形常微分方程式を学ぶ意味:熱方程式への応用を例に
(\(N\geq2\)だと、常微分方程式とならず、解き方が変わってくる)
\(w\)を境界条件によって絞り込みましょう。
\(w(0)=w(1)=0\)なので、
\[ \begin{aligned} \left\{ \begin{array}{l} C_1+C_2 = C_1 e^{\sqrt{\lambda}} + C_2 e^{-\sqrt{\lambda}} =0 & \lambda>0 \\ C_1 = C_2 =0 & \lambda =0 \\ C_1 = C_1 \cos{\sqrt{-\lambda} } + C_2 \sin {\sqrt{-\lambda} } =0 & \lambda <0 \end{array} \right. \end{aligned} \]
\(\lambda>0\)のときを考える。
\(C_1= -C_2\)なので、\( C_1 e^{\sqrt{\lambda}} -C_1 e^{-\sqrt{\lambda}}=0\)で、\( C_1 e^{ 2\sqrt{\lambda}} =C_1\)。したがって、\(C_1=0\)。
つまり、\(\lambda\geq 0\)のとき、\(C_1 = C_2=0\)となって自明解しか見つからない。
\(\lambda<0\)のときを考える。
\(C_2 \neq 0\)で、\(C_2 \sin \sqrt {-\lambda} =0\)となる\(\lambda\)を求めると、
\[ \begin{aligned}\lambda = – n^2 \pi ^2 ,\quad n \in \mathbb{N}\end{aligned} \]
したがって、\(w(x)= C_2 \sin n\pi x\)となる。
よって、変数分離で求められる境界値問題の特殊解として、
\[ \begin{aligned}u(x,t)=v(t)w(x)=Ce^{- n^2 \pi^2 t} \sin n\pi x\end{aligned} \]
が得られました。
解の形状をイメージしてみてください。\(n=1\)なら、サインカーブの上側の形で、それが時間とともに指数減衰していきます。\(n\)を増やせば波の数(周波数)が増え、指数減衰の速度も速くなります。
変数分離の方法によって、2階の偏微分方程式が、よりシンプルな問題(2つの常微分方程式)に帰着され、それが解くことができました。難しい問題を変形していって、簡単な問題に分割するのは数学の基本的な考え方です。
解を求める:フーリエ級数展開
これで、境界条件を満たすような解を手に入れました。
残りの問題は、初期条件\(u(x,0)=g\)を満たす解を見つけることです。
ここからが、フーリエによるアイデアのポイントです。
フーリエは熱伝導方程式を導出し、それを解くためにフーリエ級数展開と呼ばれる方法を生み出しました。
彼は大胆にも、
任意の関数は、三角関数の和によって表すことができる
と主張しました。仮にこれが正しいとして、議論を進めましょう。
初期値関数\(g\)を三角関数の和\(\sin n\pi x\)によって分解できたとしましょう。すなわち、
\[ \begin{aligned}g (x)= \sum _{n=1} ^\infty c_n \sin n \pi x \end{aligned} \]
です。これを関数\(g\)のフーリエ級数展開(Fourier series expansion)と呼びます。
(一般のフーリエ級数展開は、サインだけでなくコサインの項を含むものです\( b_0+\sum _{n=1} ^\infty b_n \cos n \pi x + \sum _{n=1} ^\infty c_n \sin n \pi x \)。今回は、境界条件\(u(0,t)=u(1,t)=0\)によって、コサインの項が消えています。\(\cos n\pi \cdot 0 = \cos n\pi =1\)なので、係数が\(b_n=0\)でなければならないので。このようなフーリエ展開を、特にフーリエサイン展開と呼びます。)
フーリエ係数(Fourier coefficient)と呼ばれる係数\(c_n\)は、積分によって求められます。三角関数の積の積分計算の性質により、
\[ \begin{aligned} \int _0 ^1 \sin n\pi x \cdot \sin m \pi x dx = \left\{ \begin{array}{l} 0 & n\neq m \\ \frac{1}{2} & n = m \\ \end{array}\right. \end{aligned} \]
という性質(三角関数の\(L^2\)内積による直交性)があるので、
\[ \begin{aligned}c_n = 2 \int _0 ^1 g(x) \sin n\pi x dx\end{aligned} \]
と定まります。
参考:線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
ここで、\(u\)をさきほどの特殊解の重ね合わせと定義します。
\[ \begin{aligned}u(x,t)= \sum _{n=1} ^\infty c_n e^{-n^2 \pi^2 t} \sin n\pi x\end{aligned} \]
熱方程式は線形方程式であるため、特殊解の有限和もまた境界値問題を満たします(解の重ね合わせの原理)。
したがって、\(u\)は境界値問題を満たします。(数学的に厳密に言えば、この級数の一様収束性、微分可能性、方程式を満たしていることをチェックする必要があります)
また、\(u(x,0)=\sum _{n=1} ^\infty c_n \sin n \pi x = g(x)\)で、初期値問題を満たします。
よって、\(u\)は熱方程式の初期値・境界値問題の解です。
\(g(x)=1\)として、この解を視覚化してみましょう。
フーリエ係数を求めると、\(n\)が奇数のとき
\[\begin{aligned} c_n &= 2 \int _0 ^1 1\cdot \sin n\pi x dx \\ &= 2[\frac{-1}{n \pi} \cos(n\pi x) ]^1 _0 \\ &= \frac{4}{n \pi}\end{aligned} \]
となります(\(n\)が偶数なら0となって消える)。したがって、
\[\begin{aligned} u(x,t) &= \frac{4}{\pi} e^{-\pi^2 t} \sin \pi x + \frac{4}{3\pi} e^{-3^2 \pi^2 t} \sin 3 \pi x \\ &+ \frac{4}{5\pi} e^{-5^2 \pi^2 t} \sin 5\pi x +\cdots \end{aligned} \]
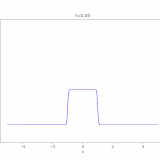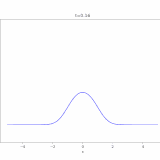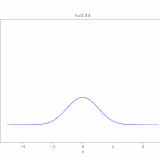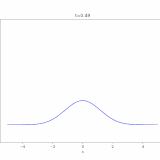
で、これをコンピュータでアニメ化したのが次の画像です。(およそ1000次の項まで)

最初は初期条件は\(g(x)=1\)ですが、境界での値は\(0\)と指定しているので、境界付近の値は一瞬で0に近づいています。一方、中央付近には熱(や化学物質)が残っていますが、それも拡散の効果によって、だんだんと0へ減衰していくのがわかりますね。
解の形状において、\(\sin 3 \pi x ,\sin 5 \pi x \)といった高次の成分は最初は影響がありますが、時間による減衰が強く、後半はほぼ\(\sin \pi x\)の形に支配されています。
ちなみに、1次元の波動方程式
\[ \begin{aligned}\frac{\partial^2 u}{\partial t^2} =\Delta u \end{aligned} \]
も、変数分離とフーリエ級数展開の方法で同様に解くことができます。
2次元以上の場合
今回は1次元でしたが、\(N\geq2\)でも有界領域なら
\[ \begin{aligned}u(x,t)= \sum _{n=1} ^\infty c_n e^{-\lambda_n t} w_n\end{aligned} \]
という形で解を求められます。
ここで\(w_n\)は
\[ \begin{aligned} – \Delta w = \lambda w\end{aligned} \]
の解です。これを固有値問題、解を固有関数と言います。
線形代数では(有限次元の)ベクトルに行列を作用させた問題でしたが、ここでは関数に作用素\(-\Delta\)を作用させています。
このような問題を捉える枠組みが、関数解析(functional analysis)です。
\(-\Delta\)の固有値は無限にあり、すべて正です。さらに、関数列\(\{w_n\}_{n=1}^ \infty\)は、(ルベーグの意味で)2乗可積分関数のなす空間\(L^2\)の正規直交基底であるように取れます。
このような基底があるから、任意の関数が基底の和として表せたわけです。
詳しくは、Evans「Partial Differential Equations」や黒田「関数解析」を参照。
フーリエの発想が生み出したもの:フーリエ解析
これで形式的には解が求められたわけですが、疑わしいのが、フーリエ級数展開の正当性です。
本当に、任意の関数は三角関数の和として展開できるのでしょうか? 係数を定める積分は有限値として定まるのでしょうか?
今回のケースでは、\(g\)が連続関数であるか、あるいは\(g\)が不連続であっても(ルベーグの意味で)2乗可積分\(g \in L^2 \)なら正当化されることが、現在では知られています。
例えば、吉田「ルベーグ積分入門―使うための理論と演習」を参照。
これを厳密に正しいか調べるため、フーリエ級数の理論が発展し、その総称としてフーリエ解析(Fourier analysis)と呼ばれる分野が生まれてきました。
フーリエ解析は、現在の大学数学、理工系の授業で1科目として教えられるほど重要なものです。
今回は有界な区間を考えたため、初期関数は三角級数で表せました。しかし、一般に全空間\(\mathbb{R}^N\)上の関数は離散的な和として表せません。しかし、連続的な和、すなわち積分によって表すことができ、これはフーリエ変換(Fourier transform)として知られています。
また、フーリエの主張は、「連続とはどういうことか」「級数が収束するとはどういうことか」といった問題をきちんと議論する方向へ、解析学の厳密化のきっかけのひとつとなりました。
フーリエ級数展開は、例えば区分的になめらかな関数(不連続点が有限個で、不連続点で無限の値をとらないなめらかな関数)でも可能なことが知られていきます。
集合論の父・カントールは、三角級数展開の一意性を調べ、「一意展開できる点の集合」を調べることで解決しました。その後彼は、有理数の集合の可算性、実数の非可算性を残し、集合論のベースを生み出していきました。
参考:三角級数の一意性 – fujidig、カントール,ゲオルク 、「集合と位相をなぜ学ぶのか」レビュー
フーリエの問題提起は、理工学全般、特に数学においても、大きな影響を与えたと言えます。
熱方程式の解法のひとつとしてのフーリエ級数展開、そしてフーリエ解析のモチベーションとしては熱方程式があったことが、伝えられていたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society
売り上げランキング: 33,117