どうも、木村(@kimu3_slime)です。
拡散方程式(かくさんほうていしき)、というものを紹介したいと思います。
身近な例として、花粉をイメージしてみましょう。花粉症の方は、花粉の時期大変な思いをしているのではないでしょうか。
花粉の広がり方、その日どのくらい花粉が飛んでいるかを知ることができたら、対策のしようがありますよね。
花粉症と拡散
実際に、川島茂人「スギ花粉拡散過程のモデル化 – JSTAGE」という論文があります。
拡散方程式を使って、花粉の広がり方をシミュレーションで予測した研究ですね。下図の「移流&拡散過程」の説明に、拡散方程式を使っています。
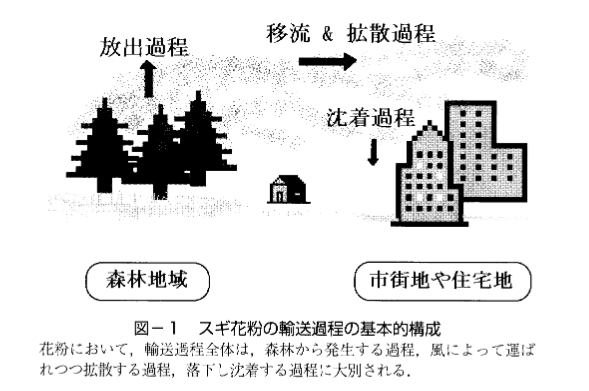
空気中での花粉物質の広がり方には規則性があるので、それをモデル化すれば花粉の動き予測できるのではないか、というものです。
日本気象協会は、1990年から毎年花粉の飛散予測を出しています。実際の計測や過去のデータにもとづいた予測もあるでしょうが、拡散を意識した予測もきっと含まれているのではないでしょうか。
拡散とは
拡散(diffusion)とは、自発的に粒子が広がる現象のことです。
空気や水をかき混ぜなくても、物質の濃度が均質となるように広がることを指しています。
例えば、次の動画を見てみてください。インクが水中で広がっていく様子がわかります。温かい水の方が拡散のスピードが速いですね。

また、最初インクが落下しているのは、純粋に拡散のみが起こっているわけではないからです。これには物質がそのまま動いている、移流(advection)という現象が働いています。
拡散の例は他にもあります。おならのガスは、放出された直後は一時的に匂いますよね(笑)。しかしすぐににおいがなくなります。これは単に鼻が慣れただけではなく、ガスが拡散したからです。空間内に薄く広がったから、臭わなくなったということです。
「大気中の物質拡散入門」というPDFの文章では、原子力発電所からの放射性物質の拡散を例として拡散現象を一般の人向けに紹介しています。Q&A形式で数式もなく、とても読みやすいので、ぜひ読んでみてください。
拡散方程式とは
拡散現象を説明する数式、拡散方程式(diffusion equation)は、次のような偏微分方程式(微分方程式の一種)です。
\[ \begin{aligned}\frac{\partial u }{\partial t}= \Delta u\end{aligned} \]
\(u(x,t)\)は時間\(t\)と空間\(x\)の関数で、物質の濃度(熱で言えば温度)。\(\frac{\partial u }{\partial t}\)は濃度の時間変化率で、時間項と呼ばれ、\(\Delta u\)は拡散を説明する項で、拡散項と呼ばれます。
つまり、物質が拡散するように(濃いところから薄いところへ動くように)広がっていきますよ、というのが拡散方程式です。
熱が伝わる様子も拡散と同じで、拡散方程式は熱方程式(heat equation)とも呼ばれます。
YouTubeでシミュレーション動画を見れば、濃いところから薄いところへ広がり均質になっていくようすがわかるかと思います。
さきほどの花粉やインクの例がそうでしたが、水や空気中の拡散では、拡散と同時に移流が起こります。
これを考慮した式が、移流拡散方程式(advection-diffusion equation)です。
\[ \begin{aligned}\frac{\partial u }{\partial t}= \Delta u – a \cdot\nabla u\end{aligned} \]
\(a \cdot\nabla u\)は空気や水の流れによって物質が動くようすを説明する項で、移流項と呼ばれます。
ちなみに、拡散方程式に(化学反応などをイメージした)反応項を加えると、反応拡散方程式となります。
参考:生き物の模様は数式で決まる? チューリング・パターンとは
花粉や放射性物質、ガスから熱伝導まで、ものが広がるという普遍的な現象を扱っているのが拡散方程式です。
大学数学の世界では、偏微分方程式の最もシンプルな例となる方程式です。別の記事でもこれを掘り下げていくので、お楽しみに。
木村すらいむ(@kimu3_slime)でした。ではでは。