どうも、木村(@kimu3_slime)です。
大学数学の各分野、一般的なロードマップを紹介したいと思います。
東京大学数学科のカリキュラムを参考に、自分なりに図を作りました。
このマップに合わせて入門書を紹介しています:「趣味の大学数学」おすすめ入門書籍・教科書・参考文献
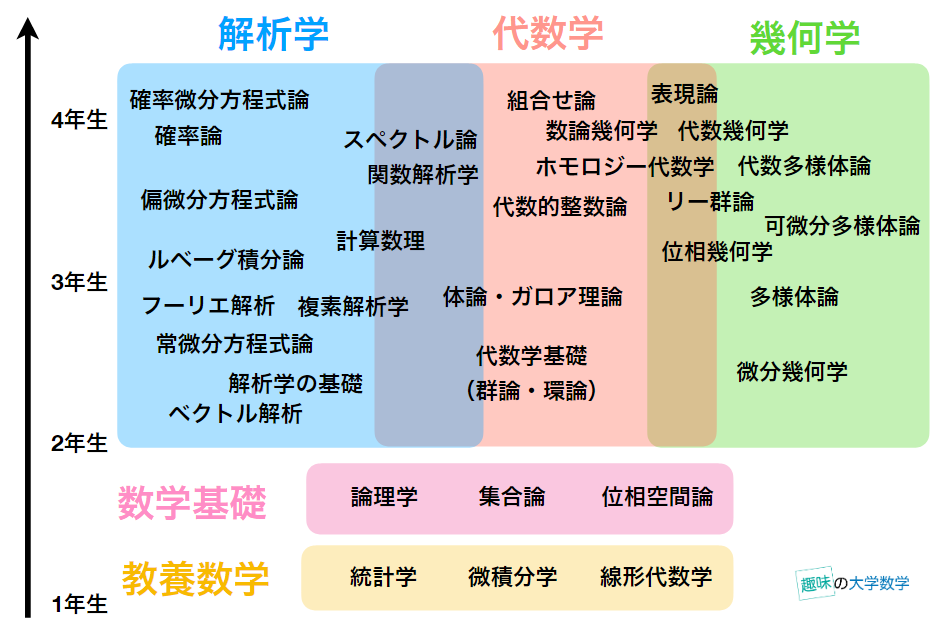
この画像の分野名をクリックすれば、その分野のまとめ記事へ飛びます(一部分のみ対応)。
教養数学
微積分学、線形代数学は、大学で数学をする人はもちろん、自然科学や工学、社会科学や人文科学を学ぶすべての人が身につけて損はない数学です。高校数学から大学数学への接続をするきっかけとなります。
統計学は、特に数学以外への応用に役立つ分野です。ただし、数学の(諸分野の)基礎としての役割は、微積分や線形代数に比べると小さいでしょう。
数学基礎
論理学は、通常数学科のカリキュラムに明示されていませんが、集合論や教養数学で教えられるので明示しておきました。論理学は数学的な考え方の基礎となる考え方で、数学書を読むとき、その論理展開や証明を追うために使います。
集合論、位相空間論は、大学数学の基礎です。のちに紹介する代数学、幾何学、代数学のどの分野でも、集合論・位相空間論の言葉を使います。
僕はこの分野に触れて、はじめて大学の数学がわかったような気がします。
代数学、幾何学、解析学
代数学、幾何学、解析学は、大学数学の3大分野として知られています。
代数学は、整数や方程式をより一般化したものや、物事の対称性を調べる分野。
幾何学は、図形や空間の性質を調べる分野。
解析学は、微分・積分をツールとして関数の性質を調べる分野。
数学専門の人同士が専門を尋ねるときに、この3大分野からまず答えることが多いです。「専門は?」「代数です(特に代数幾何)」といったように。「解析の人なんだ」という言い方もしますね。
また、数学基礎論(ロジック)、計算機数学(情報数学)、物理数学、応用数学などは3大分野と呼ばれていませんが、重要な分野です。
現状では、当サイトは以下の分野を扱っています(分野によって充実具合はバラバラです)。
代数学:抽象代数学(群・環・体)、数論
幾何学:
解析学:微分方程式論、力学系理論、測度論・ルベーグ積分論、確率論
ここで述べたような分野分けは大雑把なもので、問題そのものに分野はありません。整理のために便宜的に呼ばれるに過ぎません。それぞれの分野は相互に関わっているので、いくつかの分野を組み合わせて学ぶのは自然なことです。
例えば、解析的整数論では代数的な対象(整数)を解析的手法(複素解析)で、代数的トポロジーでは幾何学的対象(位相不変な図形)を代数的手法(群論)で分析します。また、力学系理論では解析的な対象(発展方程式)の幾何学的な側面を調べます。
数学は基本的に積み上げ式の学問で、間をすっ飛ばすことはできません。興味ある分野の本を手に取ってみたとき、その本では紹介されていない馴染みのない用語があったら、より基本的な分野の本に戻って勉強していきましょう。それが最短の道です。
高校卒業後に大学数学を学びたいなら、まず数学基礎である集合論・位相空間論を学び、その後好きな3大分野を学んでいけば良いかと思います。
いきなり数学の一般論だとモチベーションが湧かないかもしれないので、難しそうだが気になる分野を探してみて、そこにたどり着く基礎を逆算してみるのも良いでしょう。
上で紹介した図を見ると、分野の数がめちゃくちゃ多いですよね。その全てを順番に学ばなければならない、というわけでもありません。
「趣味の大学数学」では、まず最初に、(僕の専門であった)微分方程式論にたどりつくための記事を提供していきたいと思っています。
大学数学を独学したい方の向けの記事を書きました。
研究分野
ウェブでの論文公開に定評あるサイトarXiv(アーカイヴ)を参考に、数学の主要な研究分野名を紹介します。
- 代数幾何(Algebraic Geometry)
- 代数的トポロジー(代数的位相幾何)(Algebraic Topology)
- 偏微分方程式の解析(Analysis of PDEs)
- 圏論(Category Theory)
- 古典的解析と常微分方程式(Classical Analysis and ODEs)
- 組合せ論(Combinatorics)
- 可換代数(Commutative Algebra)
- 複素変数(Complex Variables)
- 微分幾何(Differential Geometry)
- 力学系(Dynamical Systems)
- 関数解析(Functional Analysis)
- 一般数学(General Mathematics)
- 一般トポロジー(General Topology)
- 幾何学的トポロジー(Geometric Topology)
- 群論(Group Theory)
- 歴史と概観(History and Overview)
- 情報理論(Information Theory)
- K-理論とホモロジー(K-Theory and Homology)
- ロジック(論理)(Logic)
- 数理物理(Mathematical Physics)
- 計量幾何(Metric Geometry)
- 数論(Number Theory)
- 数値解析(Numerical Analysis)
- 作用素代数(Operator Algebras)
- 最適化と制御(Optimization and Control)
- 確率(Probability)
- 量子代数(Quantum Algebra)
- 表現論(Representation Theory)
- 環と代数(Rings and Algebras)
- スペクトル理論(Spectral Theory)
- 統計理論(Statistics Theory)
- シンプレクティック幾何(Symplectic Geometry)
日本学術会議の数理科学委員会による「報告 数理科学分野の展望」というPDFには、これらの分野における研究の概略、発展、今後の展望が書かれています。日本における数学の発展が、数学を専門としない人でも(比較的)読みやすくまとまっているかと。
大学数学の歴史
人類が2000年以上かけて積み上げてきた数学の歴史を見ることで、大学数学のカリキュラムの位置づけがより明確になるでしょう。
およそ、小学校の算数はギリシャ数学(紀元前/2000年以上前)まで、中学校の数学はアラビア数学(700-1500年)まで、高校の数学はヨーロッパ数学の誕生(1600年)までに成立した内容が教えられています。
一方、大学の学部で教えられる教養数学(微積分、線形代数、統計学)は、およそ1900年までの数学です。高校-大学の300年のギャップは大きいので(300年といっても積み重ねの内容が濃い)、つまづいたら歴史を調べてみると良いでしょう。
数学科の学部(2-3年)で教えられるのは、およそ1800-1950年あたりの数学までです。その先の新しい数学は、各自、研究したいものを、自ら学ぶことになるでしょう。
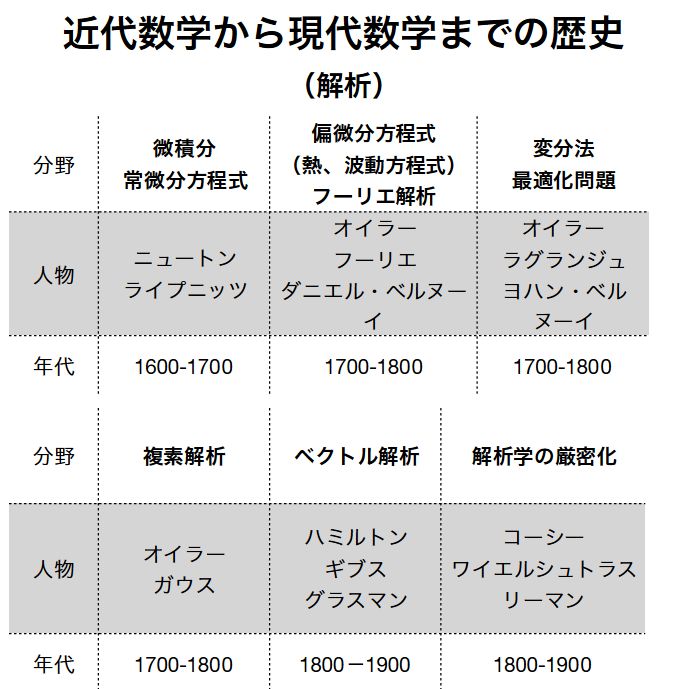

参考:厳密さ・証明が現代数学で要求されるのはなぜ? 近代数学の歴史をたどる
応用数学のロードマップ
これまで紹介してきた数学は、どちらかというと純粋数学と呼ばれる分野です。それを諸科学に役立てる分野は、応用数学と呼ばれます。
応用数学の具体例としては、組合せ論、コンピュータサイエンス、統計・データサイエンス、物理応用数学、経済・ファイナンスなどがあります。
MITの「Math Major Roadmaps」を参考に、応用数学のロードマップを作りました。

中心の4分野「微分方程式、線形代数、確率論、統計学」は、応用数学のどの分野でも必修とされる数学です。真ん中から勉強を始め、外側いずれかの興味ある分野へ進んでいくと良いでしょう。
また、純粋数学とその応用との対応図を作ってみました。数学がこれだけ多くの分野と関連し活用されているのだな、と感じ取ってもらえれば。

ただし、実際にここで書かれた応用分野を学びたいなら、数学ではなく、その分野の教科書を手にとったほうが良いです。あくまで活用が目的なら、数学は必要になった分だけやれば良いので。もし数学そのものを知りたいなら、数学をしましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう