どうも、木村(@kimu3_slime)です。
大学1年の微積分学では、多変数関数の積分、つまり重積分を学ぶかと思います。
重積分の定義や計算手法を学ぶ前に、「なぜ重積分をするのか?」を知りたいですよね(僕は知りたいです笑)。
というわけで、今回は熱伝導方程式の導出を例に、重積分がどのように登場するかを紹介します。(式の意味は全部わからなくて大丈夫!)
先に偏微分の話を知っておくと読みやすいです:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に
熱伝導方程式とは
熱伝導方程式とは、空間に熱が伝わっていくようすを説明する方程式です。
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u\end{aligned} \]
未知関数\(u(x,t)\)は、温度を表す関数です。左辺は時間変化を表す時間項、右辺は熱の拡散を表す拡散項と呼ばれます。
この方程式は、細かい物質の拡散を説明できるため、拡散方程式とも呼ばれます。
このサイトでもすでに何度か紹介しました:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、花粉の広がりを数式で予測する、拡散方程式とは
なぜ、熱方程式はこのような形をしているのでしょうか?
今回は、「熱は熱いところから冷たいところへ流れる」というフーリエの法則から、重積分を使って熱方程式を導いてみたいと思います。
1次元での熱伝導方程式の導出
いきなり重積分を扱うのは難しいので、まずは空間1次元の場合を考えてみましょう。細い針金がイメージです。
針金の外部とは熱のやりとりをしない状況、針金の内部での熱の動きを考えます。内部を区間\(I=(a,b)\)としましょう。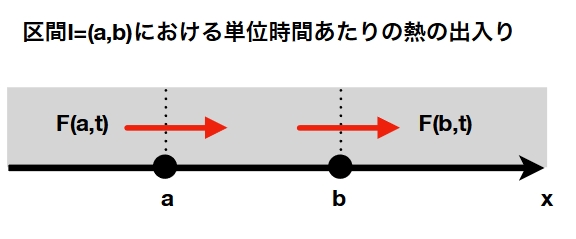
区間の境界における熱のやりとりは、フーリエの法則によって説明されます。
熱の流れ、単位時間に単位面積を流れる熱量を、流束(フラックス、flux)と呼びます(単位は\(\mathrm{J/m\cdot s}\))。
フーリエの法則は、流束\(F(x,t)\)が温度勾配に比例するという法則です。比例定数\(k>0\)は熱伝導率と呼ばれます。
\[ \begin{aligned}F(x,t)=-k\frac{\partial u(x,t)}{\partial x}\end{aligned} \]
単位時間あたりの熱の出入りの合計は
\[ \begin{aligned}F(a,t)-F(b,t)\end{aligned} \]
です。一方で、区間\(I\)に蓄えられている熱量を計算すると
\[ \begin{aligned}J(t)=C\int _a ^b u(x,t)dx\end{aligned} \]
です。ここで\(C>0\)は熱容量と呼ばれる、針金の材質や太さに依存した定数です。(高校物理では\(Q=C\Delta T\)と書かれる式ですね。)
そしてその時間あたりの変化は、\(t\)に関する微分をすれば
\[ \begin{aligned} \frac{dJ(t)}{dt} &= C\frac{d}{dt}(\int _a ^b u(x,t)dx) \\ &= C\int _a ^b \frac{\partial u(x,t)}{\partial t}dx\end{aligned} \]
となります(微分と積分の順序交換)。
熱量保存の法則により、蓄えられている熱量の時間変化は、出入りする熱量の時間変化に等しいです。つまり、
\[ \begin{aligned}\frac{dJ(t)}{dt} = F(a,t)-F(b,t)\end{aligned} \]
これを整理すると
\[ \begin{aligned} C\int _a ^b \frac{\partial u(x,t)}{\partial t}dx &= -k\frac{\partial u(a,t)}{\partial x}-k\frac{\partial u(b,t)}{\partial x} \\ &= k\int^b _a \frac{\partial ^2u(x,t)}{\partial x^2}dx \end{aligned} \]
となります(微積分学の基本定理によって、境界の情報が積分で表せる)。
この等式が区間\(I=(a,b)\)の選び方によらずに成立するためには、積分の中身が常に等しくなければなりません。つまり、
\[ \begin{aligned}C\frac{\partial u(x,t)}{\partial t}=k \frac{\partial ^2 u(x,t)}{\partial x^2}\end{aligned} \]
\(t\mapsto Ct,x\mapsto\sqrt {k}x\)と変数変換し、\(\frac{\partial ^2 u}{\partial x^2}=\Delta u\)と書き直せば、
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u\end{aligned} \]
熱方程式が得られました。
多次元での熱伝導方程式の導出
さて、1次元での議論を、2次元、3次元、多次元\(N\)次元での議論に展開してみましょう。ここで重積分が登場します。
領域\(V\subset \mathbb{R}^N\)における熱の出入りを考えてみましょう。\(x=(x_1,\dots,x_N)\in \mathbb{R}^N\)と表されます。
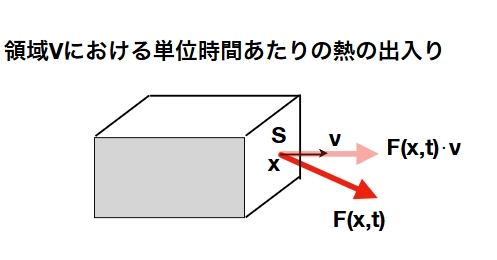
領域\(V\)に蓄えられている熱量は、\(u(x,t)\)の総和に熱容量\(C\)をかけたものです。これが重積分を使って
\[ \begin{aligned}J(t)=C\int_V u(x,t)dx\end{aligned} \]
と表せます。積分区間\(I\)が積分範囲\(V\)に変わっただけですね。その時間変化は、さきほどと同様に
\[ \begin{aligned}\frac{dJ(t)}{dt}= C\int _a ^b \frac{\partial u(x,t)}{\partial t}dx\end{aligned} \]
です。
境界における熱の出入りを考えましょう。流束は、熱の流れる方向、量によって決まるベクトルとなります。そしてフーリエの法則により
\[ \begin{aligned}F(x,t)=-k\nabla u\end{aligned} \]
と与えられます。ここで\(\nabla\)(ナブラ)は勾配作用素と呼ばれ
\[ \begin{aligned}\nabla u = (\frac{\partial u}{\partial x_1},\dots,\frac{\partial u}{\partial x_N})^T \end{aligned} \]
です。
境界からの単位時間あたりの熱の出入りを計算しましょう。さきほどは\(F(a,t)-F(b,t)\)とシンプルでしたが、もう少し複雑になります。
\(V\)の境界\(\partial V\)を通しての熱の出入りは、\(F\cdot \nu\)の\(\partial V\)上の積分によって与えられます。
ここで\(\nu\)は\(\partial V\)の単位法線ベクトル(境界面に対して垂直な大きさ1のベクトル)です。単に\(F\)でなく\(F\cdot \nu\)を考えるのは、境界面に垂直な方向の流束の影響のみを考えたいからですね。
したがって、熱の出入りは
\[ \begin{aligned}\int_{\partial V} F\cdot \nu dS =k \int_{\partial V} \nabla u(x,t)\cdot \nu dS\end{aligned} \]
となります(正負の符号に注意、流束は熱が領域に入る方向を基準としている)。熱量保存の法則により、
\[ \begin{aligned} C\int _a ^b \frac{\partial u(x,t)}{\partial t}dx =-k \int_{\partial V} \nabla u(x,t)\cdot \nu dS \end{aligned} \]
となるわけですが、右辺にガウスの定理と呼ばれる定理をあてはめると
\[ \begin{aligned} -k \int_{\partial V} \nabla u(x,t)\cdot \nu dS &= -k \int_V \mathrm{div}( \nabla u) dx \\ & -k \int_V \Delta udx\end{aligned} \]
となるので、
\[ \begin{aligned} C\int _V \frac{\partial u(x,t)}{\partial t}dx =-k \int_V \Delta udx\end{aligned} \]
これが領域\(V\)の選び方によらず常に成立しているためには、積分する関数が常に等しくなければならない。よって、1次元のときと同様の議論で、
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u\end{aligned} \]
が得られました。
なぜ重積分を学ぶのか。
熱伝導方程式の導出を例として考えればわかりやすいです。ある領域における熱の総量や出入りを考えるときに、そこで熱量という関数の積分を考える必要があるからです。
今回は、微分によって表されるフーリエの法則と熱量保存の法則、重積分の計算によって、熱方程式を導いてみました。
導出の後半では、ガウスの定理を使いました。これは大学1年の微積分学で習う重要な定理のひとつです。
\[ \begin{aligned} \int_{\partial V} \nabla F\cdot \nu dS = \int_V \mathrm{div}F dx \end{aligned} \]
境界における積分は内部における発散(divergence)の積分として表せることから、発散定理とも呼ばれます。
ガウスの定理は、じつは1次元のときの微積分学の基本定理の一般化です。2次元のときは、グリーンの定理とも呼ばれます。
\[ \begin{aligned} [F(x)]^b _a = \int_a ^b \frac{dF}{dx} dx \end{aligned} \]
今回の話を知っておけば、重積分の定義や計算手法、発散定理の話も理解しやすくなるかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響