どうも、木村(@kimu3_slime)です。
統計学には、調べたい対象全体のデータを取ることができなくても、その一部をサンプルとしてランダムに選ぶことにより、元の対象全体(母集団)の性質を調べる方法があります(推測統計学)。
その入門の話をしていきたいのですが、「ランダムに選ぶ」部分から確率論の考え方・用語が入ってきて、少しわかりにくくなる印象です。
今回は、二項分布や正規分布に見られる用語「分布」が何を意味しているのかについて、整理していきます。
頻度分布、統計的推測
統計学では、調べたい現象に対し、それを数量化したデータを大量に集めることで、現象の傾向を探ろうとします。そのデータを、一定の仕組みの繰り返しによって得られたもの、つまり試行(trial)や実験(experiment)によって得られたと捉えます。
例えば、(表裏が平等に出る)コインを100回投げるという試行を考えます。100回中46回出た、45回出た、54回出た……試行を重ねれば、データが溜まってゆきます。
このとき、どういう結果がどのくらいの割合で起こっているのか? これを調べるのにわかりやすいのが、結果の回数(頻度 frequency)を可視化する分布の考え方です。
頻度分布(frequency distribution)は、度数分布、またはヒストグラムとも呼ばれます。それは、起こった結果をクラス(階級)と呼ばれる分で分類し、各クラスごとの頻度をグラフとして表したものです。
例えば次の図は、コインを100回投げるという試行を10回行ったときの頻度分布です。
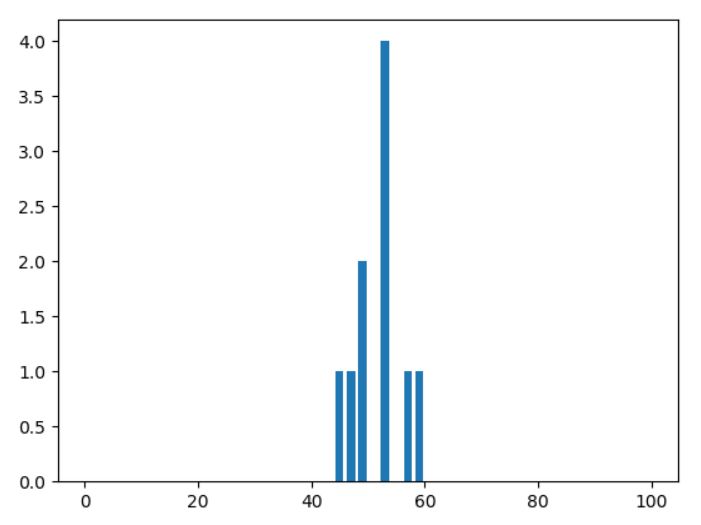
試行を100回、1000回と増やすと、頻度の分布には何か規則性があるように見えてきますね。
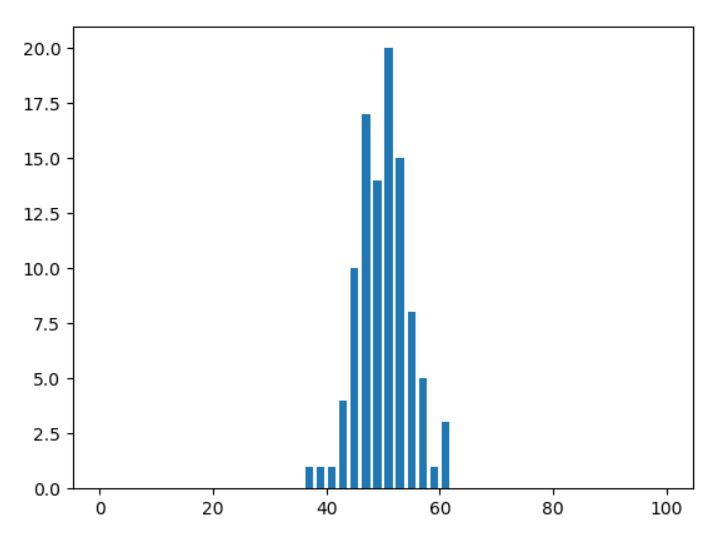
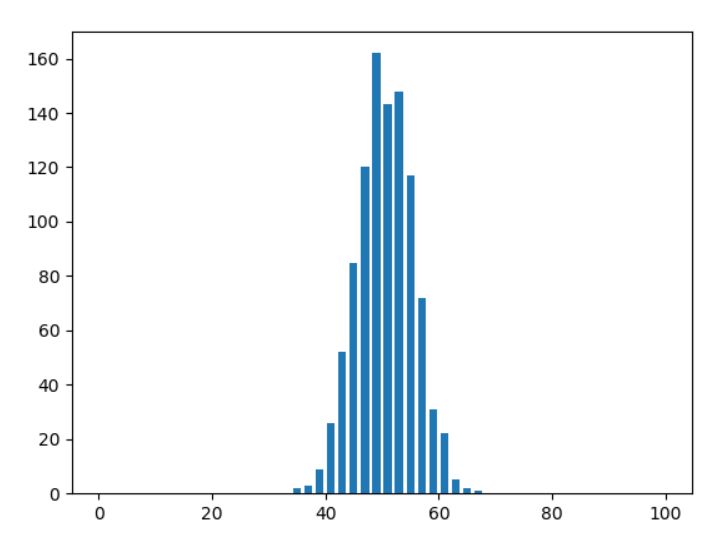
例えば、100回中50回表が出るような試行が最も多そうだ……ということが見てわかります。
しかし縦軸がこのままだと、全体に対してどのくらいの割合で特定の結果が起こるのかがわかりにくいです。
得られた頻度(絶対頻度)を全体の試行回数で割ることで、全体に対する割合(相対頻度)がわかります。(このような操作を、データの正規化といいます)
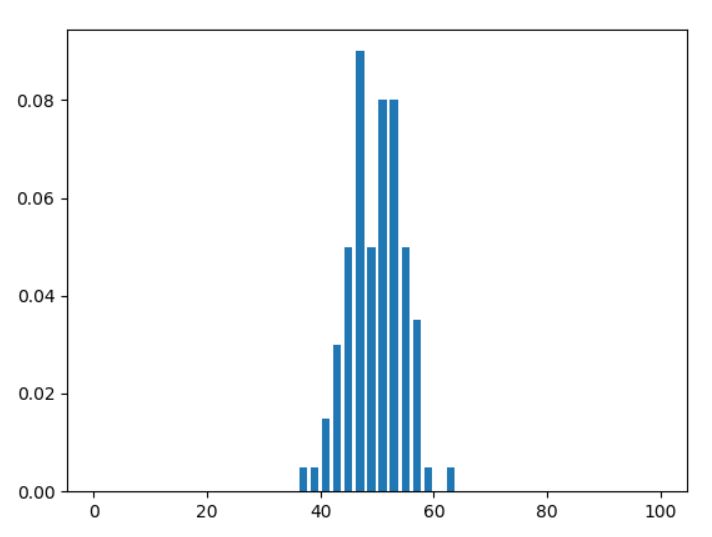
約1割で起こっている結果が100回中50回前後に集中し、100回中40回表のような結果は1%くらいしかない。
こういう割合を、何と言うでしょうか。試行回数を増やしていったときに、相対頻度が近づいていく値ーー長期的な相対頻度、全体に対するある結果の起こりやすさーーそれを確率(probability)というわけです。起こりうる結果を、事象(event)というわけです。
起こっていることが珍しいことなのか、ありふれたものなのか。平均して頻度はどのくらいなのか、試行ごとに結果はどのくらいばらつくのか。こうした疑問は、確率(の分布)さえわかれば解消できます。
しかし、それは簡単なことではありません。コイン投げなどの場合は、確率が理論的に求められます。つまり、特定の事象が起こる場合の数/可能なすべての場合の数、です。しかし、例えばある町に住む人々の身長について、それがどのような確率で決まるかはわかりません。どんな確率を用いれば良いかは、自明ではないのです(だから統計学が必要になります)。
そこで、分布の出番です。真の確率がわからなくても、データは集められます。データが増えれば、頻度分布を書くことで、どの結果が起こりやすいかがだんだんと見えてくるわけです。
統計的な推論で主なものは、調べたい現象に対して、試行によって得られるデータを参考に、真の分布をよく近似しているであろう適切な分布(確率モデル)を見つけ出す、というものです。良いモデルが見つかれば、予測をすることもできるようになるでしょう。
確率分布
統計学における頻度分布と確率の関係、なんとなくわかっていただけたでしょうか。
今まで話したことは感覚的なもので、これをもう少し数学的に厳密な言葉遣いで考えていきましょう。
多少の測度論、公理的確率論の知識を前提にします。が、わからなくてもだいたい読めるかと。
以降の用語の定義はホーエル「入門数理統計学」と熊谷「確率論」を参照しています。測度論、ルベーグ積分の基礎知識は吉田「ルベーグ積分入門」。)
典型的な説明
例えばホーエルの「入門数理統計学」では、確率、確率変数について触れたあとで、特定の確率分布として、二項分布(binomial distributin)や正規分布(normal distribution)が紹介されます(他にも多くの分布が紹介されます)。
\[ \begin{aligned}{{\displaystyle f(x) = {}_n C_x \, p^x (1-p)^{n-x} \quad (x\in \mathbb {N} )}}\end{aligned} \]
\[ \begin{aligned}{{\displaystyle f(x)={\frac {1}{\sqrt {2\pi \sigma^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma^{2}}}\right)\quad (x\in \mathbb {R} )}}\end{aligned} \]
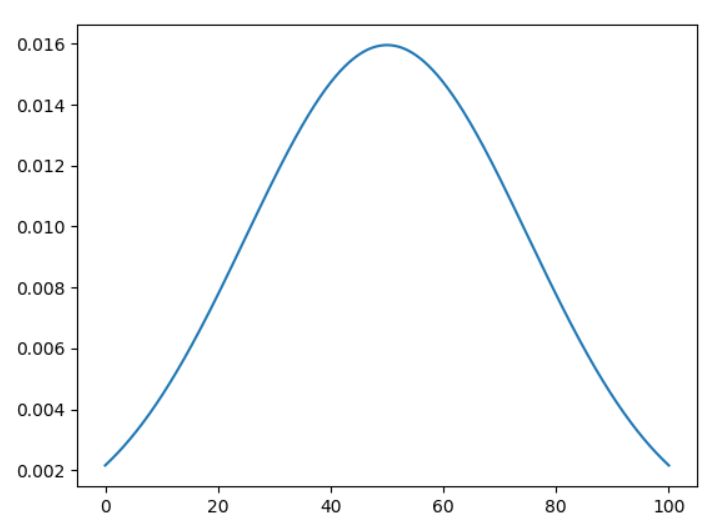
初めて学んだとき、少し混乱しました。正規分布です、と図が出てくる。じゃあ分布って何なのか。\(f\)は分布なのか?それとも確率密度関数なのか? 分布を\(f\)で与えるとしたら、それまでに考えてきた確率や確率変数の議論との関係はどうなっているのか?
順番に用語を整理していきましょう。
確率(測度)、確率変数
集合\(\Omega\)とその上の可算加法族\(\mathcal{F}\)、そこで定義された測度\(P\)の組を、可測空間(measurable space)というのでした。
特に測度が\(P(\Omega)=1\)を満たすとき、それを確率測度(probability measure)、空間を確率空間(probability space)と呼び、集合\(\Omega\)を標本空間(sample space)と呼びます。
高校までに習う確率論と照らし合わせてみましょう。
6面が同様に確からしく出るサイコロにおいて、偶数の目が出る確率は\(3/6 = 1/2\)といったように表されました。
標本空間は、可能な状態すべてを表すものです。6つの出目があるので\(\Omega=\{\omega_1,\dots,\omega_6\}\)としましょう。
加法族は、有限集合の場合は部分集合の全体とすれば良いです\(\mathcal{F}= 2^{\Omega}\)。
調べたい事象とは、標本空間\(\Omega\)の部分集合(可測集合)のこと。偶数の目が出る事象なら、\(B= \{\omega_2,\omega_4,\omega_6\}\)です。
そして確率測度は、\(P(A)= \frac{|A|}{|\Omega|}\)と定義されたものです。ここで、\(|S|\)は集合\(S\)の濃度、有限集合では元の個数。つまり、\(P(B)=1/2\)ですね。
確率変数
もう少し複雑な試行を考えるときには、確率変数(random variable)という概念を使うとわかりやすくなります。
例えばサイコロを2つ振ったときの出目の和が10以上になる事象(\(C\))の確率を考えたいとしましょう。
標本空間としては\(\Omega^2\)を考えることになります。となると、\(C\)がどのような集合なのかを書くのはめんどくさくなってきます。
そこで、確率変数\(X:\Omega ^2 \to \mathbb{R}\)を、標本空間の元に対し出目の和が対応するように定めます。そうすれば、\(P(C)= P(X\geq 10)\)といったように書けるわけです。
一般に、次のような記法を使います。
\[ \begin{aligned}(X=x) := X^{-1}(\{x\}) =\{\omega \in \Omega \mid X(\omega) =x\}\end{aligned} \]
\[ \begin{aligned}(X\in A) := X^{-1}(A) \end{aligned} \]
(こういう書き方、教科書では明示的に書かれていないことが多くて困ります笑)
試行が複雑になるほど、確率空間\(\Omega\)やその部分集合である事象は捉えにくくなってきます。標本空間の言葉を数字に置き換えてくれるのが、確率変数\(X\)の役割です。
一般に\(X:\Omega \to \mathbb{R}\)が確率変数であるとは、(\(\mathscr{F}\)-可測)関数ということだけです。
取りうる値が有限集合もしくは可算集合のときは離散確率変数、そうでないときは連続確率変数と呼ばれます。
(確率的な)事象に応じて値が変わる……それが確率変数、つまり標本空間から実数への関数というわけです。
確率密度関数、確率分布
いよいよ分布の話が整理できます。
確率変数を使えば、(離散の場合)サイコロの出目の和が\(x\)である確率を\(P(X=x)\)と求められます。
ここで変数を\(x\)と見れば、和が\(x\)のときの確率が求められるわけです。つまり、
\[ \begin{aligned}f(x):= P(X=x) \quad x \in \mathbb{N}\end{aligned} \]
とすれば、関数\(f:\mathbb{N}\to \mathbb{R}\)が得られます。この\(f\)を離散確率密度関数(discrete probability density function)と呼びます。
連続密度関数\(X\)については、ピッタリ特定の値を取ることはありえません(測度0)。したがって、密度関数の定義は少し変わります。
\(f(x)\geq 0,\int_\mathbb{R} f(x) dx =1 , \int_a ^b f(x)dx = P(a<X<b)) \)
これを満たす関数\(f:\mathbb{R}\to \mathbb{R}\)を、連続確率密度関数(continuous probability density function)と呼びます。長いので、単に密度関数と呼びましょう。
上で紹介した二項分布や正規分布に関する\(f\)とは、密度関数のことだったのです。文脈によっては、分布=密度関数を意味していますね。
ただ、厳密に言えば、確率分布(probability distribution)という言葉があります。
確率分布とは、\( \left( \mathbb{R},\mathscr{B}(\mathbb{R}) \right)\)上の確率測度\(P\)のことです。(ここで\(\mathscr{B}(\mathbb{R})\)はボレル加法族)。二項分布や正規分布も、確率分布のひとつ。
確率空間\(\Omega\)と確率変数\(X\)があると、確率分布が自然に作れます。つまり、\(P_X (A ):= P(X^{-1}(A))\)と。
\(P_X =P\)と省略して書き、標本空間で考えているのか\(\mathbb{R}\)で考えているのか区別せず、自然に同一視して教科書では書かれていることもあります。
(これは一般に\(X\)の像測度、誘導測度、分布、法則……などと呼びます。)
確率変数があれば確率分布を導けて、さらにそこから密度関数によって考えることができます。
(確率空間がある条件を満たすなら、測度をある可測関数の積分として表せる……これはラドン=ニコディムの定理です。つまり、確率密度関数とは、確率測度\(P_X\)のラドン=ニコディム微分\(f=f_X\)と定義されます)
逆に、密度関数\(f\)を既知として、
\[ \begin{aligned}P(A) = \int _A f(x) dx\end{aligned} \]
と試行の確率(確率測度)を決めてしまうこともできるわけです。\(f\)に対応するような確率空間、確率変数を考えれば良いわけです。
「確率変数\(X\)が確率分布\(\mu\)に従う \(X\sim \mu\)」とは、\(X\)の像測度が確率分布となること\(P_X = \mu\)。
密度関数から確率分布を与えると、確率変数\(X\)が自然と決まります。確率変数に対して定義される期待値\(E[X]\)も、確率密度を使って計算できるわけです。
\[ \begin{aligned} E[X] &:= \int_\Omega X(\omega) P(d\omega) \\ &= \int_ \mathbb{R} x f(x) dx \end{aligned} \]
このように、密度関数\(f\)と(確率分布と呼ばれる)確率測度\(P = P_X\)には、自然な対応関係があります。だから、分布という言葉が\(f\)や\(P\)に対して広い意味で使われるわけです(笑)。
累積分布関数
離散確率変数\(X\)に対し、
\[ \begin{aligned}F(x):= P(X\leq x)\end{aligned} \]
と定められる関数\(F\)は累積分布関数( cumulative distribution function)と呼ばれます。連続確率変数なら、
\[ \begin{aligned}F(x):= \int _{-\infty} ^x f(t)dt \end{aligned} \]
です。\(x\)が増すにつれ単調に値が増えていき、やがて1に近づくものですね。
累積分布関数のことを単に分布関数と言ったりしますが、確率分布や密度関数と混同しないように注意しましょう。
確率の理論的には確率測度\(P\)を分布と見るわけですが、データを測定して得られる度数分布の曲線\(f\):確率密度関数を分布と見ることもあります。\(P,X,f\)の世界をスムーズに行き来して計算できるようになると良いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう
統計学の手法に違いはあっても対立はない 「9つの確率・統計学物語」レビュー
確率論はいかに科学へ応用されたか? 「確率の哲学的試論」を読む