どうも、木村(@kimu3_slime)です。
今回は、勾配降下法をPythonで書き、ガンマ関数の極小値を調べる方法を紹介します。
勾配降下法(やその変化形)は、統計学における最小二乗問題や最尤推定、機械学習に応用されるようです。
勾配降下法はなぜ必要なのか
与えられた関数の最小値を求める問題は、科学全般でよくあります。例えば誤差やエネルギーを最小化したい。
このように、関数の値を最小化、または最大化する問題全般は、最適化問題(optimization problem)と呼ばれます。
この問題については、高校数学でその一部が扱われています。すなわち、微分=0となる極値点を計算して、極値を求める問題です。増減表を書くやつです。
むしろ、微分=0の式で極値点が求められるのに、どうして他の方法(例えば勾配降下法)が必要なのだろうか? と僕は最初に疑問に思いました。
例えば、PythonのモジュールSymPyには、極限計算や微分・積分を、(数値的にでなく)代数的に計算できる関数があります。
これを使えば、センター試験レベルの数学の極値問題は解けます。それこそ、多項式関数の微分はDerivative関数でポンと出て、それをsolve関数で解けば、極値の候補は求まるわけです。
しかし、この方法は比較的シンプルな初等関数のみ可能で、あらゆる関数に通用するわけではありません。
(勾配降下法の説明で、単純な多項式関数の極小値を求めることがありますが、それならば微分を代数計算すればいいのに……と思います)
代数的な微分=0となる値が求められないちょうど良い例が、ガンマ関数(Gamma function)でした。それは次の広義積分によって定義されます。
\[ \begin{aligned}\Gamma (z) = \int _0 ^{\infty} t^{z-1} e^{-t} dt\qquad z \in \mathbb{C}\end{aligned} \]
\(\Gamma(n+1)= n! \quad(n\in \mathbb{N})\)という関係を持つように、階乗関数の一般化となる関数です。
ガンマ関数は複素変数で定義できますが、ここでは正の実数\(x \in (0, \infty)\)について考えましょう。
簡単に計算できる値としては\(\Gamma(1/2)=\sqrt{\pi},\Gamma(1)=\Gamma(2)=1\)があり、\(x\)につき単調増加となっています。\(1,2\)の間のどこかで最小値をとっているような気がしますが、それはどこなのでしょうか?
これをsympyで計算してみようとすると、失敗します。
ガンマ関数の微分をDerivativeで求めると「gamma(x)*polygamma(0, x)」となり、これをsolveしようとすると、
1 2 | NotImplementedError: No algorithms are implemented to solve equation gamma(x) |
つまり、ガンマ関数を含む方程式を解くアルゴリズムが用意されてないと言われています。
これはまさに、微分=0がコンピュータで代数的に計算できない例としてピッタリです。
(ちなみに、ガンマ関数は数学的に微分可能です。しかし、それもまた積分を使って定義される関数で、=0となる点を見つけるのは難しいでしょう。 参考:ガンマ関数とベータ関数 – 清野和彦)
勾配降下法の仕組み、プログラム例
勾配降下法(gradient descent method)の仕組みについて、簡単に紹介しましょう。
そもそも極小点とは、\(\frac{df}{dx}(x) =0\)となる\(x\)のことでした。
勾配法は、どこか適当な点\(x_0\)から出発し、反復計算によって極小点にたどり着く方法です。
その計算は、
\[ \begin{aligned} x_{\mathrm{new}} = x_{\mathrm{old}} – \lambda \frac{df}{dx}( x_{\mathrm{old}})\end{aligned} \]
によって値を更新していくものです。ここで、\(\lambda\)は小さな正数(今回は\(10^{-4}\))で、ステップ幅と呼ばれます。
もし極値にたどり着いていなければ、\(\frac{df}{dx}( x_{\mathrm{old}})\)は正または負となり、これに従い\(x\)が変化してゆきます。つまり、各点の傾き・勾配に応じて、谷底を下っていくように探索していく。これが勾配降下法の名前の由来です。
この更新は、\( |x_{\mathrm{new}} – x_{\mathrm{old}} | < \varepsilon\)となるまで続けます。\(\varepsilon>0\)は小さな数で、今回は\(10^{^-10}\)。
ステップ幅に応じて\(x\)を動かしていく数値計算を行うため、厳密に\(0\)になるまでには時間がかかります。更新による移動幅が\(\varepsilon\)となったところで、勾配0とみなすわけです。
また、微分の計算は今回代数的には難しいので、数値微分、中央差分を用いました。これはテイラー展開から導かれる近似式です。
\[ \begin{aligned}f(x) \approx \frac{f(x+h)-f(x-h)}{2h}\end{aligned} \]
参考:第70回 微分・積分の数学 数値微分 [中編] – gihyo.jp
では、プログラム例と実行結果を紹介しましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | # coding: utf-8 import numpy as np import matplotlib.pylab as plt import scipy.special # 極小値を調べたい関数の定義 def function_1(x): return scipy.special.gamma(x) # 数値微分 def numerical_diff(x): h = 1e-4 return (function_1(x + h) - function_1(x - h)) / (2 * h) # 中心差分 # 勾配降下法 def grad_descent(x0): epsilon = 1e-10 step_size = 1e-4 x_old = x0 # 初期値 # その点での微分係数に応じて、xを動かす x_new = x_old - step_size * numerical_diff(x_old) # 更新の幅がイプシロンより小さくなるまでは繰り返す while abs(x_old - x_new) > epsilon: x_old = x_new x_new = x_old - step_size * numerical_diff(x_old) # print(abs(x_old - x_new)) #動作確認 return x_new # グラフに接線を引く def tangent_line(x): d = numerical_diff(x) print("傾き", d) b = function_1(x) - d * x return lambda t: d * t + b # 勾配法を実行し、極小点、極小値を表示 g = grad_descent(2) print("極小点 {0}, 極小値 {1}".format(g, function_1(g))) # 調べたい関数のグラフ、接線のグラフを表示 x = np.arange(0.2, 4.0, 0.1) y = function_1(x) plt.xlabel("x") plt.ylabel("f(x)") tf = tangent_line(g) y2 = tf(x) plt.plot(x, y) plt.plot(x, y2) plt.ylim(min(x), max(x)) plt.gca().set_aspect("equal") plt.show() |
1 2 | 極小点 1.461633313251917, 極小値 0.8856031944114735 傾き 9.998807337652238e-07 |
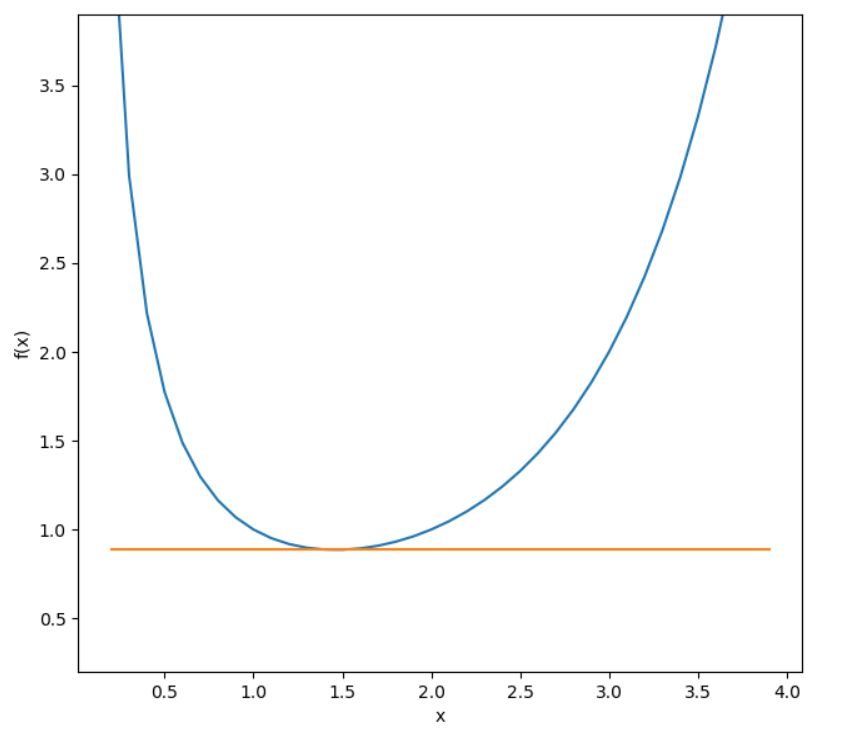
\(x\approx 1.46\)に極小点があることがわかりました! これは手計算で求めるのは大変ではないかと思います。
今回の勾配降下法の出発点は\(2\)となっていますが、別の出発点\(0.5\)から出発しても、求まる極小点は\(1.46163…\)の桁までは一致します。いくつかの初期値を試したほうが、妥当な値と信頼しやすくなるでしょう。
また、今回書いたプログラムはガンマ関数以外の多くの関数(1回微分可能な関数)に適用できます。ただし、極小値にたどり着けるならという限定がつきますが。ぜひ、試してください。
またまた、極大値を求めるときも同様の方法で計算でき、勾配上昇法(gradient ascent method)と呼ばれます。更新する方向を変えれば良いだけ。
\[ \begin{aligned} x_{\mathrm{new}} = x_{\mathrm{old}} + \lambda \frac{df}{dx}( x_{\mathrm{old}})\end{aligned} \]
勾配降下法の問題点と応用
今回は、1変数関数の極値を求めましたが、勾配\(\mathrm{grad } f\)を考えれば多変数でも対応できます。
勾配降下法は、出発した点から各点での勾配に導かれるままに極小点を探します。したがって当然、探したい範囲での大域的な最小値にたどり着けるわけではありません。
例えば、ルジャンドル多項式の極値を調べてみます。scipyでは、n次のルジャンドル多項式は「scipy.special.eval_legendre(n,x)」で計算できます。11次ルジャンドル多項式に対し、初期値0から出発すると、極値にはたどりつきますが、より低い値を取る点もあります。
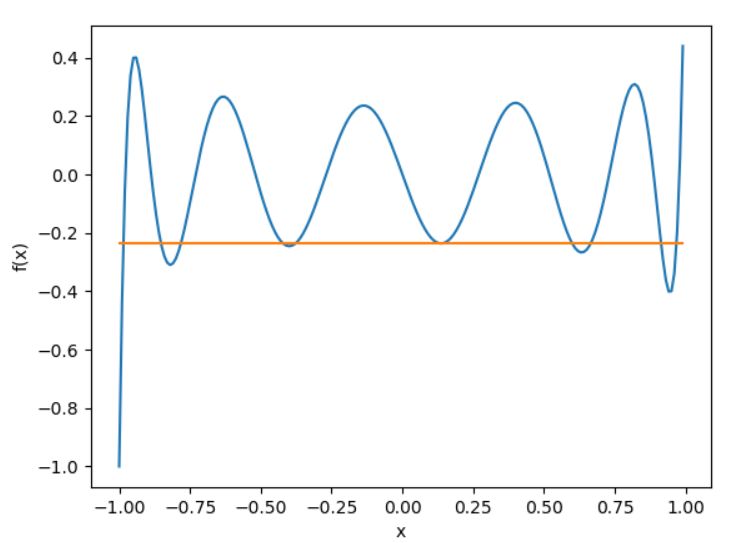
初期値を0.9にしてみると、より低い極値に辿り着けました。グラフのようすが見てわかるレベルなのは大事ですね。(定義域を広くとれば、マイナスの方向はいくらでも小さい値があるわけですが…)

ガンマ関数のように、(大域的に)凸関数については極値にたどり着きやすいですが、凸凹が多かったら、実行がきちんとストップするかどうか、出発点をいくつ試しても最小化点にたどり着けるかわからないでしょう。
最小値を調べたい関数(目的関数)が多くの関数の和で表されるとき、反復計算にランダム性を加えた確率的勾配降下法(stochastic gradient descent, SGD)なるものが知られているようです。
もし何かの問題を「関数を最小化すること」にできたら、そのときは勾配降下法が役立つかもしれない。万能ではありませんが、汎用性のある方法だと思いました。
木村すらいむ(@kimu3_slime)でした。ではでは。
オライリージャパン
売り上げランキング: 62,016
こちらもおすすめ
ネイピア数eをPython(decimal)で100桁計算してみよう
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう