どうも、木村(@kimu3_slime)です。
最近、Pythonによるプログラミングを少しずつ勉強していて、理論的な数学の世界との違いに驚くことがあります。
今回は、2次方程式をプログラムで数値的に解くときに登場する「誤差」の話をします。
2次方程式をプログラムで解く
2次方程式を解くことは、実数\(a,b,c\)を係数として
\[ \begin{aligned}ax^2+bx+c=0\end{aligned} \]
を満たす\(x\)を求める問題でした。
因数分解を使って導かれる(いわゆる)「解の公式」で、その解は簡単に計算できます。
\[ \begin{aligned}x=\frac{-b\pm D}{2a},\quad D= \sqrt{b^2 -4ac}\end{aligned} \]
これを解くプログラムは、そのまま書けば次のようになります。
1 2 3 4 5 | def quad(a,b,c): D=(b**2 - 4*a*c)**(1/2) x_1 = (-b+D)/(2*a) x_2 = (-b-D)/(2*a) print(x_1,x_2) |
いろいろな値について計算すると、概ね妥当な結果が返ってきました。
桁落ち誤差とは?
数値計算に関する情報を調べるうちに、この計算方法では「誤差」が生じるケースがあることを知りました。
例えば、\(a=1,b=1000.001,c=1\)の場合を考えてみます。
\(b=10^3 + 10^{-3}\)と見れば、厳密解が\(x=-0.001,-1000\)であることがわかります。
しかし、さきほどのプログラムで計算させてみると様子が違います。
1 | -0.0009999999999763531 -1000.0 |
厳密解\(x=-0.001\)に非常に近い値ですが、誤差が発生しています。
これは桁落ち誤差(Loss of significance)と呼ばれる現象です。
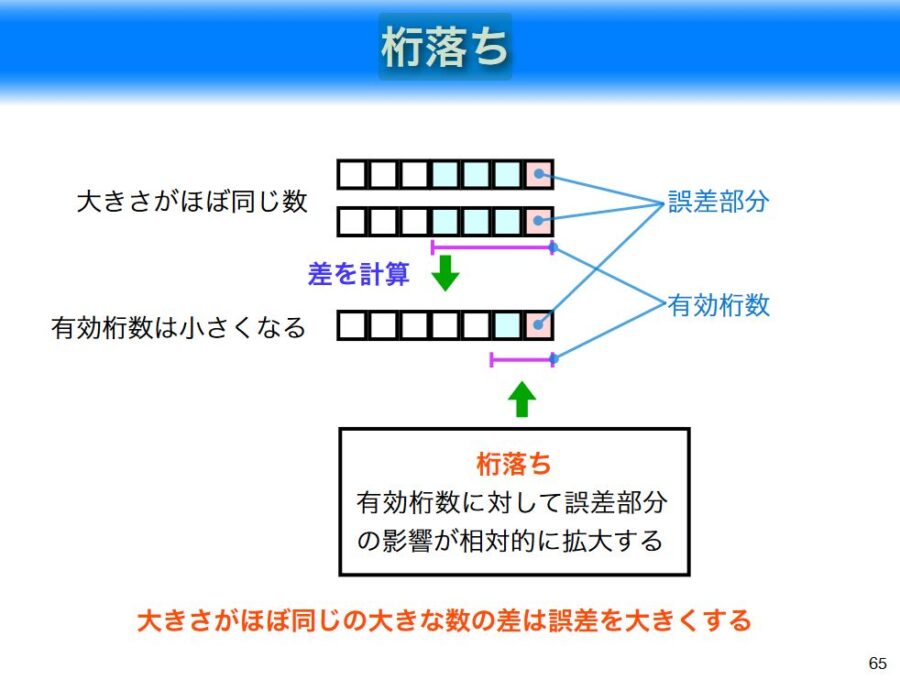
画像引用:Python による科学技術計算の概要 – 神嶌 敏弘
今回の係数では\(b^2\)に対し\(ac\)が小さく、\(D\approx |b|\)となるので、解の計算式において\(-b+D\)が絶対値がほぼ同じ数の加減算になってしまっています。
もともと、コンピュータ(float、浮動小数点数演算)は、無限桁の小数を扱えず、下の位を打ち切って記憶しています。これは丸め誤差(round-off error)と呼ばれるものです。
絶対値がほぼ同じ数の加減算などによって、有効桁数が減り、丸め誤差の影響が相対的に大きくなってしまう……これが桁落ち現象というわけです。
今回のケースでは、桁落ち誤差を回避できます。
問題は分子で行われる計算なので、式変形によってを取り除きましょう。
問題のある方の解\(x_1=(-b+D)/2a\)において、\(-b-D\)をかけて整理します。すると、
\[ \begin{aligned}x_1=\frac{2c}{-b-D}\end{aligned} \]
となります。ちなみに、これは解と係数の関係(Vieta’s formulas)\(x_1 x_2 = c/a\)によって計算するのと同義です。
修正した式によってプログラムを実行すると
1 | -0.001 -1000.0 |
と厳密解と同じ値が得られます。
数値計算には必ず誤差が伴う
プログラミングによる数値計算を勉強しはじめて、桁落ち誤差のことを知ると、「ただ引き算をするだけなのに誤差が生じるのか」と思いました。
シンプルな計算:四則演算1つで誤差が生じてしまっては、より複雑なプログラムになったときに、誤差がどこでどのように起こっているのか見抜くのが大変だろう、と。
そうしてコンピュータの数値計算について調べるうちに、もう少し柔軟な考えをするようになりました。
コンピュータによる計算、というかfloat(浮動小数点数の演算)では、当然誤差が起こるのです。純粋数学的な観点では、誤差が起こる時点で計算は間違いでは……と思ってしまいがちですが、誤差を前提として受け入れるのです。
例えば、\(0.1\)は数学的にはシンプルな数(有理数)です。しかし、コンピュータは2進法にもとづいて数を理解します。2進法では、\(0.1\)は循環小数\(0.00011001100110011…\)となります。
この数を有限桁として保存すれば、当然捨てられる部分があり、近似値となります。floatを使う時点で、丸め誤差は当然入っているのです。
Pythonでは、floatの値を有理数として表現するfloat.as_integer_ratio() メソッドがあります。それによると、
\(0.1 \approx 3602879701896397/36028797018963968\)
とされています。内部的にはかなりの桁の有理数を使って精度の良い近似をしていて、ただし計算結果として普通に表示されてるときはゴタゴタは見せず0.1としている……という工夫が感じられますね。
このような内部事情を知ると、\(0.1 + 0.1+0.1-0.3\)の数値計算が\(0\)にならないことも納得です(\(10^{-17}くらいの数が出てくる\))。10進の世界では当然\(0\)ですが、2進数として計算させていることを考えれば仕方のないことです。
したがって、極めて小さな誤差は、目的に関して問題がなければ無視すれば(roundで桁を丸めれば)良いでしょう。
桁落ちのような誤差が拡大する場合は、式変形などによって回避を試みましょう。純粋な数学と違い、計算結果は計算方法に依存します。誤差の少ないような方法をコンピュータに与えたほうが良いでしょう。floatではなくintで計算できる場面があれば、
有理数を10進数として正確に扱いたい場合はfractions モジュールやdecimal モジュールを用いると良いでしょう。
参考:15. 浮動小数点演算、その問題と制限 – Pythonドキュメント
コンピュータ科学者のWilliam Kahanは、次のような言葉を残したそうです。
計算結果と真の値が有効性を失うほどの不一致を起こすことは極めてまれである。あまりにまれであり、始終そのことを心配する必要はない。ただし、無視できるほどまれでもない。
引用:数値計算と誤差の話~ 浮動小数点演算はどれくらい信用できるか ~渡部 善隆
誤差を恐れては数値計算はできませんが、誤差が入ってきているということは忘れてはいけませんね。
数を代数的に厳密なまま扱える数式処理(計算機代数)や、誤差の程度を評価できる精度保証付き精度計算といったトピックがあり、これらも少しずつ勉強していけたらなと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
オライリージャパン
売り上げランキング: 62,016
こちらもおすすめ
「AならばB」は「Aでない、またはB」を真偽値の計算(プログラミング)で確かめる
論理に関するド・モルガンの法則を真偽値の計算(プログラミング)で確かめる
コンピュータによる計算(アルゴリズム)とは何か、モデル化の方法、その限界は?