どうも、木村(@kimu3_slime)です。
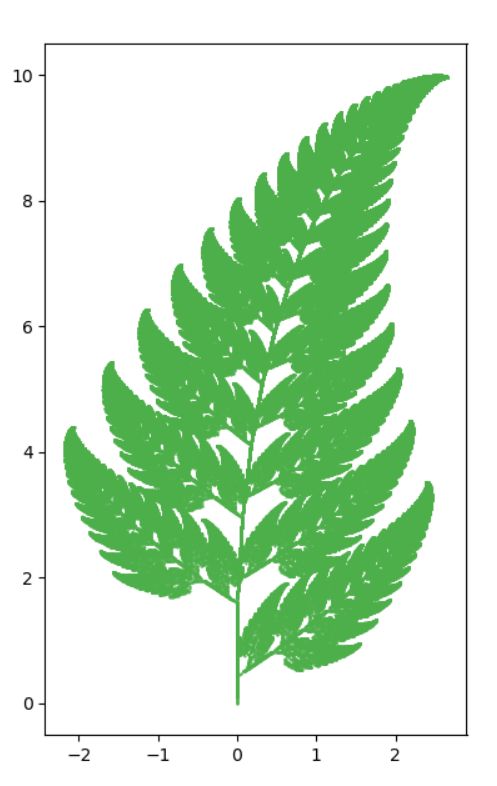
今回は、バーンスレイのシダ(Barnsley fern)と呼ばれるフラクタル図形を、Pythonで描く方法を紹介します。

参考:Real lady ferns. – Sanjay ach
プログラムの紹介
さっそくプログラム例を紹介しましょう(「Pythonからはじめる数学入門」を参考にしています)。
少し長いですが、コメントで説明が書いてあります。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | import random import matplotlib.pyplot as plt def transformation_1(p): # 85%でこれが選ばれる。茎を右上へ伸ばしていく。時計回りに少し回転させ、少し小さくする。大きく上にシフトする。 x = p[0] y = p[1] x_1 = 0.85*x + 0.04*y y_1 = -0.04*x + 0.85*y + 1.6 return x_1,y_1 def transformation_2(p): #茎に対して左側の葉っぱを作るように左大回転、かなり小さくする。大きく上にシフトする。 x = p[0] y = p[1] x_1 = 0.20*x - 0.26*y y_1 = 0.23*x + 0.22*y + 1.6 return x_1,y_1 def transformation_3(p): #茎に対して右側の葉っぱを作るように右大回転、かなり小さくする。少し上にシフトする。 x = p[0] y = p[1] x_1 = -0.15*x + 0.28*y y_1 = 0.26*x + 0.24*y + 0.44 return x_1,y_1 def transformation_4(p): # 中央下部の茎を作る。今までの横推移(x)を中央(0)に戻し、下部の茎まで戻す。いわばリセット。 x = p[0] y = p[1] x_1 = 0 y_1 = 0.16*y return x_1,y_1 def get_index(probability): #乱数に応じて、変換を割り当てる指数を決める r = random.random() # 乱数 0<=r<=1 を生成する c_probability = 0 sum_probability = [] for p in probability: c_probability += p # 確率リストの値をc_probabilityに加えていく sum_probability.append(c_probability) # c_probabilityをリストに追加する for item, sp in enumerate(sum_probability): # itemをインデックス、spをそのインデックスでのリストの値とする if r <= sp: return item # 乱数<=リスト(sum_probability)の値になったとき、そのインデックス(0,1,2)を返す。 return len(probability)-1 # sum_probabilityの値がすべてrより小さいなら、インデックスは3とする def transform(p): # 点pを確率的に変換して返す transformations = [transformation_1, transformation_2, transformation_3, transformation_4] probability = [0.85,0.07,0.07,0.001] # それぞれの変換が選ばれる確率を指定 tindex = get_index(probability) # 確率に応じて1~4のインデックスを決める x,y = transformations[tindex](p) # 決まったインデックスの変換を施す return x,y def draw_fern(n): #全体を描写する x=[0] y=[0] x_1,y_1 = 0,0 #初期値は(0,0) for i in range(n): x_1,y_1 = transform((x_1,y_1)) # 確率的に点を変換する x.append(x_1) y.append(y_1) # 変換した点をリストに保存し、その点を再び変換していく return x,y x,y = draw_fern(500000) # プロット数。多いと時間がかかるので各自調整。 plt.plot(x,y,'.',markersize=1,color='#4daf4a') plt.show() |
内容を簡単に紹介しましょう。
まず、\((0,0)\)に点が打たれます。その点を変換(transformation)で繰り返して移していき、できあがるのがシダの図形です。
変換は4種あり、点を打つ度に1つがランダムに選ばれます。1つは茎・葉を伸ばす。2つは、茎に対して左もしくは右の葉を作る。最後は、最初の茎に戻ってリセットする。4つの変換の繰り返しなので、そう難しくはありませんが、できあがる図形はそれらしいものですね。
今回の変換は、\(A\)を\(2\times 2\)の行列として、\(f(x)= Ax +b\)と表されます。線形変換\(Ax\)に平行移動\(b\)を加えた変換は、一般にアフィン変換(Affine transformation)と呼ばれます。
特に、最もよく選ばれる1番目の変換の線形変換の部分に注目してみましょう。
\[ \begin{aligned}\begin{pmatrix} 0.85 & 0.05 \\ -0.05 & 0.85 \end{pmatrix}= c\begin{pmatrix} \cos \theta & \sin \theta \\- \sin \theta & \cos \theta \end{pmatrix}\end{aligned} \]
これは回転行列と呼ばれるもので、(\(\sin\)の符号に注意して)時計回りに\(\theta\)だけ回転させる変換を表しています。(\(c\approx 0.851\)は倍率を定める適当な定数)
数値的に計算してみると、約\(3.37^{\circ}\)の回転です。この角度で曲がりながら、\(y\)軸のシフト\(1.6\)によって斜め右上に進んでいくように見えるわけです。
今回紹介した図形は、イギリスの数学者バーンスレイが著書「Fractals Everywhere」で提案したものです。
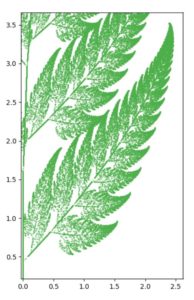
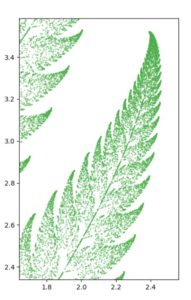
この図形は、拡大しても拡大しても、同じような図形が登場します。このように、部分と全体が自己相似になっている図形は、一般にフラクタル(Fractals)と呼ばれています。
フラクタルは、湾岸地域の地形(リアス式海岸)や、ブロッコリーの仲間であるロマネスコなど、自然によって作られる形を近似しているように見えます。(フラクタル生成と同様の仕組みが働いているかどうかはわかりませんが)

画像引用:A Broccoli variety Romanesco, grown in the field –
また、今回紹介したシダ以外にも、シェルピンスキーのギャスケット、雪印曲線(コッホ曲線)、メンガーのスポンジ、マンデルブロ集合など、よくわからなくても見ていて楽しいフラクタルは多くあります。
ぜひ、フラクタルについて調べて、今回のシダのプログラムに触れてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
オライリージャパン
売り上げランキング: 62,016
筑摩書房
売り上げランキング: 315,630
こちらもおすすめ
ネイピア数eをPython(decimal)で100桁計算してみよう