どうも、木村(@kimu3_slime)です。
今回は、スカラー場、ベクトル場の線積分とは何か、簡単な例、求め方を紹介します。
スカラー場の線積分とは
スカラー場とは、多変数の実数値関数\(f:\mathbb{R}^N \to \mathbb{R}\)のことです。
例えば、\(N=2\)のとき、\(f_1(x,y)=2x-3y\)や\(f_2(x,y):=x^2+y^2\)はスカラー場です。定義域は平面\(\mathbb{R}^2\)であり、そのグラフは空間における平面や曲面を表します。
スカラー場の値は実数値であり、各点における高さや温度を表すものとしてイメージすると良いでしょう。
さて、スカラー場の変化量の和、積分を考えたいとしましょう。
高校までの積分では、実数値関数\(f(x)\)を実数直線\(\mathbb{R}\)上で積分することを考えました。積分の範囲は、\(a<x<b\)といった線分です。
多変数の関数\(f(x,y)\)となれば、足し合わせる経路としてさまざまなものが考えられます。その経路は、一般に曲線(curve)で、曲線に沿った積分を考えるから線積分(curve integral)と呼ばれます。
平面や空間における曲線は、数学的には、1変数のベクトル値関数\(c:[a,b]\to \mathbb{R}^N\)として捉えられます。パラメータ付けられた曲線であり、時間\(t\)とともに、点\(c(t)\)が動くイメージ。今回は、次の図のような曲線を考えましょう。
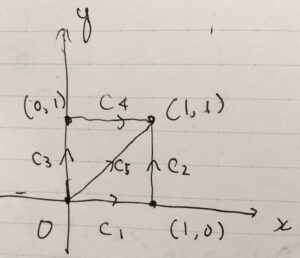
\(c_1(t)=(t,0)\)、\(c_2(t)=(1,t)\)、\(c_3(t)=(0,t)\)、\(c_4(t)=(t,1)\)、\(c_5(t)=(t,t)\)です。どれも定義域は\([0,1]\)です。今回は直線ばかりですが、曲がった経路を考えることはいくらでもできます(\(c\)は適度になめらかなら何でも良い)。
スカラー場\(f\)の経路\(c\)上の線積分は、
\[ \begin{aligned}\int _c f :=\int_a ^b f(c(t)) \| c^{\prime }(t)\| dt\end{aligned} \]
と定義されます。ここで\(\|c^{\prime }(t)\|\)はノルム(大きさ)で、\(c(t)=(c_x(t),c_y(t))\)のとき、\(\|c^{\prime }(t)\|=\sqrt{(c^{\prime}_x (t))^2+(c^{\prime}_y (t))^2}\)です。
これは1変数実数値関数の積分の一般化となっています。\(f_3(x,y)=g(x)\)と実質的に1変数のスカラー場を考えて、経路\(c_1\)での線積分を計算してみましょう。
\[ \begin{aligned}\int_{c_1} f_3 = \int _0 ^1 f_3(c_1 (t)) \|c_1^{\prime}(t)\| dt=\int _0^1 g(t) dt \end{aligned} \]
これは高校までで考えた積分と全く同じです。また、\(f_4(x,y)=1\)というスカラー場を考えて、一般の曲線\(c\)における積分を考えれば、
\[ \begin{aligned}\int_ c f_4 =\int _a ^b \|c^{\prime}(t)\| dt\end{aligned} \]
これは曲線\(c\)の長さにほかなりません。1変数関数の積分では、\(\int_b ^a 1 dx =b-a\)と区間の長さが出てきましたが、線積分は同様の性質を保っています。(そうなるような和を考えたのです)
\(f_1(x,y)=2x-3y\)について、いくつかの経路\(c_1(t)=(t,0)\)、\(c_2(t)=(1,t)\)、\(c_5(t)=(t,t)\)で線積分を計算してみましょう。速度\(\| c^{\prime }(t)\|\)をかけるのを忘れないように。
\[ \begin{aligned}\int_{c_1} f_1 =\int_0 ^1 2t \cdot 1 dt=1\end{aligned} \]
\[ \begin{aligned}\int_{c_2} f_1 =\int_0 ^1 (2-3t)\cdot 1 dt=\frac{1}{2}\end{aligned} \]
\[ \begin{aligned}\int_{c_5} f_1 =\int_0 ^1 (2t-3t) \sqrt{2} dt=-\frac{\sqrt{2}}{2}\end{aligned} \]
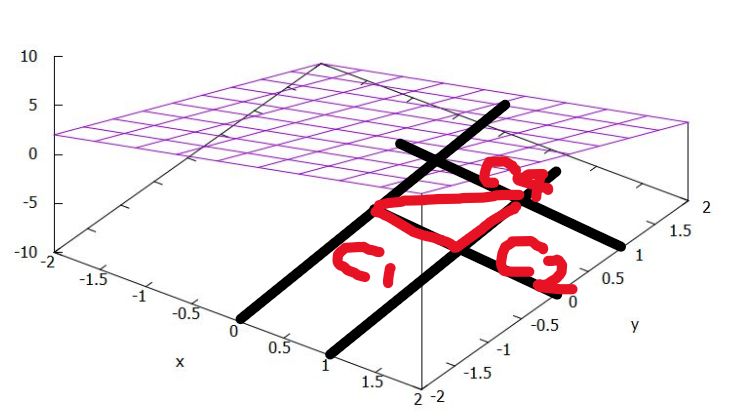
その線積分の値は、経路にそった\(f_1\)の変化を足し合わせたもの、\(z=0\)と\(f_1\)がなすグラフの(符号付き)面積と言えます。\(c_1\)では\(x\)軸方向に、\(c_2\)では\(y\)軸方向に、\(c_4\)では斜めに\(x=y\)グラフを切って、面積を求めたわけです。
ベクトル場の線積分とは
続いて、より一般的なケース、ベクトル場の線積分について考えます。
ベクトル場とは、多変数のベクトル値関数\(f:\mathbb{R}^N \to \mathbb{R}^N\)のことです。\(N=2\)のとき、\(F_1(x,y)=(y,x)\)や\(F_2(x,y)=(y, -x)\)はベクトル場です。
ベクトル場は、自分が平面上の点\((x,y)\)に立っていたとして、そこで向きを持った力\(F(x,y)\)を受けると考えると良いでしょう。風や水によって流されるイメージです。物理では力場、電磁場、流れ場など、さまざまなベクトル場を考えます。
ベクトル場\(f\)の経路\(c\)上の線積分は、
\[ \begin{aligned}\int _c f :=\int_a ^b \langle F(c(t)) ,c^{\prime }(t) \rangle dt\end{aligned} \]
と定義されます。ここで\(\langle F(c(t)) ,c^{\prime }(t) \rangle\)は各成分の積を足し合わせたもの、ユークリッド内積です。
簡単な例で計算してみて、そのイメージを掴みましょう。
\(F_1(x,y)=(y,x)\)を経路\(c_1(t)=(t,0)\)、\(c_2(t)=(1,t)\)、\(c_3(t)=(0,t)\)、\(c_4(t)=(t,1)\)、\(c_5(t)=(t,t)\)上で線積分します。
\[ \begin{aligned}\int_{c_1} f_1 =\int_0 ^1 \langle (0,t) ,(1,0) \rangle dt=0\end{aligned} \]
\[ \begin{aligned}\int_{c_2} f_1 =\int_0 ^1\langle (t,1) ,(0,1) \rangle dt=1\end{aligned} \]
\[ \begin{aligned}\int_{c_3} f_1 =\int_0 ^1\langle (t,0) ,(0,1) \rangle dt=0\end{aligned} \]
\[ \begin{aligned}\int_{c_4} f_1 =\int_0 ^1\langle (1,t) ,(1,0) \rangle dt=1\end{aligned} \]
\[ \begin{aligned}\int_{c_5} f_1 =\int_0 ^1\langle (t,t) ,(1,1) \rangle dt=1\end{aligned} \]
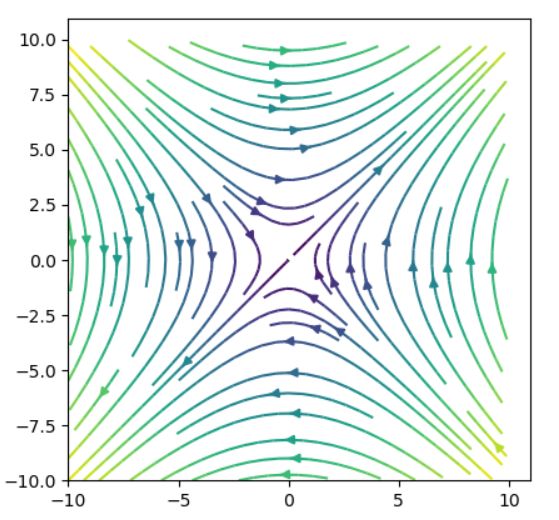
ベクトル場の線積分は、その経路に沿ってどれだけベクトル場から力を受けたかの合計です(物理では、それを仕事という)。経路\(c_1,c_3\)では進む方向とベクトル場が直交しており、何ら力を受け取っていないので、線積分の値が0となっています。
また、\(\int_{ c_1} f+\int _{c_2} f= \int _{c_3} f+\int_{c_4} f =\int_{c_5} f\)であり、\((0,0)\)から\(1,1\)へ向かう線積分の値は、経路によらず一定となっています。このような場は、保存場、ポテンシャル関数を持つ場と呼ばれるものです。保存力を持つ場では、力学的エネルギー保存の法則が成り立ちます。
別の例として、\(F_2(x,y)=(y,-x)\)を経路\(c_1(t)=(t,0)\)、\(c_2(t)=(1,t)\)、\(c_5(t)=(t,t)\)上で線積分します。
\[ \begin{aligned}\int_{c_1} f_1 =\int_0 ^1 \langle (0,-t) ,(1,0) \rangle dt=0\end{aligned} \]
\[ \begin{aligned}\int_{c_2} f_1 =\int_0 ^1\langle (t,-1) ,(0,1) \rangle dt=-1\end{aligned} \]
\[ \begin{aligned}\int_{c_5} f_1 =\int_0 ^1\langle (t,-t) ,(1,1) \rangle dt=0\end{aligned} \]
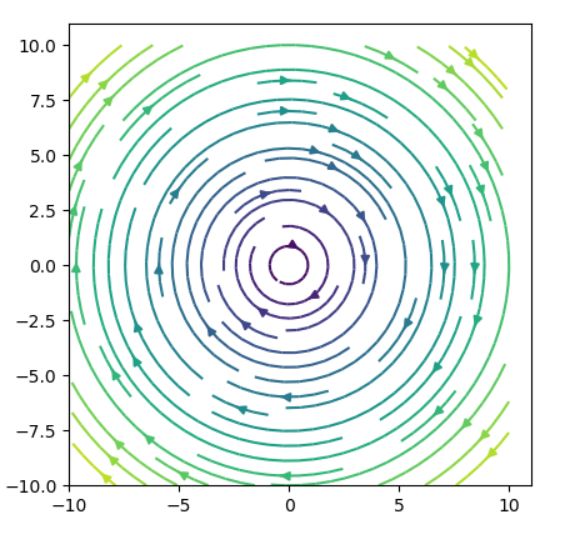
今回は、\(\int_{ c_1} f+\int _{c_2} f \neq \int_{c_5} f\)であり、同じ端点を持つ線積分であっても値が変わっています。このようなベクトル場は、ポテンシャル関数を持たないのです。
以上、スカラー場・ベクトル場の線積分を紹介してきました。それは経路(曲線)に沿って関数を足し合わせたものです。
線積分は、物理に応用される一方で、複素積分の理論においても基本的な存在です。また、平面におけるベクトル場の線積分は、重積分と関係を持っているというグリーンの定理が知られています。
ベクトル場の微積分の理論はベクトル解析と呼ばれますが、ベクトル解析の入門として、線積分の計算と考え方にぜひ馴染んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似