どうも、木村(@kimu3_slime)です。
今回は、球、曲面の接平面の求め方を紹介します。
球の接平面の求め方
2変数関数\(f(x,y)\)のグラフ\(z=f(x,y)\)の\((a,b)\)における接平面は、
\[ \begin{aligned}g(x,y)=f_x(a,b)(x-a)+f_y(a,b)(y-b)+f(a,b)\end{aligned} \]
3次元空間の曲面は、\(z=f(x,y)\)と陽に表されているとは限りません。例えば、球の方程式がそうです。
\[ \begin{aligned}x^2+y^2+z^2 = 1\end{aligned} \]
これを満たす\(z\)を、\(z=f(x,y)\)とただひとつの関数で表すことはできません(円周と同様に)。陰関数表示して接平面を求めることもできますが、今回は別の方法を取りましょう。
\(F(x,y,z)= x^2+y^2+z^2\)と3変数関数\(F:\mathbb{R}^3 \to \mathbb{R}\)を定めます。
実数\(k\)に対して、\(F(x,y,z)=k\)を満たす\((x,y,z)\)は、ひとつの曲面を定めます。例えば\(k=1\)ならば半径が1の球、\(k=3\)ならば半径3の球です。(こうした曲面を、等高面と言います)
\(F\)の勾配ベクトルを
\[ \begin{aligned}\nabla f=(\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z})\end{aligned} \]
と定めれば、\(\nabla f\)は\(F\)が増加する方向を向いています。つまり、曲面に対して(局所的に)直交するベクトル、法線ベクトルとなっています。
そこで\(\nabla f\)を法線ベクトルとして、それと直交する平面を、接平面と呼ぶわけです(定義)。
接平面を具体的に求めてみましょう。
\(F(x,y,z)= x^2+y^2+z^2\)のとき、勾配ベクトルは\(\nabla F(x,y,z)=(2x,2y,2z)\)です。
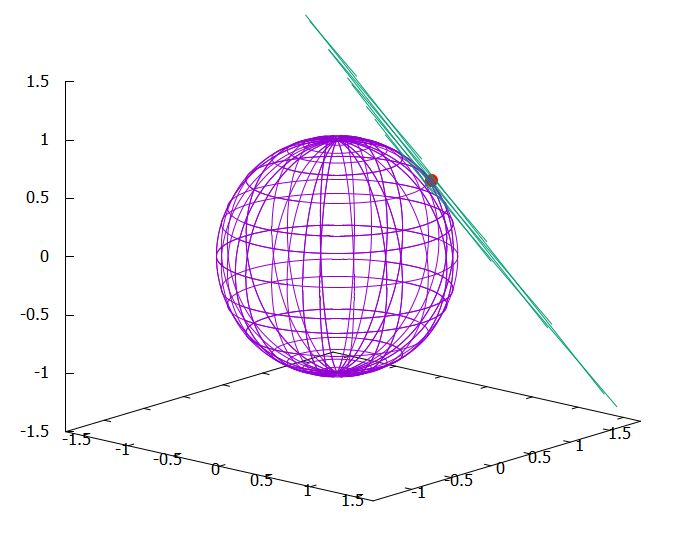
半径1の球上の点\(p_0=(\frac{1}{2},\frac{\sqrt{3}}{2\sqrt{2}},\frac{\sqrt{3}}{2\sqrt{2}})\)における勾配ベクトルは、\(\nabla F(p_0)=(1,\frac{\sqrt{3}}{\sqrt{2}},\frac{\sqrt{3}}{\sqrt{2}})\)。
よって、接平面上の点を\(p=(x,y,z)\)とすると、\(p_0\)から\(p\)へ向かう位置ベクトル\(p-p_0\)と勾配ベクトル\(\nabla F(p_0)\)は直交します。すなわち、内積が0となります。
\[ \begin{aligned}\langle p-p_0,\nabla F(p_0) \rangle=0\end{aligned} \]
\[ \begin{aligned}(x-\frac{1}{2})+\frac{\sqrt{3}}{\sqrt{2}}(y-\frac{\sqrt{3}}{2\sqrt{2}})+\frac{\sqrt{3}}{\sqrt{2}}(z-\frac{\sqrt{3}}{2\sqrt{2}})=0\end{aligned} \]
と接平面の方程式が求められました。
曲面の接平面の求め方
今までの議論は、そのまま一般の曲面に適用できます。
3変数関数\(F:\mathbb{R}^3 \to \mathbb{R}\)によって、\(F(x,y,z)=k\)と表される曲面を考えましょう。点\(p_0\)における接線の方程式は、勾配ベクトルと直交するので
\[ \begin{aligned}\langle p-p_0,\nabla F(p_0) \rangle=0\end{aligned} \]
で与えられます。
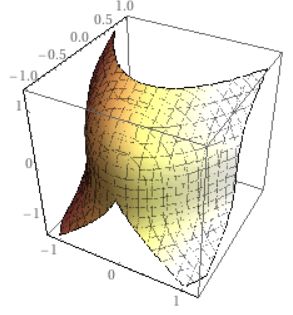
試しに、\(F(x,y,z)=2x^2-3y+z^2\)と\(F=3\)により定まる曲面の、点\(p_0 =(1,1,2)\)における接平面を求めてみましょう。
勾配ベクトルは\(\nabla F(x,y,z)= (4x,-3,2z)\)で、点\(p_0\)においては\(\nabla F(x,y,z)= (4,-3,4)\)です。よって、\(p=(x,y,z)\)とした接平面の方程式は
\[ \begin{aligned}\langle p-p_0,\nabla F(p_0) \rangle=0\end{aligned} \]
\[ \begin{aligned}4(x-1)-3(y-1)+4(z-2)=0\end{aligned} \]
と求められました。

以上、球や曲面の接平面の求め方を紹介してきました。
曲面をある関数の等高面と捉え、その勾配ベクトルと直交する平面として接平面が求められます。
\(z=f(x,y)\)と陽に与えられた曲面はともかく、\(F(x,y,z)=k\)と陰に与えられた曲面がどのような形をしているのかは、一般には非常に捉えづらいです。
しかし、それがある点のまわりで局所的にどんな形をしているか、接平面がどんなものか知ることは、偏微分の計算がわかればできます。曲面を近似する接平面の考え方に、ぜひ馴染んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080