どうも、木村(@kimu3_slime)です。
今回は、陰関数とは何か、2次元における具体例、その微分の求め方を紹介します。
円の方程式と陰関数
平面における半径1で中心が原点が\((0,0)\)の円の方程式は、
\[ \begin{aligned}x^2 +y^2 =1\end{aligned} \]
と表されます。この方程式から、\(x,y\)の対応関係(関数)を取り出すことはできないでしょうか。
\(y\)について整理すれば、\(y ^2 = 1-x^2\)なので、\(0\leq x \leq 1\)において\(y= \pm \sqrt {1-x^2}\)が得られます。円の上側と下側が分かれています。
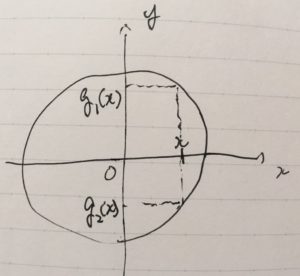
関数とは、与えられた\(x\)に対してただ一つの値を対応させる規則のことでした。なので、\(g(x)=y= \pm \sqrt {1-x^2}\)は関数ではありません(2つの値を持っている)。ただし、\(g_1 (x)=\sqrt {1-x^2} \),\(g_2 (x)=-\sqrt {1-x^2}\)と定めれば、これらは関数となります。
このことを、方程式\(x^2 +y^2 =1\)は関数\(g_1,g_2\)を暗黙のうちに定めていると捉え、\(g_1,g_2\)を陰関数と言います。
少し一般的に定義してみましょう。
\(y= x^2\)など、\(y=f(x)\)の形で定義された関数を陽関数(explicit function)と言います。陰関数と対比させるための言い方で、いわゆる普通の関数のことです。
\(F(x,y):\mathbb{R}^2 \to \mathbb {R}\)を、(適度に微分可能な)2変数関数とします。方程式\(F(x,y)=0\)を満たす点\((x,y)\)は、平面上の何らかの曲線です。この方程式を満たすような関数\(g(x)\)(\(F(x,g(x) )=0\))が存在するとき、\(g\)を陰関数(implicit function)と呼びます。ここで、\(F(x,y)=0\)は陰方程式(implicit equation)とも。
(\(F\)が2変数の多項式関数のとき、\(F=0\)が定める図形は代数曲線と呼ばれます。円や二次曲線は代数曲線の一種です。)
2変数関数について:2変数関数と偏微分:グラフ、接平面を描いてみよう
円の方程式\(F(x,y)=x^2+y^2-1=0\)は、ひとつの陽関数では表せませんが、2つの陰関数で表すことができました。
陰関数の微分の求め方
円や二次曲線など、代数曲線の形を調べるために、各点における陰関数の微分(接線)を計算したくなります。
陰関数が存在するときは、その微分を(比較的)簡単に計算することができます。
まずは少し手間のかかる方法を、あえてやってみましょう。
円の方程式\(F(x,y)=x^2+y^2-1=0\)の例で、\(y>0\)のケース、陰関数\(g_1 (x)=\sqrt {1-x^2} \)を直接微分します。合成関数の微分法より、
\(g_1 ^{\prime} (x) = \frac{1}{2}\frac{1}{\sqrt{1-x^2}} (1-x^2)^{\prime} \\=- \frac{x}{\sqrt{1-x^2}} \)
です。
一方で、\(F(x,y)=x^2+y^2-1=0\)から、そのまま陰関数の微分を計算できます。
\(y>0\)において陰関数が存在するので、\(y\)を\(x\)の関数と考えましょう\(y=g_1(x)\)。そして両辺を\(x\)について微分すれば、\(2x +2y y^{\prime}=0\)です。すなわち、\(y’ = -\frac{x}{y}= -\frac{x}{\sqrt{1-x^2}}\)が得られました。
ここから、(\(y>0\)のときの)円の接線の方程式が求められます。点\((x_0,y_0)\)を通る接線は、\(y-y_0 =-\frac{x_0}{\sqrt{1-x_0^2}} (x-x_0)\)です。\(x_0^2 +y_0^2 =1\)から整理すれば、\(y =-\frac{x_0}{y_0} (x-x_0)+y_0\)となります。
楕円や双曲線などの二次曲線でも、同様の計算ができます。(ただし、パラメーター表示:媒介変数表示できるので、そちらで調べる方が簡単かもしれません。しかし一般の\(F(x,y)\)は簡単なパラメーター表示を持つとは限りません。以降で紹介する例など。)
陰関数が存在するから、\(y\)を\(x\)に関する関数と考えられて、方程式を\(x\)で微分できるようになったことに注意しましょう。陰関数には、通常、限られた定義域があります(局所的に定義されると言う)。「\(F(x,y)=0\)をいきなり\(x\)について微分して~」と議論するのはやや乱暴です(両辺の形式的な微分は、\(y= g(x)\)が存在したと仮定して議論を進めているのと同じ)。
もうひとつ例を考えてみましょう。\(F(x,y)=x^3 -x-y^2 +1\)とします。グラフはどんな形でしょうか。
仮に陰関数\(y=g(x)\)が存在するならば、その微分を計算することができます。
\(F(x,g(x))=0\)の両辺を\(x\)で微分すれば、\(3x^2 -1 -2g(x) g'(x)=0\)です。よって、\(g'(x)= \frac{3x^2 -1}{2y}\)です。例えば、\(y>0\)のとき、\(x<-\sqrt {\frac{1}{3}}\)ならば\(g\)は増加、\(-\sqrt {\frac{1}{3}}<x<\sqrt {\frac{1}{3}}\)ならば\(g\)は減少、\(\sqrt {\frac{1}{3}}<x\)のとき\(g\)は増加します。
また、\(F(x,y)=F(x,-y)\)なのでグラフは\(x\)軸について対称です。そして\(y=0\)となる点は\(x<0\)にしかありません。これらを考慮すれば、次のようなグラフが描けますね。
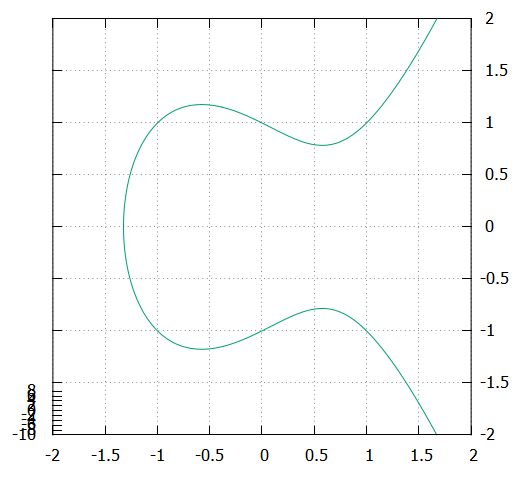
今回は、陰関数とは何か、2次元における具体例、その微分の求め方を紹介しました。\(F\)が3変数以上になっても、陰関数の話はできます。
「もし陰関数が存在すれば」という議論を行いましたが、一般的な条件のもとで陰関数が存在することは、陰関数定理として知られています。それは最適化問題(極値問題、ラグランジュの未定乗数法)や、曲線や曲面を一般化した多様体の構成に応用されます。これらについては別記事で。
\(F(x,y)=0\)で表される図形を調べるときに、陰関数の考え方が役立つことを感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥3,300
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似