どうも、木村(@kimu3_slime)です。
今回は、ゼノンのパラドックス(アキレスと亀)を、高校数学、数列と極限の考え方によって解説していきます。
ゼノンのパラドックス(アキレスと亀)とは
ゼノンのパラドックスとは、古代ギリシャの哲学者ゼノンによって提唱された、矛盾しているように見える奇妙こと=パラドックスです。
いくつかのパラドックスが提唱されていますが、特に有名なのが、アキレスと亀の話。アキレスは、足の部位名:アキレス腱の由来ともなった、足の早い人間の名前です。
走ることの最も遅いものですら最も速いものによって決して追い着かれないであろう。なぜなら、追うものは、追い着く以前に、逃げるものが走りはじめた点に着かなければならず、したがって、より遅いものは常にいくらかずつ先んじていなければならないからである、という議論である
引用:アリストテレス『自然学』第6巻第9章
最初に述べられた結論はどうも奇妙です。早いものはどこかの時点で遅いものに追いつくのではないでしょうか。ポイントは、その次から繰り広げられる議論です。
図解しました。最初にアキレスのいる地点を\(A\)、亀のいる位置を\(B\)とします。
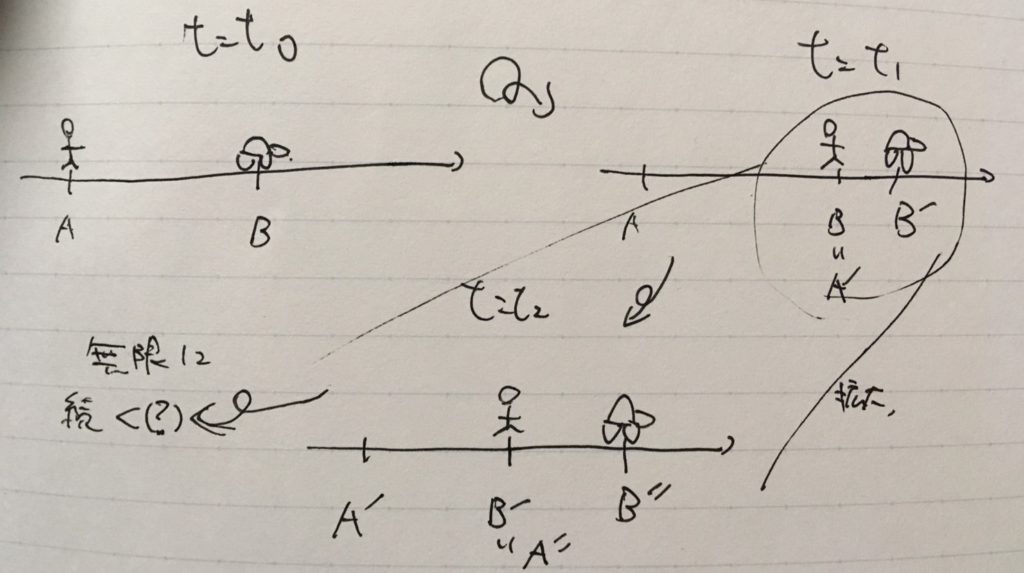
「追うものは、追い着く以前に、逃げるものが走りはじめた点に着かなければなら」ないのは確かです。時刻\(t=t_1\)では、アキレスの位置\(A^{\prime}\)は、亀が元いた位置\(B\)にまで来ています。このとき、亀は\(B\)よりも先の位置\(B^{\prime}\)に移動して追いつかれていません。
ところが、この議論を繰り返すとどうなるでしょうか? さらに先の時刻\(t= t_2\)では、アキレスは亀がいた位置まで来ています\(B^{\prime}= A^{\prime \prime}\)。しかしその間にも亀は進んでいるのですから、\(B^{\prime\prime}\)は\(B^\prime\)より先にあります。これは無限に続くので、一生アキレスは亀に追いつけないのではないか。これがアキレスと亀の話です。
はじめに見たように、結論は間違っています。つまり、論証のどこかにおかしな点があるのです。「これは無限に続くので、一生アキレスは亀に追いつけないのでは」が特に怪しい。
高校数学:数列の極限を使って解釈する
高校数学、数列や極限の考え方を使えば、アキレスと亀の議論を矛盾なく理解することができます。
アキレスと亀は\(x =100\)m離れていて、アキレスは\(v_A =10\)m/s、亀は\(v_B = 1\)m/sと一定の速度移動しているとしましょう。(わかりやすさのため具体的な数字を設定しましたが、距離\(x\)やアキレスと亀の速度は\(v_A >v_B\)である限り、以降の議論は行なえます。)
最初にアキレスが亀がもといた地点に追いつく時間は、\(t_1 =\frac {x}{v_A} =10\)sです。この間に、亀は\(v_B t_1 = 10\)mだけ移動しています。
さらにアキレスが10mだけ移動するのにかかる時間は、\(t_2 = \frac {v_B t_1 }{v_A} =\frac{x v_B^2 }{v_A ^2}=1\)sです。この間に、亀は\(v_B t_2 = 1\)mだけ移動しています。
この議論を繰り返せば、\(t_3 = \frac {v_B t_2 }{v_A} = x \frac{x v_B^3 }{v_A ^3} \)であり、一般の\(n \in \mathbb{N}\)に対しては、\(t_n =x (\frac{v_B}{v_A})^n =100\cdot \frac{1}{10^n}\)です。このようにして定まる数字の列\(t_1,t_2,t_3,\dots\)をまとめたものは、数列\(\{t_n\}_{n \in \mathbb{N}}\)と呼ばれるのでした。
確かにこの議論は、\(n\)を増やしていくことで無限に続けられます。しかしステップが無限にかかることは、かかる時間の合計が無限であることを意味しないのです。
\(k\)回までのステップでかかる時間の合計を、\(S_k\)としましょう。すなわち、
\[ \begin{aligned}S_k = \sum _{n=1} ^k t_n =\sum _{n=1} ^k 100\cdot \frac{1}{10^n} \end{aligned} \]
とします。そして、アキレスが亀においつくまでの時間\(T\)というのは、\(k\)が大きくなっていくときに\(S_k\)が限りなく近づいていく値、すなわち極限値のことです。
\[ \begin{aligned}T =\lim _{k\to \infty} S_k = \lim _{k\to \infty}\sum _{n=1} ^k t_n \end{aligned} \]
\(t_n\)を足し合わせていく行為は、ゼノンの言うように無限に行えます。しかし、アキレスが亀のもといた地点まで移動するのにかかる時間\(t_n=100\cdot \frac{1}{10^n}\)は、\(n\)が大きくなるにつれ小さくなり、ほんの一瞬の時間しかありません。そのため、かかる時間の合計(が近づいていく値)は有限となるのです。
確かめてみましょう。等比数列の和の公式より、\[ \begin{aligned}S_k = 10 \cdot \frac{1-\frac{1}{10^k}}{1-\frac{1}{10}}=\frac{100}{9}(1-\frac{1}{10^k})\end{aligned} \]となります。ここで、\(k\)が大きくなるとき、\(\frac{1}{10^k}\)は限りなく0に近づきます。よって、\[ \begin{aligned}T =\lim _{k\to \infty} S_k = \frac{100}{9}\end{aligned} \]
となります。およそ11秒でアキレスは亀に追いつくことがわかりました。
そもそも、「アキレスの移動距離+最初のアキレス-亀間の距離が、亀の移動距離に等しい」 \(v_A t +x=v_B t \) という関係式を作り、これを満たす\(t\)を見つける問題とも言えます。すると、\(10t+100= t\)、すなわち\(t=\frac{100}{9}\)が得られます。この2つの結果に矛盾はなかったのです。
「無限に足し合わせる操作」は限りなく続きますが、有限和が近づいていく値(極限)は一定なのです。小さい量を無限に足し合わせていく時、それはもちろん無限大に増えていくこともありますが(例:調和級数)、今回のように有限の値に収束することもあります。ゼノンのパラドックス(アキレスと亀)は、極限という考え方が整理されていなかったがゆえに生まれたと言えるでしょう。
このように、高校数学を理解するだけでも、十分に豊かな視点を手に入られます。さらにもし「限りなく近づく値」という極限の定義に曖昧さを感じたら、大学数学の微積分・解析学を学んでみてください。極限の概念は、「無限」というパラドックスを生じそうで取り扱い難いものを、矛盾なく認識する手段を与えてくれています。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
岩波書店 (1968-07T)
¥822 (中古品)