どうも、木村(@kimu3_slime)です。
今回は、「\(0.999\dots =1\)」という式が成り立つのはなぜか、無限小数と数列の極限という高校数学の話を交えて紹介します。
よくある説明
よくある説明は、次のようなものです。
1を3で割って小数で表すと、無限に3が現れるので、\(\frac{1}{3} = 0.333\dots \)が成り立つ。両辺を3倍すれば、\(\frac{1}{3} \times 3 =1 = 0.999 \dots\)が得られた。
もしこれで納得できるならば、この先の文章は読まなくて良いでしょう。
僕の考えでは、これは「\(0.999\dots =1\)」が成り立つ(ような気がする)説明にはなっていても、証明にはなっていません。
- \(0.333\dots, 0.999\dots\)といった無限小数はどのように定義されているか明確ではない
- 無限小数\(0.333\dots\)に3をかけると、その各桁に3をかけた無限小数になる根拠がない
もやもやとして納得しがたいのは、「小数が無限に続くってどういうこと?」、「そもそも\(0.999\dots\)とは何なのか?」をはっきりと決めていない部分にあるのです。
無限小数と数列、その極限について
そこで高校数学で学ぶ、数列の考え方を導入します。
\(a_n := \frac{9}{10^n}\) により定まる数列\(\{a_n\}_{n\in \mathbb{N}}\)を考えましょう。その第1項は\(a_1 =\frac{9}{10}=0.9\)、第2項は\(a_n = \frac{9}{100}= 0.09\)といったように続いていますね。この数列は、どのような\(n\)に対しても値を持っている、無限数列です。
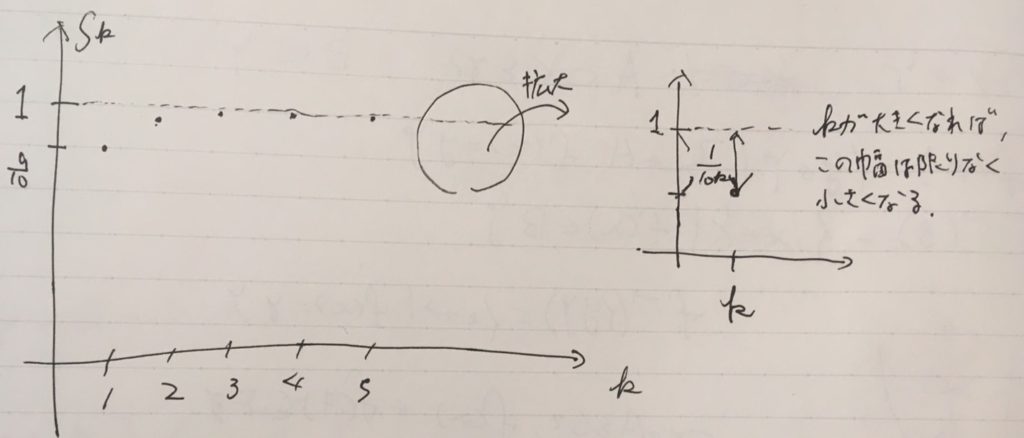
さらに、その第\(k\)項までの和(により定まる数列)を\[ \begin{aligned}S_k := a_1 +a_2 +\cdots + a_k= \sum _{i=1} ^k \frac{9}{10^i} \end{aligned} \]と定めます。\(S_1 =0.9,S_2 =0.99,S_3=0.999\)といった具合に、小数第\(k\)桁まで9が続く数列です。
\(S_{100}\)ならば、\(0.999\dots 99\)と100個の9が続いています。\(S_k \)において\(k\)がどんどん大きくなっていけば、無限小数\(0.999\dots \)を表現できていそうです。そこで、\(k\)が大きくなっていくときに\(S_k\)が近づいていく値を無限小数
\[ \begin{aligned}0.999\dots := \lim _{k\to \infty} S_k \end{aligned} \]
と定義します。右辺は、\(S_k\)の\(k\to \infty\)における極限(無限級数)です。
「無限小数とは何か」という問題を、数列と極限の言葉(高校数学)によって定義できました。
高校数学における極限は、「数列\(\{S_k\}\)において、項の番号\(k\)が限りなく大きくなっていくとき、\(S_k\)がある一定の値\(\alpha\)に近づいていくとき、数列\(\{S_k\}\)は収束すると言い、\(\lim S_k = \alpha\)と書く。」と定義されています。
今回定義した\(S_k\)が\(k\to \infty \)で\(1\)に収束することを証明しましょう。
まず、(\(k=2\)のとき)\(0.99 =\frac{99}{100} =1- \frac{1}{100}\)といったように捉え直します。一般には、
\[ \begin{aligned} S_k &= \sum_ {i=1} ^{k} \frac{9}{10^i}\\
&= 1- \frac{1}{10^k}\end{aligned} \]
が成り立ちます(等比数列の和の公式)。ここで、\(k\)が限りなく大きくなっていくときに、\(- \frac{1}{10^k}\)は限りなく0に近づくので、両辺は1に収束します。
よって、\(0.999\dots = \lim _{k\to \infty} S_k = 1\)が示せました。
- 「無限小数0.999…とは何か?」→「小数第\(k\)桁までの有限小数\(S_k=0.99\dots 9\)の\(k\to \infty\)における極限値」と定義
- その極限値が1であることを示す
という手順を踏みました。
途中の計算で見たように、1と有限小数\(S_k=0.99\dots 9\)の差は、たったの\( \frac{1}{10^k}\)です。この量は、\(k\)が大きくなればいくらでも0に近づきます。\(0.999\dots =1\)という式の意味は、有限小数の桁\(k\)を増やせばそれは限りなく1に近づきますよ、という意味だったわけです。
0.999…といった無限小数がどこまで行っても1より小さく見えるという感覚は、常に\(S_k <1\)が成り立つことに対応しています。どんな有限の\(k\)でも\(S_k<1\)ですが、その限りなく近づく値=極限値としては\(\lim _{k\to \infty} S_k =1\)が成り立つわけです。\(b_k:=\frac{1}{10^k}\)とすると、\(b_k \neq 0\)ですが、\(\lim_{k\to \infty} b_ k =0\)です。極限値とは限りなく近づく数値のことであり、その途中でピッタリ値を取らなくて良いことに注意しましょう。
ここまで来れば納得していただけたでしょうか。
数列の極限の定義における「限りなく近づく」部分にも、曖昧さを感じる人がいるかもしれません。良い目のつけどころです。数列の極限は、大学数学で(イプシロン-エヌ論法によって)明確に定義されます。また、\(\frac{1}{10^k} \to 0\)の証明には、「どんな実数に対してもそれよりも大きい自然数が存在する」アルキメデスの性質と呼ばれる実数の性質(実数の定義:公理)を用いています。これらについては別記事で紹介するかもしれません。
もし数列や極限といった言葉に馴染みがなければ、高校数学のその部分を勉強してみてください。さらに知りたい人は、大学の微積分・解析学の教科書を読むと良いでしょう。「無限」が関係する数学は、慎重にならないと意味がわからなくなってしまいますが、正確に扱えるようになれば豊かな世界が広がっているのが感じられると思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170