どうも、木村(@kimu3_slime)です。
平面内の曲線や2変数関数のグラフなど、多変数関数を理解するためにはそれを視覚化することがひとつの手がかりになります。
今回は、ベクトル値関数を理解するための方法として、それをベクトル場として描く方法を紹介します。また、ヤコビ行列を使ってベクトル場を線形化できることも紹介します。
実数のベクトルに関する前提知識:集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える、実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
ベクトル値関数の視覚化とベクトル場
2変数関数とは、\(f(x,y)=xy\)のように、2つの実数\(x,y\)により実数\(f(x,y)\)が決まる対応\(f:\mathbb{R}^2 \to \mathbb{R}\)のことでした。
ベクトル値関数(vector valued function)は、\(F(x,y)=(x,y)\)のように、取りうる値が(2次元以上の)ベクトルとなる関数です。単にベクトル関数とも呼ばれます。\(N\)変数で\(M\)次元のベクトルの値を取るならば、\(F:\mathbb{R}^N \to \mathbb{R}^M\)です。1変数で2次元のベクトル値ならば平面曲線、2変数で3次元のベクトル値ならば空間曲線を表すと考えられます。
今回主に考えたいのは、単純なケース、2変数で2次元のベクトル値関数です。\(F(x,y)=(F_1(x,y),F_2(x,y))\)と成分表示することができ、2つの2変数関数を同時に定めているとも見れますね。
2変数関数\(f\)の場合は、\((x,y,f(x,y))\in \mathbb{R}^3\)と、3次元空間内にグラフを描くことができました。2変数2次元ベクトル値関数の場合はどうでしょうか? \((x,y,F_1(x,y),F_2(x,y))\)を考えると、これは4次元必要になり、視覚的に描くことはできません。
ひとつの描写方法は、それを図形や座標の変換として捉える方法です。線形変換や極座標変換が典型例で、画像の変換の話は紹介しました。
もうひとつの描写方法が、ベクトル場として図示する方法です。ベクトルの対応関係を、矢印として空間に重ねて描きます。今回はこれを見ていきましょう。
線形ベクトル場
最初に簡単な例から考えていきましょう。
\(F(x,y)=(x,y)\)のベクトル場を描いてみます。まず\(x,y\)平面を取りましょう。その上に、\(F\)によって決まるベクトルを描いていきましょう。例えば、点\((1,1)\)には\((1,1)\)ベクトルに対応する矢印を描きます。いくつも描いていけば、原点から外側に放射状に向き、かつ原点から離れた場所では大きな矢印となることがわかるでしょう。これを図示したのが次の画像です。
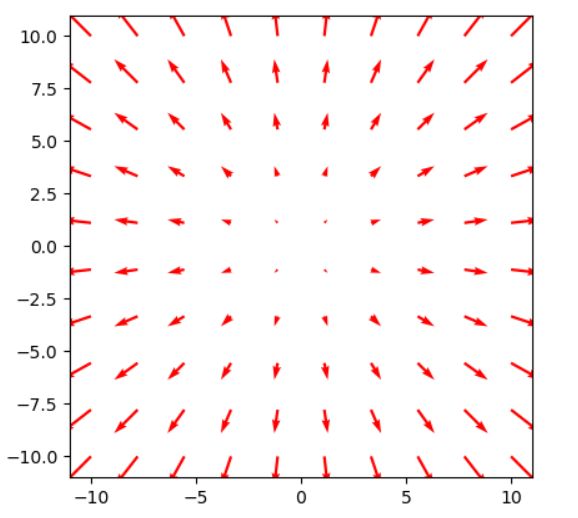
ベクトル場は、風や電気・磁気、水などの流れ(flow)を表していると解釈でき、物理学においてよく使われてきました。矢印をなめらかにつなぐと、次のような流れが見て取れます。
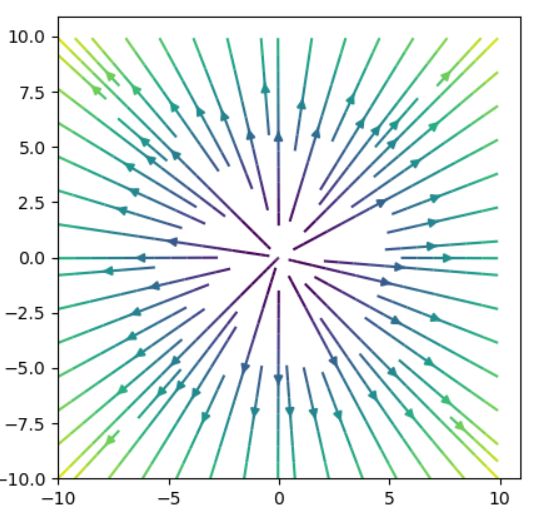
このベクトル場において、矢印は速度を表すもの、すなわち速度場として捉えてみましょう。色が暗い部分はゆっくりと、明るい部分は速く動いています。この図の場合は、原点を頂点とした球体で、頂点付近から出発してゆっくりと動き出して、やがて加速されていくようすが読み取れます。
このベクトル場の正負を逆にしてみましょう。\(F(x,y)=(-x,-y)\)です。矢印はすべて逆になり、原点に吸い込まれる形になりますね。

もっと別のベクトル場を考えてみましょう。
\[ \begin{aligned}F(x,y)= \begin{pmatrix} a&b\\c&d \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} ax+by\\cx+dy \end{pmatrix}\end{aligned} \]
と行列によって表されるベクトル場を、一般に線形ベクトル場といいます。
\[ \begin{aligned}F(x,y)=\begin{pmatrix} 0&1\\1&0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} y\\x \end{pmatrix}\end{aligned} \]
というベクトル場を考えてみます。\((1,1)\)を\((1,1)\)へ、\((1,-1)\)を\(-(1,-1)\)へと移すので、そのベクトルの方向には直線ができあがるのがわかりますね。
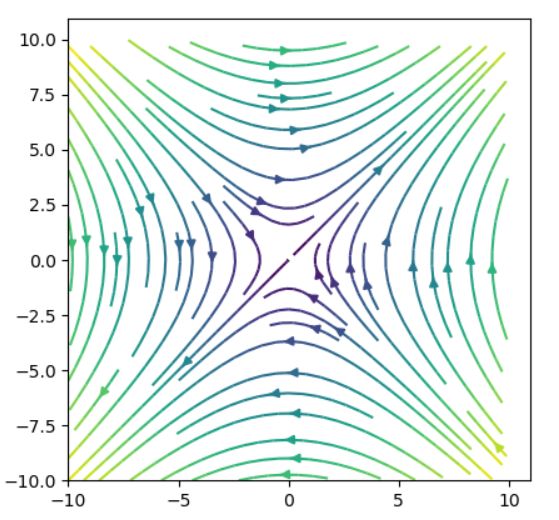
これらの特殊なベクトルは、行列の固有ベクトルです。原点に入り込む方向と、離れていく方向の2つがありますね。
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる
別の例です。
\[ \begin{aligned}F(x,y)=\begin{pmatrix} 0&1\\-1&0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} y\\-x \end{pmatrix}\end{aligned} \]
これは時計回りに90度の回転行列の定めるベクトル場です。
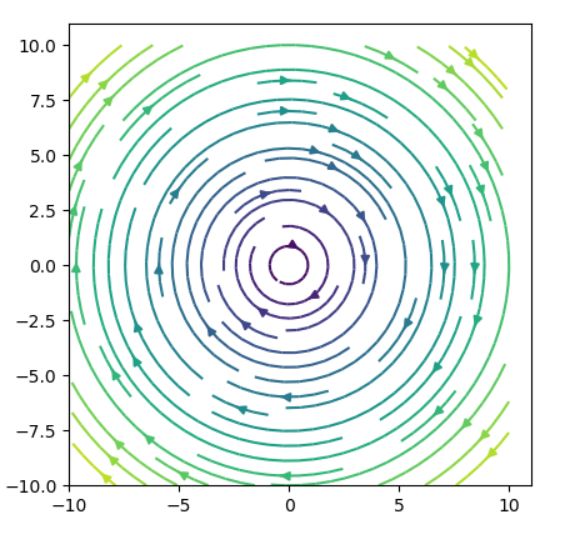
さらに別の例を。
\[ \begin{aligned}F(x,y)=\begin{pmatrix} -1&1\\-1&-1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} -x+y\\-x-y \end{pmatrix}\end{aligned} \]
これは
\[ \begin{aligned}F(x,y)=\begin{pmatrix} -x+y\\-x-y \end{pmatrix}=\begin{pmatrix} -x\\-y \end{pmatrix} +\begin{pmatrix} y\\-x \end{pmatrix}\end{aligned} \]
と、吸い込むベクトル場と回転するベクトル場の足し合わせとして解釈できますね。
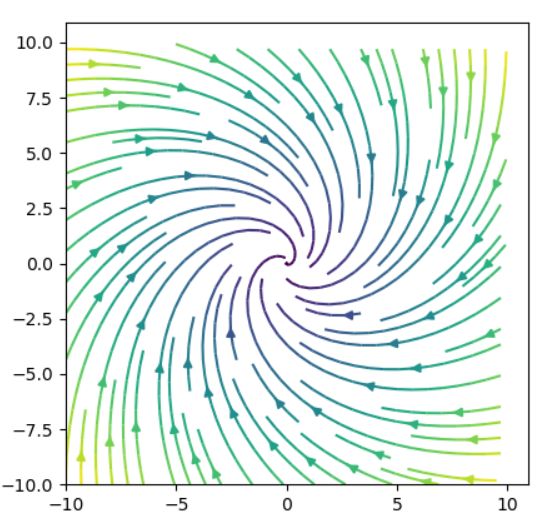
これまでに登場してきた、ベクトル場の矢印をつないでできあがる曲線を、ベクトル場の積分曲線(integral curve)と呼びます。文脈によって、解軌道、流線などとも呼ばれます。
ヤコビ行列と線形近似
さて、一般のベクトル場は線形とは限りません(非線形)。非線形ベクトル場を描くのは、線形ベクトル場と比べて難しくなります。
例えば、\(F(x,y)=(y,-\sin x)\)というベクトル場を考えてみましょう。これは単振り子の運動方程式から導かれます。
このベクトル場はどうやって描けば良いでしょうか。まず注目すべきは、いくつか止まっている(ベクトルの大きさが0)点です。\(F(x,y)=(0,0)\)を満たす点を、ベクトル場の平衡点(equilibrium point)と呼びます。
\((-\pi,0),(0,0),(\pi,0)\)などが平衡点です。これらの点を基準に、その周りのベクトル場を描いていくことで、次のような図ができるのではないでしょうか。
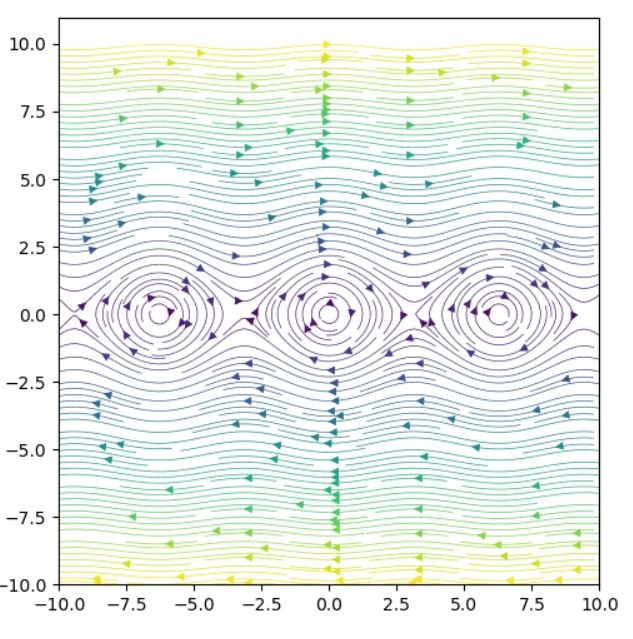
このベクトル場を、線形近似という視点から分析してみましょう。
1変数関数や2変数関数は、接線や接平面といった線形関数によって近似することができました。一般のベクトル場も、線形ベクトル場によって近似することができます。
次の行列によって決まる線形ベクトル場を考えてみましょう。ベクトル値関数の各偏微分を並べたものです。
\[ \begin{aligned} G(x,y) &= J_F(x,y)\\&:= \begin{pmatrix} \frac{\partial F_1}{\partial x}(x,y) & \frac{\partial F_1}{\partial y}(x,y) \\ \frac{\partial F_2}{\partial x}(x,y) &\frac{\partial F_2}{\partial y}(x,y) \end{pmatrix} \end{aligned} \]
この行列\(J_F\)を、\(F\)のヤコビ行列(Jacobi matrix)と言います。ヤコビ行列は多変数ベクトル値関数の一次近似です。そして、平衡点の付近で元のベクトル場をよく近似します。
今回の\(F\)ならば、 \(J_F(x,y)=\begin{pmatrix} 0&1\\ -\cos x &0\end{pmatrix}\)です。
したがって、\(J_F(0,0)=\begin{pmatrix} 0&1\\ -1 &0\end{pmatrix}\)で回転するベクトル場、\(J_F(0,\pi)=\begin{pmatrix} 0&1\\ 1 &0\end{pmatrix}\)で引き寄せと反発の合わさるベクトル場であることがわかります。
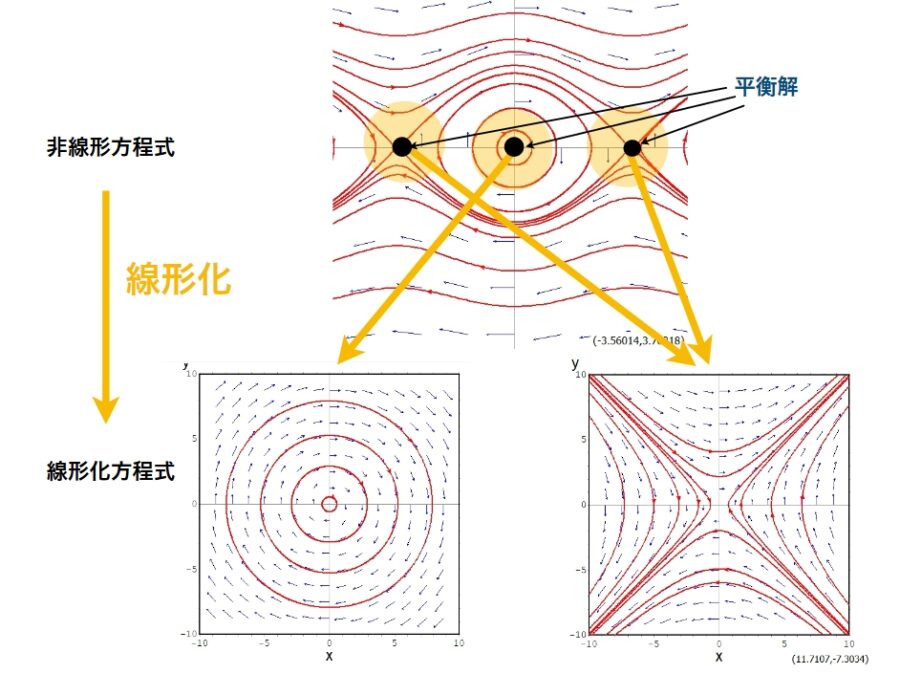
一般のベクトル場は、平衡点の付近で線形ベクトル場によって近似できます。多変数ベクトル値関数の偏微分、ヤコビ行列の考え方が役立っているのを感じられるでしょうか。
3次元のベクトル場
今回紹介したのは2次元のベクトル場でしたが、3次元のベクトル場も空間に図示することができます。
\(F(x,y,z)=(-x/r^3,-y/r^3,-z/r^3)\),\(r=\sqrt{x^2+y^2+z^2}\)なるベクトル場を考えます。これは、原点にある物体が周囲の点に及ぼす万有引力です。
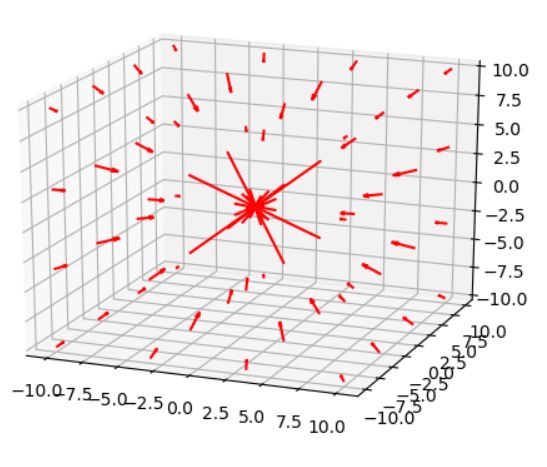
原点から遠い点では及ぶ力は弱いですが、原点に近づくほどその力は強くなりますね。空間的に、どの点であってもその中心側へ力が向かっているのがわかります。
今回は、2、3次元のベクトル場を考えましたが、曲線や曲面、より一般に多様体におけるベクトル場を考えることができます。多様体におけるベクトル場は、単にベクトル(\(n\)個の数)を対応させるというよりは、接ベクトルを対応させるものとして定義されます。
ベクトル場(やそれを拡張したテンソル場)は、重力や電磁気学、流体力学、相対性理論など、物理学において広く利用されています。
数学では、微積分学において特にベクトル場の微積分を扱う分野は、ベクトル解析(vector analysis)と呼ばれ、理工系の数学の基礎となっています。ベクトル解析の用語は、時空間上の状態変化を記述する偏微分方程式(partial differential equation)の基礎です。また、ベクトル場によって定まる微分方程式系の、解の挙動を調べる理論は、力学系理論(dynamical systems theory)として知られるものです。
はじめに紹介したように、ベクトル値関数は、ベクトル場としてだけでなく、座標変換として見ることもできます。ただ、「それは空間にどんな矢印を描いているだろうか?」というベクトル場の視点を持つと、ベクトル値関数やベクトル解析の理論が視覚的に理解しやすくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門