どうも、木村(@kimu3_slime)です。
前回、力学系理論の入門として、解の安定性の話を紹介しました。
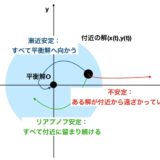
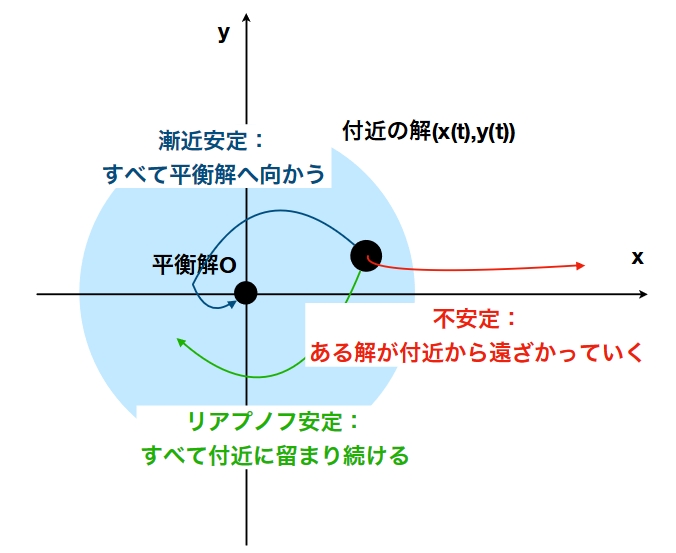
平衡解と呼ばれる時間変化しない解の安定性は、その付近の解のふるまいによって分別されます。「離れていかない」リアプノフ安定、「近づいていく」漸近安定、「離れていく」不安定と。
今回は、その安定性が「固有値」を調べることによって判別できるという話を紹介します。
なぜ線形代数学で固有値の話を学ぶのか、その応用例のひとつでもあります。
線形方程式とは
今回考える常微分方程式は、シンプルな方程式、線形方程式です。\(x\in\mathbb{R}^N\)、\(A\)を\(N\times N\)の行列として
\[ \begin{aligned}\frac{dx}{dt}= Ax\end{aligned} \]
と表せる方程式を線形方程式と言います。\(x=0\)は平衡解となっていますね。
例をいくつか見てみましょう。前回紹介したバネの運動方程式は
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-x \end{array} \right.\end{aligned} \]
でしたが、これは
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
と表せます。(左辺は\(x=(x,y)^T\)と表記していることに注意)
ほかにも、次のように書き直すことができます。
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-x+y \\ \frac{dy}{dt} =-x-y \end{array} \right.\end{aligned} \]
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} -1 & 1 \\ -1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} = x \end{array} \right.\end{aligned} \]
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0& 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
線形でない方程式はいくらでもあり、例えば振り子の運動方程式
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =- \sin x \end{array} \right.\end{aligned} \]
は線形方程式ではありません(非線形方程式)。
固有値によって安定性を判別する
さて、線形方程式の行列\(A\)の固有値を調べることによって、平衡解\(0\)の安定性を調べることができます。
行列は、点\((x,y)\)を別の点へ移す変換とみなせます(相図でいう矢印)。その変換はどのような性質なのかを調べるのが、固有値です。
\[ \begin{aligned}A\phi =\lambda \phi ,\phi \in \mathbb{C}^N,\phi\neq 0\end{aligned} \]
を満たす\(\lambda\in \mathbb{C}\)を固有値(eigenvalue)、\(\phi\)を\(\lambda\)に対応する固有ベクトル(eigenvector)と呼びます。
実例を見てみましょう。
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
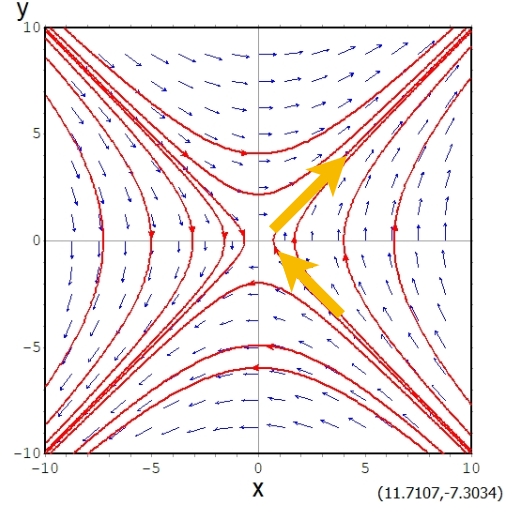
行列の固有値は\(\lambda = 1,-1\)、固有ベクトルは\((1,1),(1,-1)\)です。
対応する相図に、固有ベクトルを黄色く図示してみました。青い矢印がゆがまずに伸びている方向が固有ベクトルです。
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} -1 & 1 \\ -1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
に対しては、固有値は\(\lambda = -1+i,-1-i\)、固有ベクトルは\((1,i),(1,-i)\)です。
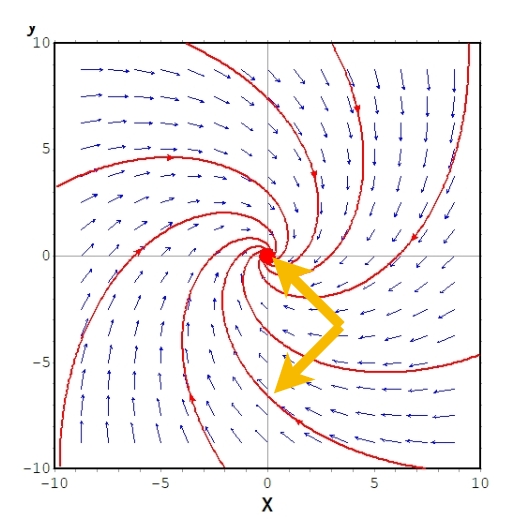
黄色は固有ベクトルではありませんが、イメージとして示しました。固有値に虚数部分があるとき、それは回転として解釈できます。
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
これは固有値\(\lambda =i,-i\)、固有ベクトルは\((1,i),(1,-i)\)です。
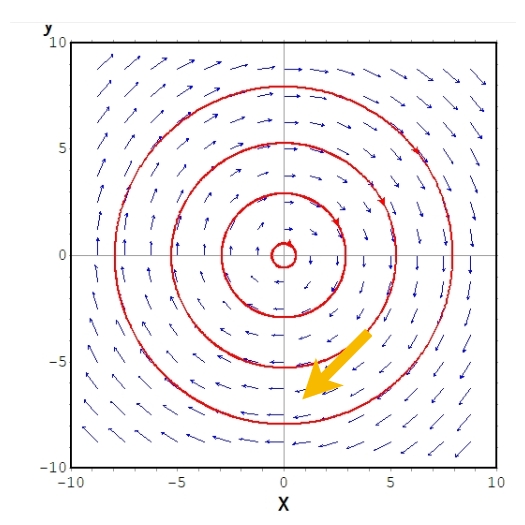
固有値と方程式の安定性に関する情報をまとめてみましょう。
固有値\(\lambda =i,-i\)の方程式は、リアプノフ安定
固有値\(\lambda = -1+i,-1-i\)の方程式は、漸近安定
固有値は\(\lambda = 1,-1\)の方程式は、不安定
じつは、固有値の実部の正負によって方程式の安定性を判別できます。
定理
固有値の実部がすべて非正ならば、リアプノフ安定
固有値の実部がすべて負ならば、漸近安定
ある固有値の実部が正ならば、不安定
この定理はここでは証明しません。ウィギンス「非線形の力学系とカオス」参照。
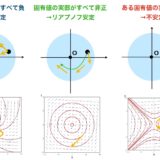
今まで紹介してきた例、固有値による安定性判別の方法を図にまとめてみました。
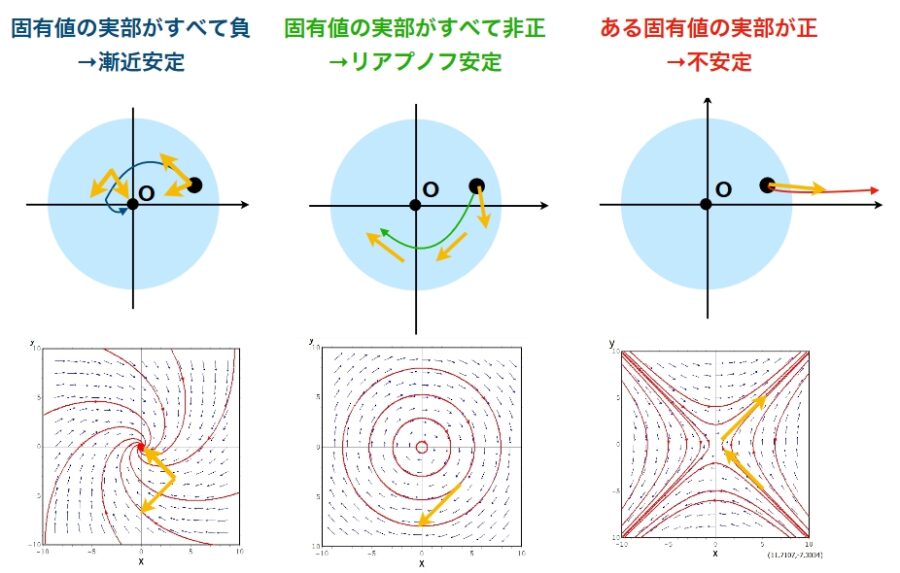
左側の図の固有値は\(\lambda = -1+i,-1-i\)で、実部はどちらも\(-1\)。これは解を中心(平衡解)へ動かす力が働くことを意味します。
真ん中の図の固有値は\(\lambda = i,-i\)で、実部はどちらも0。これは解を中心へ引き込みもしないし、外側へ飛ばしもしないということです。
右の図の固有値は\(\lambda = 1,-1\)。ある方向では引き込んでいます。しかし、別のある方向では外側へ飛ばしています。
3つの例を見比べると、虚数を含む固有値の図は、回転変換が起こっていることがわかります。固有値の虚部は回転を示すもので、方程式の安定性には関係がありません。
安定性に関係してくるのは、固有値の実部の正負です。方程式の解は、実部が負ならば内側へ、正ならば外側へ解が動いていきます。つまり、全方向で内側に引き込むなら漸近安定、ある方向で外側へ飛ばすなら不安定ですね。
今回は、線形な方程式を考え、その平衡解の安定性を固有値によって判別する方法を紹介しました。
より一般の方程式、非線形方程式でも安定性を判別することはできないのでしょうか?
じつは、非線形方程式を「線形化」することで、今回の判別法に帰着させられます。その話はまた別の記事で紹介する予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京
売り上げランキング: 1,154,556
朝倉書店
売り上げランキング: 372,923
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ
カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に