どうも、木村(@kimu3_slime)です。
物理現象が数学的なルールで決まっているなら、コンピューターで未来をすべて予測できるんじゃないの? いやいや、実はそうでもないんです。コンピューターの能力の問題ではなく、予測しにくい現象があります。
今回は、カオス理論、バタフライ・エフェクトについて簡単に紹介したいと思います。
カオス理論とは
カオス理論とは、ほんのわずかに初期条件が変わるだけで結果に大きな差が起こる現象、予想がつかないような複雑な現象を起こす微分方程式・力学系を扱う理論のことです。
カオスは、英語で混沌、無秩序を意味しています。
ローレンツ方程式、ローレンツ・アトラクター
カオス現象の具体例を見てみましょう。
気象学者のローレンツ(Lorenz)は、大気の変動モデルを研究していました。
本来はナビエ・ストークス方程式という非線形の偏微分方程式によって大気変動は説明されますが、それをめちゃくちゃ単純化し、3成分の常微分方程式と変形させ、数値計算を行ってみたのです。
\[\left\{ \begin{array}{l} \frac{dx}{dt} = -ax +ay \\ \frac{dy}{dt} = -xz + bx -y \\ \frac{dz}{dt} = xy – cz \end{array} \right.\]
このモデルはもはや現実と対応していませんが、例えば\(x,y,z\)の3成分を、気温、湿度、風の強さと考え、気象現象を表すとみなすこともできます。
ローレンツは、パラメータを\(a = 10、b = 28、c = 8/3\)としたときに、実に複雑な気象現象が起こることを発見しました。

画像引用:Chaos7 Attracteurs étranges : L’effet papillon
この結果は、「Deterministic Nonperiodic Flow(決定論的で非周期的な流れ)」という論文で発表されました。
上の画像に示されているように、あらゆる気象現象は、チョウチョの羽のような2つの輪っかへと引き込まれていきます。
一般に、力学系理論では、周囲の状態を引き寄せる集合のことを、アトラクター(attractor)と言います。
ローレンツの発見したアトラクターは、ローレンツ・アトラクター、またはストレンジ・アトラクターと呼ばれます。まさに奇妙なアトラクターです。
バタフライ・エフェクトとは
ローレンツは、その研究を講演で話す予定でしたが、会議の主催者が急いでいたため、勝手にそのタイトルをつけてしまいました。
Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”
(予測可能性:ブラジルの1匹の蝶の羽ばたきはテキサスで竜巻を引き起こすか?)
ちょっとしたチョウチョの羽ばたきが、地球の裏側で竜巻を引き起こすかもしれない……。これはバタフライ・エフェクトと呼ばれます。
ローレンツはそこまでは言っていませんが、この表現は詩的で人気となり、数学だけでなく一般に盛り上がっていく話題となりました。
「人間は運命から逃れられるか?」という運命論と結び付けられ、多くのドラマや映画の題材となっています。「バタフライ・エフェクト」という映画もありますし、想定科学アドベンチャー「STEINS;GATE(シュタインズゲート)」ではよくチョウチョのモチーフが登場します。
カオス、初期値鋭敏性とは
カオスには、いくつかの定義があります。
その中で有名な定義が、初期状態に対する鋭敏性(sensitivity)です。
多くの物理法則、微分方程式では、同じ初期状態が同じ結果を生み出すだけではなく、似ている初期状態は似ている結果を生み出します。これは初期状態に関する連続性(continuity)と言われます。
ローレンツの方程式、カオス現象では、似ている初期状態から始まっても大きく異なる結果を生み出します。
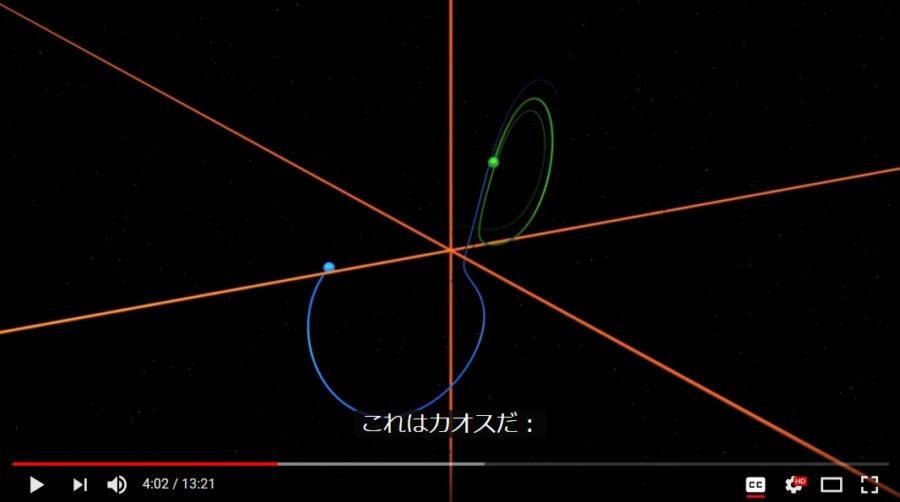
画像引用:Chaos7 Attracteurs étranges : L’effet papillon
ローレンツの方程式は、めちゃくちゃな方程式ではありません。同じ初期状態が同じ結果をもたらす、決定論的なものです。にもかかわらず、少し初期状態が違うだけで大きな違いを生み出してしまうんですね。
現実の気象現象にどこまでカオス現象が起こっているかは不明ですが、ローレンツの単純化した方程式ですら起こっていることが、より変数をたくさん持ち現実にマッチした方程式や、現実に起こらないとは言えないでしょう。
カオスというキーワードは、数学に詳しくない一般の人でも楽しみやすいものです。
Jos Leys, Étienne Ghys, Aurélien Alvarezによって作られたハイクオリティな3Dビデオ「CHAOS」は、カオス理論入門としておすすめです!
この動画を紹介するために、この記事を書いたと言っても過言ではない(笑)。しかも無料ですからね。ぜひ、現象の予測とカオスの世界に踏み込んでいってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
バタフライ・エフェクト プレミアム・エディション [DVD]
売り上げランキング: 16,683
こちらもおすすめ
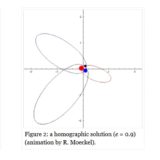
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ
ローレンツアトラクター以外のカオスの具体例を紹介する記事を書きました:カオス現象のわかりやすい具体例を視覚的に見る

![バタフライ・エフェクト プレミアム・エディション [DVD]](https://images-fe.ssl-images-amazon.com/images/I/515Qf4g7%2BiL._SL160_.jpg)