どうも、木村(@kimu3_slime)です。
前回は、線形な微分方程式の安定性を固有値によって判別する方法を紹介しました。
より一般の方程式、非線形方程式の安定性を調べるにはどうしたらよいのでしょうか。
今回は、線形化の方法と呼ばれる調べ方を紹介します。
方程式の線形化とは
非線形方程式の例として、単振り子の運動方程式を考えてみます。それは
\[ \begin{aligned} \left\{\begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-\sin x \end{array} \right.\end{aligned} \]
となります。ここで\(x\)は振り子が重力の方向となす角です。(参考:単振り子 : 運動方程式 (equation of motion) – KIT 物理ナビゲーション)
\(\sin x\)が非線形項であり、方程式を行列(線形関数)によって表すことができません。(このような方程式を、一般に非線形方程式と言います。)
この方程式には、\((0,0)\)だけでなく、\((\pi,0),(2\pi,0)\)といった平衡解があります。
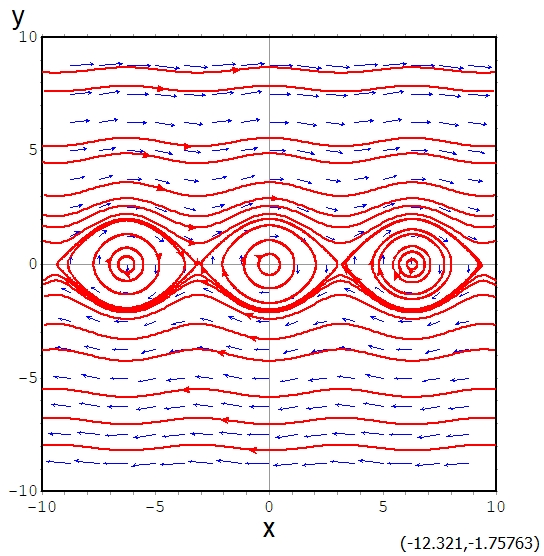
これからは平衡解を\(\bar{x}=(\bar{x},\bar{y})\)と表すことにします。
平衡解\(\bar{x}\)のまわりで非線形項\(\sin{x}\)をテイラー展開(多項式展開)してみましょう。(テイラー展開は大学1年の微積分で習う重要な話のひとつ)
\[ \begin{aligned}\sin x = \sin(\bar{x})+\cos(\bar{x})(x-\bar{x}) -\frac{1}{3!}\cos(\bar{x})(x-\bar{x})^3+\cdots\end{aligned} \]
ここで\(x\)が\(\bar{x}\)に近いとき、3次\((x-\bar{x})^3\)以降の項は(1次の項と比べると)十分小さいとみなせます。また、\(\bar{x}\)は平衡点なので、\(\sin(\bar{x})=0\)です。これをもとの式に戻すと
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-\cos(\bar{x})(x-\bar{x}) \end{array} \right.\end{aligned} \]
\(\bar{x}=(0,0)\)のときは
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
\(\bar{x}=(\pi,0)\)のときは
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x-\bar{x} \\ y \end{pmatrix}\end{aligned} \]
となります。ちゃんと線形の方程式が得られましたね。これを\(\bar{x}\)における線形化方程式と言います。
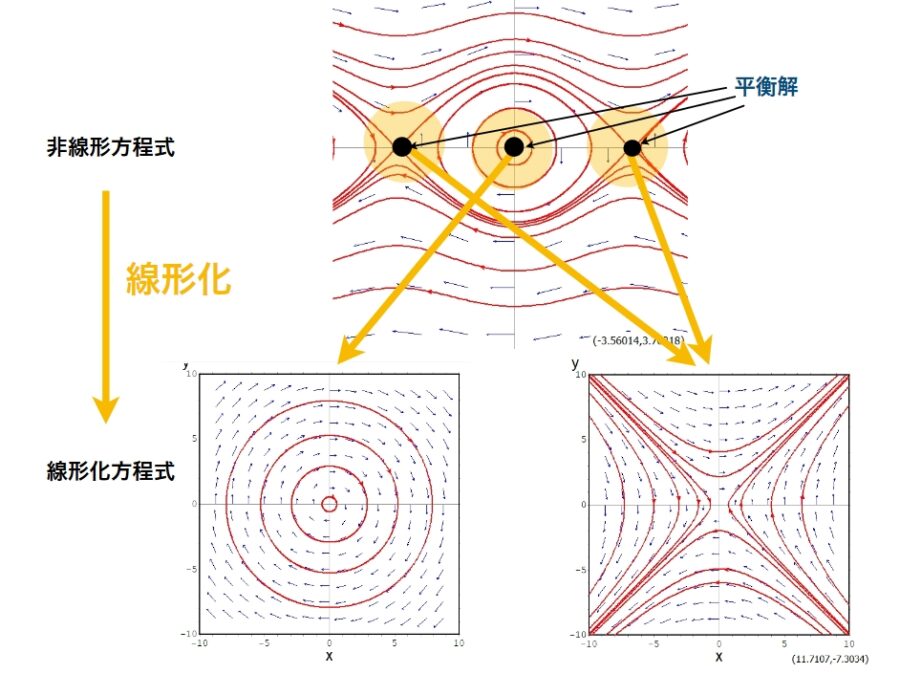
それぞれの平衡点における線形化方程式の相図を書くと上のようになります。非線形方程式の平衡点のまわりを虫眼鏡で拡大したような図になっていますね。
つまり、線形化とは局所的な近似であるということができます。
より一般に、(非線形の)関数\(f(x)\)によって定まる微分方程式系
\[ \begin{aligned}\frac{dx}{dt}= f(x)\end{aligned} \]
の\(\bar{x}\)における線形化は、
\[ \begin{aligned} \frac{dx}{dt}&= J_f(\bar{x}) \begin{pmatrix} x \\ y \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial f_1}{\partial x}(\bar{x}) & \frac{\partial f_1}{\partial y}(\bar{x}) \\ \frac{\partial f_2}{\partial x}(\bar{x}) & \frac{\partial f_2}{\partial y}(\bar{x}) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
となります。ここで\(J_f\)はヤコビ行列(Jacobian)と呼ばれる行列です。ヤコビ行列は、多変数の微積分学に登場する重要な行列で、多変数関数の「接平面」を与える「微分係数」の一般化ですね。
参考:2変数関数と偏微分:グラフ、接平面を描いてみよう、ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
方程式の不安定性は線形化方程式からわかる
さて、知りたいのは非線形方程式の安定性でした。これは線形化方程式の安定性とどのような関係にあるのでしょうか。次のことが知られています。
定理
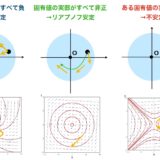
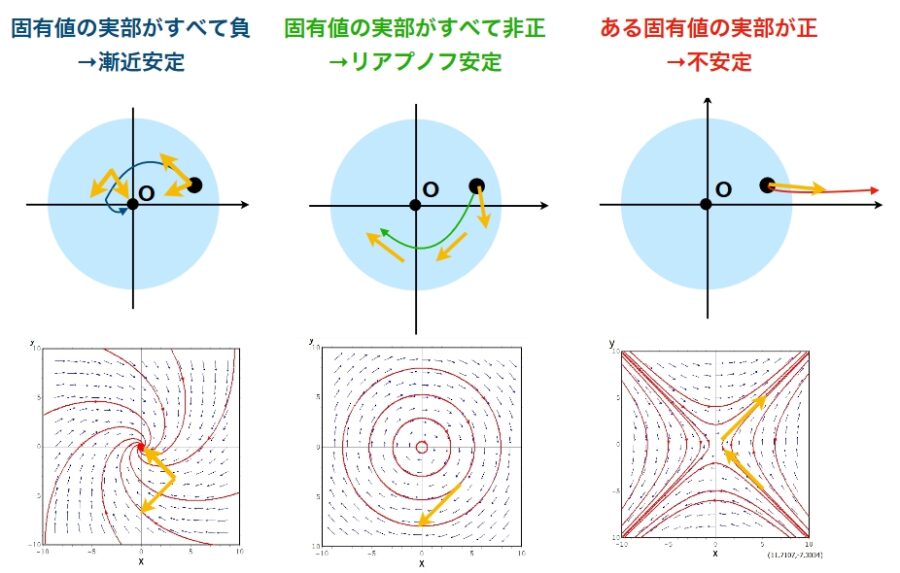
平衡点\(\bar{x}\)において、線形化方程式の行列の固有値を考えます。すべての固有値が負の実部を持つならば、もとの非線形方程式は漸近安定です。
(証明はリアプノフ関数というものを使います、ウィギンス「非線形の力学系とカオス」を参照。)
また、ある固有値が正の実部を持ち、すべての固有値の実部が0でない(双曲型不動点)ならば、もとの非線形方程式は不安定です。(ハートマン・グロブマンの定理)
前回紹介した固有値による判別法に似たものが、そのまま成り立つというわけです。
減衰を考慮した振り子の方程式
\[ \begin{aligned} \left\{\begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-\sin x -y \end{array} \right.\end{aligned} \]
の平衡点\((0,0)\)については、線形化行列が
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & 1 \\ -1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
で、固有値が\(\lambda=-\frac{1}{2} \pm \sqrt{3}i\)となり、すべて実部が負なので、定理より元の方程式の平衡点は漸近安定です。
しかし、リアプノフ安定性や不安定性は、この定理からはわかりません。
(振り子の運動方程式の場合は、リアプノフ関数という方法を使うと、\(\bar{x}=(0,0)\)のリアプノフ安定性が示せます。)
線形化の方法では安定性がわからない例
じつは、線形化した方程式の挙動は、もとの方程式の挙動と一致しないことがあります。次のことを問うてみましょう。
問題
平衡点\(\bar{x}\)において、線形化方程式の行列の固有値を考えます。
すべての固有値が非正の実部を持つならば、もとの非線形方程式はリアプノフ安定と言えるか?
ある固有値が正ならば、不安定と言えるか?
答えはネガティブです。
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-y+x(x^2+y^2) \\ \frac{dy}{dt} =x +y(x^2+y^2) \end{array} \right.\end{aligned} \]
という方程式を考えてみましょう。\(\bar{x}=(0,0))\)は平衡点であり、線形化方程式は
\[ \begin{aligned}\frac{dx}{dt}= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\end{aligned} \]
となります。
固有値は\(\lambda=\pm i\)で、すべて非負の実部を持ちます。しかし、平衡点はリアプノフ安定ではなく、不安定です。
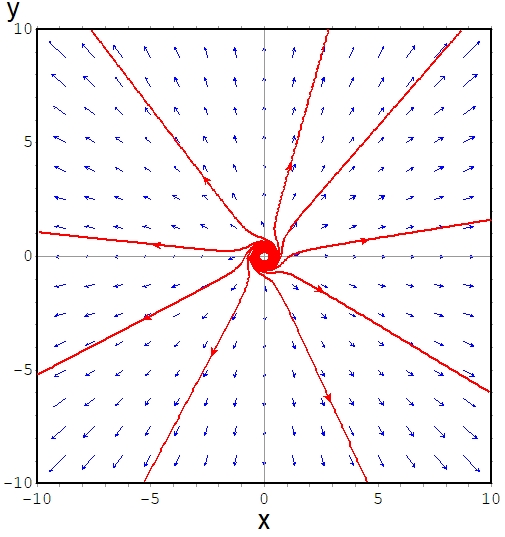
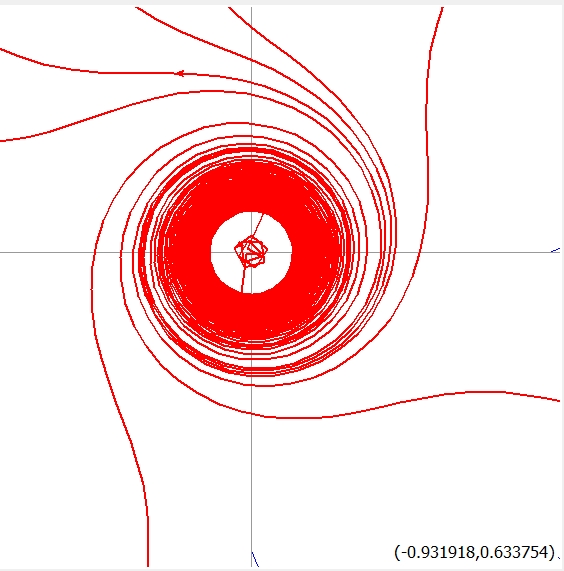
原点にどんなに近い解でも、うずをまきながら遠くへ飛んでいってしまいます。
数学では、「シンプルなケースで成り立っていた法則が、できるだけ一般に成立しないか?」という一般化の問題をよく考えます。例えば、線形の方程式における安定性判別が、非線形方程式でも使えないか考えたくなるものです。
しかしながら、今回の例は、非線形の方程式では別の判定法が必要となることを明らかにしてくれました。命題を否定する例は反例(counterexample)と呼ばます。反例は一般論の邪魔をしますが、面白い結果を生み出す源でもあるんですよね。反例探しは楽しいですよ。
おさらいをすると、線形化方程式の固有値がすべて負の実部を持つならば、もとの方程式が漸近安定であることを紹介しました。
では、固有値がすべて負の実部を持たないときはどうするか。すべてが簡単に判別できるわけではありませんが、リアプノフ関数という関数を使った判別法があります。また別の記事で紹介するかもしれません。
紹介しました→安定性を判別するリヤプノフ関数の方法とは?
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京
売り上げランキング: 1,154,556
共立出版
売り上げランキング: 427,579
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門