どうも、木村(@kimu3_slime)です。
今回は、2変数関数の極値の求め方、ヘッセ行列を使った判定法を、高校数学(1変数のケース)と比較しながら紹介していきます。
1変数関数の極値の判定方法
高校数学では、1変数関数の極値の求め方を学びました。
例えば\(f(x)=x^2\)において\(x=0\)は極小点であり、\(f(x)=-x^2\)において\(x=0\)は極大点です。
極値(extremum)とは、極大値(local maximum)と極小値(local minimum)の総称です。関数\(f\)が\(a\)で極大値を取るとは、\(a\)に十分に近い\(x\)について\(f(x)\leq f(a)\)が成り立つことです(極小なら符号が逆になる)。特に、定義域全体での極大値を最大値、極小値を最小値と言います。
極値を取る点では、関数の値が局所的に変化していない、つまり導関数が0となっています。
(ある程度なめらかな関数を考えるとき)
\(f\)が\(x=a\)で極値を取る\(\Rightarrow\) \(f^{\prime}(a)=0\) (\(a\)が臨界点)
極値を探すには、まず\(f^{\prime}(a)=0\)なる点\(a\)を探します。このように微分が0になる点は、臨界点(critical point)、停留点(stationary point)と呼ばれます。
ただし、すべての臨界点が極値点であるわけではありません。\(f(x)=x^3\)を考えると、\(f^{\prime} (0)=0\)なので\(x=0\)は臨界点ですが、極値点ではありません。\(x=0\)のどんなに小さな近傍を考えても、\(f(x)\)は正負の値を取ってしまいます。(こういう点を変曲点という)
そこで高校数学では、関数の増減表を書き、臨界点の前後で\(f^{\prime}(x)\)の符号が変化するかどうかを調べます。例えば、マイナスからプラスへ転じるならばそこは極小点です。\(f^{\prime}\)の変化は、その変化率である2階導関数\(f^{\prime \prime}\)の符号によってチェックできます。
\(x=a\)が臨界点かつ\(f^{\prime \prime}(a)<0\) \(\Rightarrow\) \(x=a\)は極大点
\(x=a\)が臨界点かつ\(f^{\prime \prime}(a)>0\) \(\Rightarrow\) \(x=a\)は極小点
\(f^{\prime \prime}(a)\)の符号を調べることで、\(f\)が\(x=a\)の付近で上に凸なのか、下に凸(凹)なのかが判別でき、極値の判定ができるわけです。ただし、\(f^{\prime\prime}(a)=0\)のケースは退化しており、極値であるともないとも言えず、さらなる考察が必要となります。
関数の局所的な変化を考察するには、テイラー展開が有効です。
\[ \begin{aligned}f(x) \simeq f(a) +f^{\prime}(a)(x-a) +\frac{1}{2} f^{\prime \prime} (a)(x-a)^2\end{aligned} \]
と\(x=a\)の付近では近似できますが、\(a\)が停留点ならば
\[ \begin{aligned}f(x) \simeq f(a) +\frac{1}{2} f^{\prime \prime} (a)(x-a)^2\end{aligned} \]
と実質2次関数になります。2次関数の極値は直観的に明らかであり、\(f^{\prime \prime} (a)\)の符号によって状況が変わるのがわかるでしょう。
簡単な2変数関数の極値
1変数関数の極値と同様にして、2変数関数\(f(x,y)\)の極値について考えてみます。
\(f_1(x,y)=x^2+y^2\)の極値はシンプルです。\(p_0 =(0,0)\)の付近において、常に\(f_1(p_0)=0\leq x^2+y^2=f_1(x,y)\)が成立するので、\(p=p_0\)は極小点です(最小値でもある)。
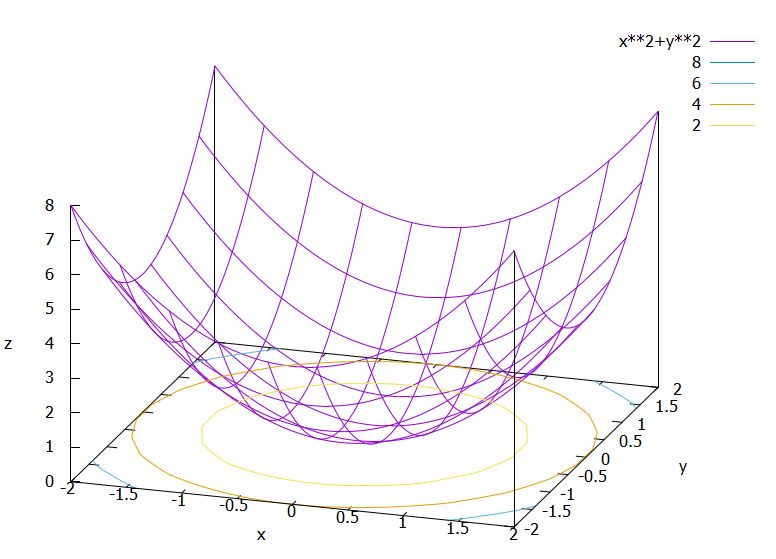
\(f_2(x,y)=-(x^2+y^2)\)について、同様に考えれば、\(p_0 =(0,0)\)は極大点(最大点)ですね。
2変数関数についても、同様に極値の定義をしています。
関数\(f(x,y)\)が\(p=p_0\)で極大値を取るとは、\(p_0\)に十分に近い\(p\)について\(f(p)\leq f(p_0)\)が成り立つことです(極小なら符号が逆になる)。
極値を取っているときは、少なくとも\(f(x,y)\)の\(x\)方向、\(y\)の変化率、つまり偏導関数\(f_x,f_y\)の値は0です。
\(f\)が\(p=p_0\)で極値を取る\(\Rightarrow\) \(f_x(p_0)=f_y(p_0)=0\) (\(p_0\)が臨界点)
\(\Leftrightarrow\)\(\nabla f (p_0)=0 \)
臨界点であることは、勾配ベクトル\(\nabla f =\mathrm{grad} f = (f_x,f_y)\)が0(ベクトル)になるとも言いかえられます。
2変数関数では、2次式を考えても極値を持たないことがあります。
\(f_3(x,y)= x^2 -y^2\)について考えます。\(p_0=(0,0)\)は臨界点であり、極値の候補です。しかし、極値点ではありません。
仮に極小点だったとしても、\(p=(0,y)\)の方向では\(f_3 (p)= -y^2 \leq 0=f_3 (p_0)\)と近くに値が下がる点が存在して、矛盾します。極大点と仮定しても同様です。
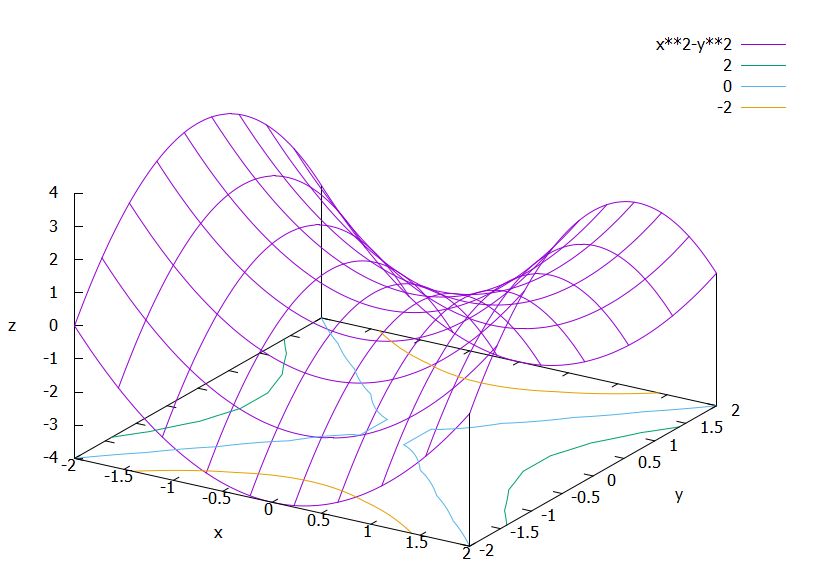
\(f_3\)の臨界点では、グラフは山の峠の形をしていて、ある方向に上り調子、ある方向に下り調子です。このような点\(p_0\)は、鞍点、サドル点(saddle point)と呼ばれます。
\(f_4(x,y)=xy\)においても、\(p_0=(0,0)\)は臨界点ではあるが、極値点ではありません。
2変数関数の極値の判定方法
今までの例を活かして、極値の一般的な判定方法を考えてみましょう。
2変数関数では、2階偏導関数は\(f_{xx},f_{xy}=f_{yx},f_{yy}\)と複数あります。1変数関数のように、1つの2階導関数の「符号」を見るだけでは判別できません。
しかし、似たような判別方法は成り立ちます。そのために、2階偏導関数をまとめた行列を考えましょう。
\[ \begin{aligned}H(f) = \begin{pmatrix} f_{xx} & f_{xy}\\f_{yx}&f_{yy} \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f) = f_{xx} f_{yy} – (f_{xy})^2\end{aligned} \]
この行列\(H(f)\)を\(f\)のヘッセ行列(Hessian matrix)、その行列式\(\det H(f)\)をヘッセ行列式、ヘッシアン(Hessian determinant)と呼びます。
\[ \begin{aligned}f(p)\simeq f(p_0)+\langle\nabla f,(p-p_0) \rangle \\ +\frac{1}{2}\langle (p-p_0) , H(f)(p-p_0) \rangle\end{aligned} \]
と表されるので、ヘッセ行列は1変数の2階偏導関数の一般化となっていると言えます。\(p_0\)が臨界点のときは、\(\nabla f (p_0)=0\)となるので、
\[ \begin{aligned}f(p)\simeq f(p_0)+\frac{1}{2}\langle (p-p_0) , H(f)(p-p_0) \rangle\end{aligned} \]
となって、\(f\)の挙動はヘッセ行列、その行列式に大きな影響を受けます。
具体例\(f_1(x,y)=x^2+y^2\)、\(f_2(x,y)=-(x^2+y^2)\)、\(f_3(x,y)= x^2 -y^2\)、\(f_4(x,y)=xy\)について、\(p_0=(0,0)\)におけるヘッセ行列、ヘッセ行列式を計算してみます。
\[ \begin{aligned}H(f_1) (p_0)= \begin{pmatrix} 2 & 0\\0&2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f_1) = 4\end{aligned} \]
\[ \begin{aligned}H(f_2) (p_0)= \begin{pmatrix}- 2 & 0\\0&-2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f_2) = 4\end{aligned} \]
\[ \begin{aligned}H(f_3) (p_0)= \begin{pmatrix} 2 & 0\\0&-2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f_3) = -4\end{aligned} \]
\[ \begin{aligned}H(f_4) (p_0)= \begin{pmatrix} 0 & 1\\1&0 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f_4) = -1\end{aligned} \]
極値点になるケースでは、行列式が正\[ \begin{aligned}\det H(f_1) >0,\det H(f_2) = 4\end{aligned} \]であり、極値点にならないケースでは、行列式が負\[ \begin{aligned}\det H(f_3) <0,\det H(f_4) <0\end{aligned} \]となっています。
証明は省略しますが、この関係は一般化されます。
\(f\)を\(C^2\)級の2変数関数で、\(p=p_0\)を臨界点とする。
- \(\det H(f) >0\)ならば、\(p=p_0\)は極値点である。
- \(f_{xx}<0\)ならば、\(p=p_0\)は極大点である。
- \(f_{xx}>0\)ならば、\(p=p_0\)は極小点である。
- \(\det H(f) <0\)ならば、\(p=p_0\)は極値点ではない。
\(g(x,y)=e^{-(x^2+y^2)}\)を例に、極値を判定してみましょう。
\(g_x = -2x g,g_y =-2y g\)なので、\(p_0=(0,0)\)が唯一の臨界点です。そこでのヘッセ行列、ヘッセ行列式は
\[ \begin{aligned}H(f_1) (p_0)= \begin{pmatrix} -2 & 0\\0&-2 \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}\det H(f_1) = 4\end{aligned} \]
です。よって、ヘッセ行列式が正であり、\(g_{xx}(p_0)<0\)なので、\(p=p_0\)は\(g\)の極大点で、極大値は\(g(p_0)=1\)と求められました。

テイラー展開によれば、2次の多項式\(f(p)=\langle (p-p_0) , H(f)(p-p_0)\rangle \)の挙動が重要です。一般にこのような多項式は2次形式と呼ばれ、線形代数や微積分でよく調べられています。
2次形式の係数は行列で表されますが(ここではヘッセ行列)、その行列が持つ性質によって、2次形式の値の性質が導き出せるのです。
2次形式が常に正になるような行列を、正定値行列と言います(負定値行列も同様)。正負どちらの値も取る時は、不定値行列と呼ばれます。すると、行列が正定値(負定値)であることは、その固有値がすべて正(負)であることと同値です。正負両方の固有値を持つときは、不定値です。
一般に、行列式は固有値の積に等しいです。したがって、サイズが2のときは、行列式が正ならば、固有値はすべて正かすべて負であり、定値行列です。また行列式が負ならば、固有値は正負混合であり、不定値行列です。おおざっぱに言えば、これが極値判定ができる理由です。
\(f\)を\(C^2\)級の関数で、\(p=p_0\)を臨界点とする。
- \(H(f)(p_0)\)の固有値がすべて負ならば、\(p=p_0\)は極大点である。
- \(H(f)(p_0)\)の固有値がすべて正ならば、\(p=p_0\)は極小点である。
- \(H(f)(p_0)\)が正負両方の固有値を持つならば、\(p=p_0\)は極値点ではない。
詳しくは:2次形式、正定値行列とは:2変数関数の極値判定を例に
以上、2変数関数の極値の求め方を、1変数のケース(高校数学)と比較しながら用語を整理し、紹介してきました。
極値の判定には2階偏導関数が重要ですが、2変数ではヘッセ行列、ヘッセ行列式に一般化されます。(多変数でも同様です)
原理はともかく、極値の判定条件自体は簡単なので、ぜひいろいろな2変数関数の極値を判定してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740