なぜ行列式を学ぶのか？固有値・固有ベクトルの求め方：固有多項式の定義

どうも、木村（@kimu3_slime）です。

線形代数学では、行列式というものを学びます。それは行列によって定まる数値ですが、一般的な定義は複雑な式になります。

なぜ行列式を学ぶのでしょうか？　ひとつの理由は、行列式は行列が表す線形変換の体積拡大率を表すものとして利用されるからです。

参考：なぜ行列式を学ぶ？面積・体積との一致、ヤコビアンへの応用

もうひとつの理由は、行列が逆行列を持つかどうかの判定です。より具体的には、固有値・固有ベクトルを求めるときに、行列式の考え方が自然に登場することを紹介します。

固有値、固有ベクトルとは
固有値の求め方：固有多項式
こちらもおすすめ

固有値、固有ベクトルとは

固有値と固有ベクトルは、線形代数学の大きなテーマのひとつです。このサイトでも、数々の応用を紹介してきました。

参考：なぜ線形代数を学ぶ？ Googleのページランクに使われている固有値・固有ベクトルの考え方

参考：なぜ線形代数を学ぶか：人々の移動予測とマルコフ過程

参考：線形微分方程式の解の安定性は「固有値」を調べればわかる

参考：線形常微分方程式を行列で解く：行列の指数関数を解説

何らかの現象を数理モデル（線形モデル）として表すと、\(Ax\)と行列で表されます。インプット\(x\)に対して、その結果が\(Ax\)で表されるものです。しかし、行列のサイズが大きくなるほど、\(Ax\)の計算は複雑です。

ただし、仮に\(Ax = 2x\)という関係が成り立つ特殊な\(x\)が存在すれば、その\(x\)に関する計算はとても簡単になります。\(x\)に\(A\)をかけるということが、単に\(2\)倍するだけで良くなるわけですから。\(A\)を何回もかけることも簡単です、\(A^3 x = 2^3 x\)。この倍率\(2\)が固有値、行列の計算を簡単にする\(x\)が固有ベクトルです。一般的に定義しましょう。

\(A\)を\(N\times N\)の正方行列、\(\lambda\)を複素数、\(x \in \mathbb{R}^N\)として、

\[ \begin{aligned}Ax = \lambda x\end{aligned} \]

を満たす0でないベクトル\(x\)が存在する時、\(\lambda\)を固有値（eigenvalue）、\(x\)を\(\lambda\)に対応する固有ベクトル（eigenvector）と言います。

\(A\)は行列（線形写像）なので、\(x=0\)は常に\(Ax = \lambda x\)を満たしています。しかしそれはつまらないので、当たり前ではない\(x\)を探すわけです。

非常に簡単な例で、固有値と固有ベクトルを求めてみましょう。

対角行列\( A=\begin{pmatrix} 2& 0\\0 & 3 \end{pmatrix} \)を考えてみます。固有値や固有ベクトルがどんなものか求められますか？

\(Ax\)を計算してみると、\((2x_1,3x_2)\)です。これは2つの成分に分解できます。仮に\(x_2=0\)ならば、\(Ax =2 x\)が成立していますし、\(x_1=0\)ならば\(Ax=3x\)が成立しています。よって、固有値\(2\)に対応する固有ベクトルは\((1,0)\)、固有値\(3\)に対応する固有ベクトルは\((0,1)\)です。

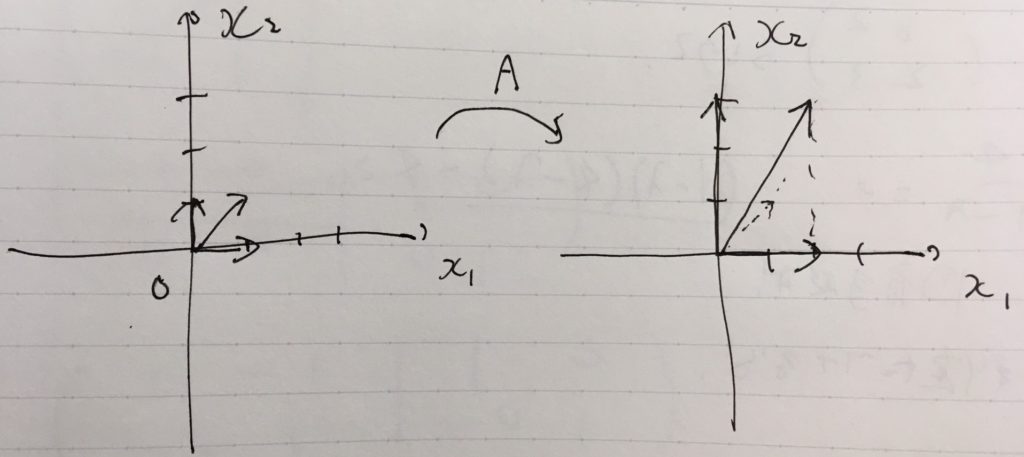
固有ベクトルは、変換\(A\)によって向きを変えないベクトルです。例えば、\((1,1)\)は固有ベクトルではありません。\(Ax=(2,3)\)で、右辺はどうやっても\((1,1)\)の定数倍になりません。一方で、固有ベクトルは\(A(1,0)=(2,0)=2(1,0)\)と向きを変えていないのです。

ある固有値に対して、固有ベクトルは無数に存在します。例えば、\((-1,0)\)も固有値\(2\)に対応する固有ベクトルです。なぜなら、\(A(-1,0)=(-2,0)=2(-1,0)\)なので。ただし、\((-1,0)=-1(1,0)\)と定数倍の差があるのみで、定めている方向は同じです。（固有ベクトルのなす空間：固有空間が1次元）

今回は、対角行列\( A=\begin{pmatrix} 2& 0\\0 & 3 \end{pmatrix} \)を、2つの方向\((1,0),(0,1)\)に分解して捉えました。固有値と固有ベクトルを求めることは、行列計算がシンプルになる方向を探すことにつながっています。（行列をシンプルな形＝対角行列に変形する：対角化の手段です）

固有値の求め方：固有多項式

別の例を考えてみましょう。\( B=\begin{pmatrix} 1& 2\\2 & 4 \end{pmatrix} \)の固有値と固有ベクトルを求めたいとします。

\(Bx=\lambda x\)を満たす\(\lambda, x\)を探すわけですが……対角行列のように単純ではありません。

そこで、この条件を次のように言い換えてみましょう。\(\lambda x =\lambda I x\)と単位行列を出すことで、\((\lambda I – B)x=0\)の非自明な解\(x\)を求めよ、という問題に変わります。

参考：可逆な行列（正則行列）とは？例と同値な条件

もし\(\lambda I – B\)が可逆ならば、\(x=0\)のみしか解がありません。つまり、非自明な解を持つための条件は、行列が可逆でないこと、ランクが落ちていることと言い換えられます。

\(\lambda I -B = \begin{pmatrix} \lambda -1& -2\\-2 & \lambda -4 \end{pmatrix} \)が可逆でなくなる\(\lambda\)を求めましょう。つまり、ランクが落ちているのはどういう\(\lambda\)なのかを調べるため、この行列を基本変形していきます。

まず、\(\lambda =1\)のときは、フルランクなので求める条件に当てはまりません。そこで、\(\lambda -1 \neq 0\)とします。

\(\begin{pmatrix} \lambda -1& -2\\-2 & \lambda -4 \end{pmatrix}\sim \begin{pmatrix} \lambda -1& -2\\-2 (\lambda -1)&( \lambda -4) (\lambda -1)\end{pmatrix} \)

\(\begin{pmatrix} \lambda -1& -2\\-2 (\lambda -1)& \lambda -4 (\lambda -1)\end{pmatrix}\sim \begin{pmatrix} \lambda -1& -2\\0& (\lambda -4 )(\lambda -1) – 4\end{pmatrix} \)

ここでランクが落ちるのは、 \((\lambda -4 )(\lambda -1) – 4=0\)となるときです。これは\(\lambda\)に関する2次方程式であり、2つの固有値が求まり、それによって固有ベクトルが求まります。（固有値は0と5、対応する固有ベクトルは\((2,-1),(1,2)\)）

\(Bx=\lambda x\)を満たす固有値を求めるという問題が、 2次方程式\((\lambda -4 )(\lambda -1) – 4=0\)の解を探せという問題に言い換えられました。この固有値を求めるための方程式\(p(\lambda)\)を、固有多項式（characteristic polynomial）と呼びます。

しかし、ランクが落ちる条件から固有多項式を探すのは面倒です。固有多項式を求める計算は、行列式によって表すと簡単になります。

\[ \begin{aligned}p(\lambda):= \det (\lambda I -A) \end{aligned} \]

を固有多項式と定義します。

\(\det\)は行列の行列式と呼ばれる数で、行列の成分の積と和によって定まっています。例えば、\(A=\begin{pmatrix} a& b\\c & d \end{pmatrix} \)に対しては、\(\det A = ad -bc\)です。行列式が0に等しいことは、可逆でないこと、ランクが落ちていることと同値であるように定められています。（行列式については別記事で紹介予定）

これを使えば、固有多項式の求め方は機械的になります。

\[\begin{aligned} p(\lambda )&= \det (\lambda I -B) \\&= \det (\begin{pmatrix} \lambda -1& -2\\-2 & \lambda -4 \end{pmatrix} )\\&=(\lambda -4 )(\lambda -1) – 4\end{aligned} \]

この定義によれば、\(N\times N\)行列の固有多項式の最高次の項は\(\lambda ^N\)であり、\(N\)次の多項式となります。

代数学の基本定理より、\(N\)次方程式には複素数の範囲で\(N\)個解が存在します。つまり、\(N\)次の行列には（重複込みで）必ず\(N\)個の固有値が存在するわけです。

さらには、ある行列の行列式は、その行列の固有値に等しい\(\det A = \lambda _1 \cdots \lambda_N\)という関係があります。

固有値を\(\lambda_1,\dots,\lambda _N\)と表すことにしましょう。\(p(\lambda_1)=\cdots=p(\lambda_N)=0\)なので、多項式に関する因数定理（剰余の定理）により、\(p(\lambda)= (\lambda-\lambda_1)\cdots (\lambda -\lambda _N)\)と因数分解できます。

ここで\(\lambda=0\)とすると、\(\det (-A) = (-\lambda_1)\cdots (-\lambda _N)\)です。行列式の性質より、1つの列から\(-1\)をくくりだすと\(-1\)倍されるので、\(\det (-A) = (-1)^N \det A\)となります。一方で右辺も\((-\lambda_1)\cdots (-\lambda _N)=(-1)^N \lambda _1 \cdots \lambda_N\)です。よって、\(\det A = \lambda _1 \cdots \lambda_N\)がわかりました。

固有値は、固有ベクトル方向への行列の拡大率です。行列式とは、各固有ベクトル方向への拡大率の積で表される量であることがわかりました。もし固有値のひとつが0ならば行列式は0、行列は可逆ではありません。逆に、行列式が0ならば最低1つは0の固有値があるわけです。可逆な行列ならば、すべての固有値は0ではないとも言えます。

今回は、行列式を学ぶ理由として、固有値・固有ベクトルの求め方を紹介してきました。線形方程式を解くことではなく、線形方程式が解けるかどうかを判定するためならば、基本変形によってチェックするよりも、（同じことですが）行列式による方が単純です。

固有値を求めるために必要な固有方程式は、行列式によって定義されます。行列式は固有値の積という関係性があり、両者は行列の変換倍率を調べるのに役立つということが、なんとなく感じられたでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。