どうも、木村(@kimu3_slime)です。
今回は、人々の移動の確率的なシミュレーションにおいて、線形代数学・確率論の考え方(マルコフ過程)が役立っていることを紹介します。
人々の移動予測
人々がたくさん歩いている都市部や駅前をイメージしてみてください。混雑してて、歩きにくいですよね。お店や施設をそこで運営する立場からしたら、人々が気軽に回遊して、利用・消費してほしいものです。
どういう場所に人が集まりやすいのか。それを数学(線形代数学・確率論)を使ってモデル化し、シミュレーションした論文があります。
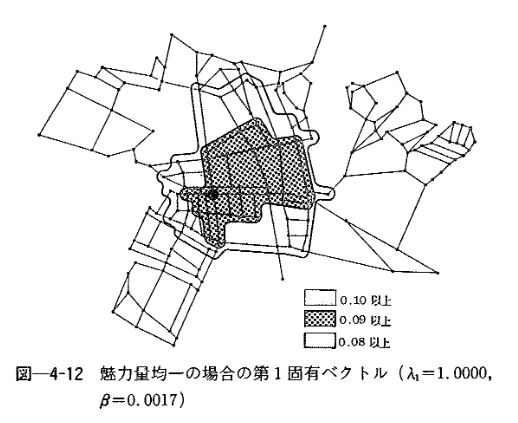
画像引用:推移確率行列を用いた歩行者流動の分析手法に関する研究
ある地域が、滞在する場所は点として、そこをつなぐ道は線として表されています。このような点と線の集まりをは、グラフと呼ばれるものです。
時間が経てば、人々は隣り合う点へ移動していくか、そのまま滞在を続けるかのいずれかでしょう。ここでは、人々が確率的に移動すると仮定しています。
例えば魅力的な場所ならば滞在する確率は高いでしょうし、歩きやすい道のつながる場所に比べれば、細い道のつながる場所への移動確率は低いでしょう。
こうした人々の移動の確率は、ひとつの行列(推移確率行列)として定式化されます。
かなりの時間が経つ、つまり何度も行列をかけていったときに、人々はどの場所にどれだけいることになるのか。それを計算して求めた結果が、上で引用した図のようになるのでしょう。
今回は、非常に簡単な例を使って、このモデル化の方法(マルコフ過程・マルコフ行列)を紹介していきます。
マルコフ過程、マルコフ行列とは
次の図のような人々の移動法則を考えてみましょう。
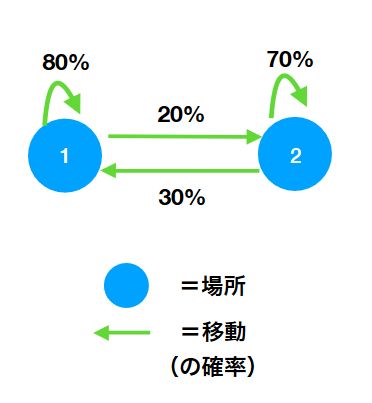
場所1と場所2があって、人々がそこにどれだけいるかという状態は\(u= (100,10)\)のように2次元のベクトルで表されます。例えば1時間毎に、矢印に書いてある確率で人々は移動または滞在するという変化が起こる。そんな状況を想定しています。
この確率的な移動は、1つの行列
\[ \begin{aligned} A = \begin{pmatrix} 0.8 & 0.3\\0.2 & 0.7 \end{pmatrix}\end{aligned} \]
によって表されます。最初は\(u_0\)という人々の分布から始まったとすると、\(Au_0 , A^2 u_0 ,\dots \)と人々は移動していくわけです。最終的にどんな状態になるか気になりますね。(予想できますか?)
この確率的な移動を表す行列は、マルコフ行列(Markov matrix)、または確率行列(stochastic matrix)と呼ばれます。移動によって人々がどこかへ消えてしまうことがないよう、人々はいずれかの隣り合う地点へ移動します。つまり、
- 行列のすべての成分が正(\(a_{ij} >0\))
- 行列の各列の成分の和が1となっている
行列が、マルコフ行列です。
一般に、時間とともに確率的に状態が変化していくようなプロセスは、確率過程(stochastic process)と呼ばれます。
今回考えている確率過程では、過去の移動履歴を参照せずに、次の移動先が決まります。このような確率過程を特にマルコフ過程(Markov chain)と呼びます。特に、取りうる状態が離散的なマルコフ過程をマルコフ連鎖(Markov chain)と呼びます。
現在の状態のみ参照するので、図における矢印は複雑になりすぎません(上で書いたような図を状態遷移図 という)。また、取りうる状態が有限個なので、行列、線形代数の言葉を使って分析できます。(より複雑な確率過程を考えたらこうはいかない)
さて、
\[ \begin{aligned} A = \begin{pmatrix} 0.8 & 0.3\\0.2 & 0.7 \end{pmatrix}\end{aligned} \]
によって定まる移動によって、人々の人口分布は最終的にどういう状態になるのでしょうか?
一般に、\(A u = u\)を満たす状態\(u\)は定常状態(steady state)と呼ばれます。これは固有値・固有ベクトルの枠組みで言えば、\(Au = \lambda u , \lambda =1\)、つまり\(1\)を固有値として持つ固有ベクトルとも言えますね。もし\(u\)が定常状態ならば、いくら\(A\)をかけても変化しないわけです。
簡単な計算によって、
\[ \begin{aligned} \begin{pmatrix} 0.8 & 0.3\\0.2 & 0.7 \end{pmatrix} \begin{pmatrix} 0.6\\0.4 \end{pmatrix}= \begin{pmatrix} 0.6\\0.4 \end{pmatrix}\end{aligned} \]
がわかります。定常状態を\(u_\infty \)と表すことにすれば、\(u_\infty = (0.6,0.4)\)ですね。
もう一方の固有値は\(0.5\)で、対応する固有ベクトルは\( (-1,1)\)です。
さてこのようにして定めた\(u_\infty \)は、適当な\(u_0\)の極限\(A ^k u_0 \to u_\infty (k \to \infty)\)となります。なぜでしょうか。
初期値を\(u_0 =(0.5,0.5)\)として計算してみましょう。これを固有ベクトルの線形結合で表すと計算しやすいです。
\[ \begin{aligned}u_0 = \begin{pmatrix} 0.5\\0.5 \end{pmatrix}=\begin{pmatrix} 0.6\\0.4 \end{pmatrix}+(0.1)\begin{pmatrix} -1\\1 \end{pmatrix}\end{aligned} \]
これによって、\(A^k u_0\)を計算していきましょう。固有ベクトルの性質より、
\[\begin{aligned} A u_0 &= A(\begin{pmatrix} 0.6\\0.4 \end{pmatrix}+(0.1)\begin{pmatrix} -1\\1 \end{pmatrix}) \\ &= 1\begin{pmatrix} 0.6\\0.4 \end{pmatrix}+(0.5)(0.1)\begin{pmatrix} -1\\1 \end{pmatrix}\end{aligned} \]
なので、固有値の部分だけがべき乗されていき、
\[\begin{aligned} A^k u_0 &= 1^k\begin{pmatrix} 0.6\\0.4 \end{pmatrix}+(0.5)^k(0.1)\begin{pmatrix} -1\\1 \end{pmatrix} \\&\to \begin{pmatrix} 0.6\\0.4 \end{pmatrix} =u_\infty \quad(\mathrm{as}\; k \to \infty)\end{aligned} \]
と、1以下の固有値(\(0.5\))に関する固有ベクトルが消え、固有値1に対応する\(u_\infty\)だけが残ります。
より一般の初期値であっても、その成分の合計が1ならば、(そういうベクトルを確率ベクトルという)
\[ \begin{aligned}u_0 = \begin{pmatrix} 1- \alpha\\ \alpha \end{pmatrix}=\begin{pmatrix} 0.6\\0.4 \end{pmatrix}+(\alpha -0.4)\begin{pmatrix} -1\\1 \end{pmatrix}\end{aligned} \]
同様の計算によって、\(A^k u_0 \to u_\infty\)です。
よって、最初に提示された図で示されたように人々が移動していくとすると、最初にいた人口がいくらであろうが、場所1の人口:場所2の人口=6:4になります。例えば、場所1が3000人なら場所2が2000人という関係に落ち着くわけですね。
今回の議論は、一般の(\(n\times n\))(成分が正の)マルコフ行列に適用できます。
マルコフ行列は固有値1を必ず持ち、他の固有値の絶対値は1以下となります。したがって、
\[\begin{aligned} A^k u_0 &= x_1 +c_2(\lambda_2)^k x_2+\cdots c_n (\lambda _n)^k x_n \\&\to x_1 \quad(\mathrm{as}\; k \to \infty)\end{aligned} \]
です。この展開は、より一般の行列(正の正方行列)に関する次の定理に支えられています。
ペロン・フロベニウスの定理
正方行列\(A\)の成分をすべて正とする。このとき、
\(A\)の固有値はすべて正。
そのうち最大のものを\(\lambda_{\max}\)とすると、それは単純固有値。(対応する固有空間が1次元)
\(\lambda_{\max}\)以外の固有値を\(\lambda\)とすると、\(|\lambda| < \lambda_{\max}\)
参考、証明は:齋藤「線型代数入門」p.217
今回は、人々の移動シミュレーションを例に、マルコフ過程、マルコフ行列を紹介しました。
その定常状態が固有問題として定式化されること、行列のべき乗の計算に固有ベクトルが役立つことが感じられたでしょうか。
今回は人口の移動の例を出しましたが、マルコフ過程は様々な確率的な推移法則を表すことができ、例えば待ち行列理論として応用されています。
また、Googleの検索順位付けの方法、ページランクにも応用されています。確率的な「移動」は、ウェブページ間のリンクを歩くネットサーフィンです。価値あるリンクの張られたページに対しては移動確率が高いという規則を考えて、定常状態として得られるのがページランクです。
参考:The PageRank Citation Ranking: Bringing Order to the Web (1999)
線形代数学の考え方が、確率的な移動の理論を通じて、広く役立っているのを感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社
売り上げランキング: 31,260
こちらもおすすめ
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方