どうも、木村(@kimu3_slime)です。
行列・線形代数を学び始めると、行列の積が「横×縦」であると知ることになります。
なぜそのような定義をするのでしょうか? 今回は、行列の積を変換の合成と見ることで、その理由のひとつを提示します。
行列を変換として見る
そもそも、行列とは何でしょうか。
数を縦横に並べたもので、連立方程式を解くのに都合が良い、でしょうか。それは間違いではありません。
しかし、行列にはベクトルや空間の変換という側面があります。すなわち、線形変換(linear transformation)とも呼ばれるのです。
変換とはどういうことか、説明します。
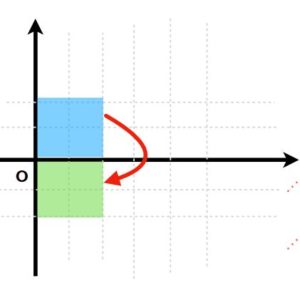
\(D:=[0,1]^2= \{(x,y)\in \mathbb{R}^2 \mid 0\leq x\leq1,0\leq y\leq1 \}\)で表される正方形の領域を考えましょう。
これを\(x\)軸につき反転させる変換を考えます。
つまり、\(x^{\prime}=x ,y^{\prime} =-y\)と変換することで、領域は
\[ \begin{aligned}D^{\prime}:= \{(x^{\prime},y^{\prime} )\in \mathbb{R}^2 \mid 0\leq x^{\prime}\leq1,-1\leq y^{\prime} \leq0 \}\end{aligned} \]
となりますね。
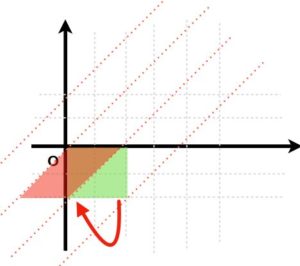
さらに、\(y\)軸方向に正方形をひし形へ変形させてみる変換、すなわちせん断(shear)を考えます。
つまり、\(x^{\prime\prime} = x^{\prime}+y^{\prime} , y^{\prime\prime}= y^{\prime} \)となる変換を考えると、領域は
\[ \begin{aligned}D^{\prime\prime}:= \{(x^{\prime\prime},y^{\prime\prime})\in \mathbb{R}^2 \mid -1\leq y^{\prime\prime}\leq0,x^{\prime\prime}-1\leq y^{\prime\prime}\leq x^{\prime\prime}\}\end{aligned} \]
となります。
行列を使って変換を表すと、見通しが良い
こうした変換を、行列の言葉を使って表してみましょう。
最初の変換\(x^{\prime}=x ,y^{\prime} =-y\)は、
\[ \begin{aligned}\begin{pmatrix} x^{\prime} \\ y^{\prime} \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}\end{aligned} \]
となり、続くせん断\(x^{\prime\prime} = x^{\prime}+y^{\prime} , y^{\prime\prime}= y^{\prime} \)は
\[ \begin{aligned}\begin{pmatrix} x^{\prime\prime} \\ y^{\prime\prime} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x^{\prime}\\ y^{\prime} \end{pmatrix}\end{aligned} \]
となります。
つまり、ここにおいて行列とは係数の略記です。一般に、線形変換\(x^{\prime}=a_{11}x+a_{12}y ,y^{\prime} =a_{21}x+a_{22}y\)は、
\[ \begin{aligned}\begin{pmatrix} x^{\prime} \\ y^{\prime} \end{pmatrix}=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}\end{aligned} \]
と行列で表せます。(と、表すことで行列を定義します)
ここで、行列の積を「横×縦」とする理由がわかります。
2つの変換を組み合わせたもの\((x,y)\mapsto(x^{\prime\prime},y^{\prime\prime})\)を考えてみましょう。
代入をすれば、\(x^{\prime\prime} = x^{\prime}+y^{\prime}=x-y \)、\(y^{\prime\prime} =y^{\prime}=-y \)となるわけですが、少し見通しが悪いです。
そこで、さきほどの行列の言葉で書かれたものを計算してみましょう。
\[\begin{aligned} \begin{pmatrix} x^{\prime\prime} \\ y^{\prime\prime} \end{pmatrix}&=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x^{\prime}\\ y^{\prime} \end{pmatrix} \\ &= \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}\\ &= \begin{pmatrix} 1 & -1 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}\\ &= \begin{pmatrix} x-y\\ -y \end{pmatrix} \end{aligned} \]
各変数ごとの変換と同様の結果が、行列計算によって統一的に得られています。
変数を(線形的に)2回変換するということは、本質的には行列の積の計算と同じ。
今回は単純な変数変換を考えましたが、より多くの複雑な変数変換を行えば、逐一代入するよりも、行列の言葉で扱う方が効率が良いでしょう。(例えば2変数でなく\(n\)変数の変換を考えるとか)
行列の積は、変換の合成と整合的
もう少し、関数・写像の言葉を使って整理してみましょう。
最初の変換を\(f((x,y))=A(x,y)\)、せん断を\(g((x^{\prime},y^{\prime}))=B(x^{\prime},y^{\prime})\)と表します。
この変換をあわせたものは、合成関数・合成写像\(h((x,y))=g\circ f((x,y))\)です。これは行列としては
\[\begin{aligned} h((x,y))&=g\circ f((x,y))=g(f(x,y))\\&=B(Ax) \end{aligned} \]
となるわけですが、行列の積は\(B(Ax)=(BA)x\)となるように定義されています。
つまり、逐次の変換(\(x\)に\(A\)を作用させ、その後\(B\)を作用させる)と、一度の変換(積\(BA\)を計算してから、\(x\)に作用させる)が同じ結果になるように定義されているわけです。
例えば\(2\times2\)行列なら、
\[\begin{aligned} B(A(x,y))&=\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} (\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}) \\ &= \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \begin{pmatrix} a_{11} x+ a_{12}y \\ a_{21}x + a_{22} y\end{pmatrix} \\ &= \begin{pmatrix} (b_{11}a_{11}+b_{12} a_{21} )x+ (b_{11}a_{12}+ b_{12}a_{22})y \\ (b_{21}a_{11} +b_{22}a_{21})x+(b_{21} a_{12}+b_{22} a_{22})y \end{pmatrix}\end{aligned} \]
\[\begin{aligned} (BA)(x,y)&=(\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}) \begin{pmatrix} x\\ y\end{pmatrix} \\ &= \begin{pmatrix} b_{11}a_{11}+b_{12} a_{21} & b_{11}a_{12}+ b_{12}a_{22} \\b_{21}a_{11} +b_{22}a_{21} & b_{21} a_{12}+b_{22} a_{22} \end{pmatrix} \begin{pmatrix} x\\ y\end{pmatrix}) \\ &= \begin{pmatrix} (b_{11}a_{11}+b_{12} a_{21} )x+ (b_{11}a_{12}+ b_{12}a_{22})y \\ (b_{21}a_{11} +b_{22}a_{21})x+(b_{21} a_{12}+b_{22} a_{22})y \end{pmatrix}\end{aligned} \]
と一致しているのがわかります。
逆に言えば、前者の結果\(B(A(x,y))\)と一致しているように、行列の積\(BA\)というものを定義したわけです。
ここまで来れば、行列の積を各成分の積ではなく、「行×列」の形で定義するのがむしろ自然であることに、納得できるのではないでしょうか。
行列の生みの親・ケイリーの発想
現在知られているような行列(matrix)の発想は、アーサー・ケイリー(Arthur Cayley)によるものと言われています。
高校数学、あるいは線形代数における、ケイリー・ハミルトンの定理でその名は知られているのではないでしょうか。
代数学の教科書「群論の味わい」によると、今回紹介したような2回の座標変換の規則を調べて、行列(とその積)を発見したそうです。
ケーリーと同様の道のりを辿ることで、行列の積の定義に習熟してもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
群論の味わい -置換群で解き明かすルービックキューブと15パズル-
共立出版
売り上げランキング: 455,168