どうも、木村(@kimu3_slime)です。
線形代数学で学ぶことになる、行列の行列式(determinant)。
値が0でなければ行列が正則になるといった性質があり、計算方法はよく学びます。一方で、値にどんな意味があるのかイメージしづらいのではないでしょうか。
今回は、行列式が面積・体積と一致すること、重積分の変数変換(ヤコビアン)に役立つことを紹介します。
行列式=面積・体積
2次の正方行列\(A=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \)に対し、行列式は\(\det A = ad -bc\)と定義されます。
ここで、行列\(A\)をベクトルの変換と見てみましょう。\(A\)の1列目のベクトルを\(a_1\)、2列目のベクトルを\(a_2\)とします。
基本ベクトル\(e_1=(1,0),e_2=(0,1)\)を\(A\)で変換すれば、\(Ae_1=(a,c)=a_1,Ae_2=(b,d)=a_2\)となります。
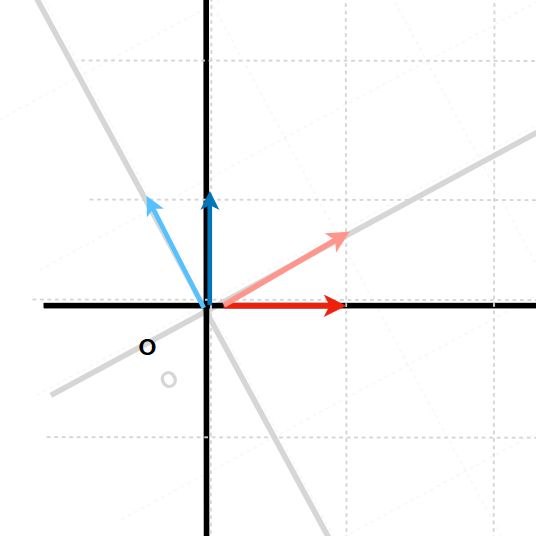
上の図では、濃い赤、青の矢印が基本ベクトルで、薄い赤、青の矢印が行列で変換された後のベクトルです。この図では、\(A\)は回転と拡大という変換をしています。
じつは、この変換による面積の拡大率が、\(A\)の行列式と一致するのです。計算してみましょう。変換後のベクトルがなす面積を\(S\)とします。(なす角によってはマイナスの値を取ります、いわゆる符号付き面積)
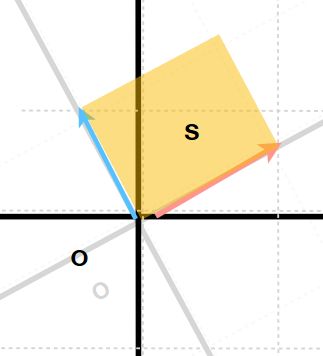
変換後のベクトル\(a_1,a_2\)がなす角を\(\theta\)とします。\(S\)は、これらが張る三角形の面積の2倍です。
\[ \begin{aligned}S&= |a_1||a_2|\sin \theta \\ &= |a_1||a_2| \sqrt{1 – \cos ^2 \theta}\\ &= |a_1||a_2| \sqrt{1 – \frac{(a_1 \cdot a_2 )^2}{|a_1|^2 |a_2|^2}} \\ &= \sqrt{|a_1|^2 |a_2|^2 – (a_1 \cdot a_2 )^2}\\ &= \sqrt{(a^2+c^2)(b^2+d^2) – (ab+cd)^2}\\ &= \sqrt{a^2d^2 – 2abcd +b^2c^2} \\ &= ad – bc \\ &= \det A \end{aligned} \]
基本ベクトルがなす正方形の面積は、1でした。変換\(A\)によって、その面積は\(ad-bc=\det A\)に変わります。つまり、\(\det A\)は、変換の拡大縮小率と言えますね。
拡大縮小率が0(\(\det A=0\))のとき、もともとあった平面は線分もしくは点につぶされてしまいます。行列が正則ではないとは、面を潰していることを幾何学的に意味することがわかりますね。
今回は2次元で說明しましたが、3次元のときも同様の性質が成り立ちます。
行列式の複数の定義
補足的な内容なので、ここは読み飛ばしても大丈夫です。
行列式の値が(行列の成分のベクトルがなす平行体の)体積の値となるのは、偶然ではなく必然です。
\(A\)を\(n\)次正方行列とします。置換を用いた行列式の定義は、
\[ \begin{aligned}\det A =\sum _{\sigma \in S_n} \prod _{1\leq i \leq n} \text{sgn}(\sigma) a_{i \sigma(i)}\end{aligned} \]
でした。\(\sigma\)は置換、sgnはその符号を意味しています。
この行列式を、行列の各列ベクトル\(a_1,\dots,a_n\)を変数とする関数\(f\)として見てみます。
このとき、\(f\)は次の2つの性質を持っています。
- 多重線形性(各変数について、関数が線形)
- 交代性(変数の順序を入れ替えると、値は同じままその入れ替えに応じた符号がかかる)
逆に、上記の2つの性質をもつ関数は、(定数倍を除いて)行列式に限ることが知られています。
参考:齋藤 線型代数入門 3章 定理2.6 p.81
そして、体積という関数(各ベクトルを変数とし、それらが張る平行体の体積を返す関数)もまた、多重線形性と交代性を持ちます。なので、これが(置換を用いた)行列式とも値が一致するわけです。
行列式(そして体積)の多重線形性と交代性は、行列式という関数を特徴づけています。
そしてこの性質があるからこそ、いわゆる「余因子展開」で、複雑な行列の行列式を簡単な行列式の計算に帰着できるのです。
また今回は、面積や体積を2-3次元に限って考えました。しかし、より高次元の体積を考えることができるようになっています。
\(n\)個のベクトル\(a_1,\dots,a_n\)のなす平行体の体積を、\(v(A)=\det A\)と定義してあげれば良いのです。低次元の現象から性質だけ取り出し、その性質を用いて高次元の場合を定義する一般化は、数学で広く行われています。
ヤコビアン=体積の変換倍率
話を換えて、行列式=変換倍率という観点が、重積分の計算に役立つことを紹介します。
高校で習う1次元の積分では、置換積分と呼ばれるテクニックがありました。
\(x=g(t)\)と置換するとき、
\[ \begin{aligned}\int_a ^b f(x)dx = \int _\alpha ^\beta f(g(t)) \frac{dg}{dt} dt\end{aligned} \]
となります。ここでの\(\frac{dg}{dt} \)が、まさに変換\(g\)の変換倍率なのです。
そして置換積分は、高次元では変数変換と呼ばれ、次のように表されます。(変換\(g\)には一定の条件つきで)
\[ \begin{aligned}\int_B f(x)dx = \int _A f(g(u)) |\det J_g (u)| du\end{aligned} \]
\[ \begin{aligned}J_g = \begin{pmatrix} \frac{\partial g_1}{\partial x_1} & \cdots & \frac{\partial g_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial g_n}{\partial x_1} & \cdots & \frac{\partial g_n}{\partial x_n} \\ \end{pmatrix} \end{aligned} \]
です。
関数\(g\)の一回偏微分を並べた行列\(J_g\)をヤコビ行列、その行列式をヤコビ行列式、またはヤコビアン(Jacobian)と呼びます。
一般に変数変換は線形(行列で表される)とは限らないのですが、積分の値を考えるにあたり必要なのは、各点での一回偏微分の値のみ。それより高次の無限小は影響してきません。
参考:杉浦 解析入門 Ⅱ7章 定理4.5 p.110
簡単で有名な変換は、曲座標変換です。2次元で考えてみましょう。
\(x=r\cos \theta,y= r \sin \theta\)となる変換\(g\)を考えます。このとき、ヤコビ行列は
\[ \begin{aligned}J_g = \begin{pmatrix} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos \theta \\ \end{pmatrix} \end{aligned} \]
なので、ヤコビアンは
\[ \begin{aligned}\det J_g =r \cos ^2\theta+r\sin^2\theta=r\end{aligned} \]
となります。
画像引用:polar graph,Mets501 – Wikipedia
実際、極座標は直交座標に比べて、原点から遠くでの面積が拡大されています。その拡大率が、\(r\)倍になっているというわけです。
大学初年度の線形代数の授業では、(置換による)抽象的な行列式の定義が与えられ、その性質を用いて行列式を計算する……そんな印象があります。
そこで今回は、行列式は行列変換による体積の拡大率であること、その実例として重積分の変数変換には行列式が登場することを紹介しました。
変数変換の例で見たように、非線形な関数・変換を対象にしていても、そのふるまいはそれを線形化した関数、すなわち行列によって分析できることがあります。
非線形の解くのが難しい問題を、線形、すなわち行列の問題にして解ける場合がある。そんなときに、行列、行列式、もとい線形代数学の理論が役立つことが、少しでも伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。